6. Интегрирование рациональных дробей

Дробно-рациональной алгебраической функцией называется функция вида , где P_n(x) и Q_m(х) многочлены степени n и m соответственно.

Если n ≥ m, то имеем неправильную дробно-рациональную функцию, например,

Если n < m, то имеем правильную дробно-рациональную функцию.

Например,

Утверждение 1. Любую неправильную дробно-рациональную функцию можно представить как сумму многочлена (целая часть) и правильной дробно-рациональной функции.

Пример.

Делим многочлен на многочлен

Таким образом, интегрирование неправильной дробно-рациональной функции сводится к интегрированию целого многочлена и правильной дроби.

Утверждение 2. Любой многочлен с действительными коэффициентами можно разложить на произведение множителей вида: .

Утверждение 3. Многочлен вида с целыми коэффициентами может иметь рациональный корень вида , где р - делители свободного члена , q – делители коэффициента старшего члена .

Пример. Найти рациональные корни многочлена

Решение: Делители 3:

Делители 4:

Возьмем

Следовательно - корень многочлена и многочлен без остатка разделится на

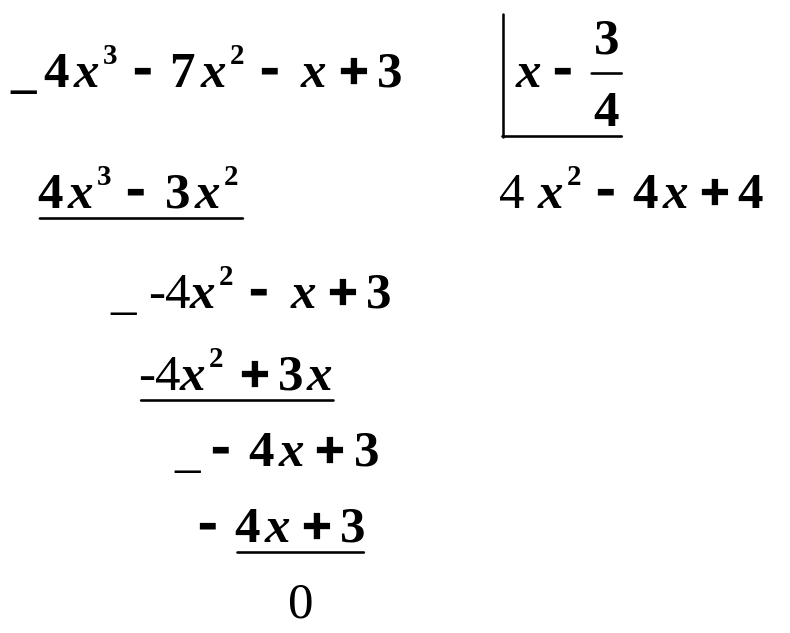
Многочлен можно представить в виде произведения двух множителей

Второй множитель не имеет рациональных корней.

Интегрирование простейших правильных дробно-рациональных функций

1)

2)

3) , квадратный трехчлен не раскладывается на множители (D < 0)

- решение рассмотрено в пункте 5 (стр. 15).

4)

Интеграл этого вида находим, используя справочник (Г.Б. Двайт. Таблицы интегралов «Наука» Москва 1973 г.).

Утверждение 4. Любую правильную дробно-рациональную функцию можно единственным способом разложить на сумму простейших правильных дробей указанных видов.

Алгоритм интегрирования правильных дробно-рациональных функций

1) Разложим знаменатель на множители вида

2) Разложим дробь на сумму простейших дробей, используя таблицу (на числитель не обращаем внимание). А, В,… - неизвестные коэффициенты.

№	Вид множителя в знаменателе	Вид простейшей дроби, соответствующей данному множителю
1
2
3
4
5

3) Полученную сумму приводим к общему знаменателю.

4) Приравниваем числители начальной дроби и полученной после приведения к общему знаменателю. Находим неопределенные коэффициенты А, В,...

5) Интегрируем полученную сумму дробей.

Пример.

1) Разложим знаменатель на множители. Найдем корни многочлена : делители 9: ±1; ±3; ±9 (p)

делители 2: ±1; ±2; (q)

Перебираем варианты дробей . Но корни по виду коэффициентов в многочлене.

- корень многочлена. Разделим на

Множитель - разложим по формуле

Итак,

2) Разложим дробь на сумму простейших дробей, пользуясь таблицей на стр. 20.

3) Приведем к общему знаменателю полученную сумму

4) Приравниваем числители

А, В, С можно найти, подставляя в полученное равенство «удобные» значения х (последовательно приравниваем к 0 скобки (х – 3) и (2х – 1))

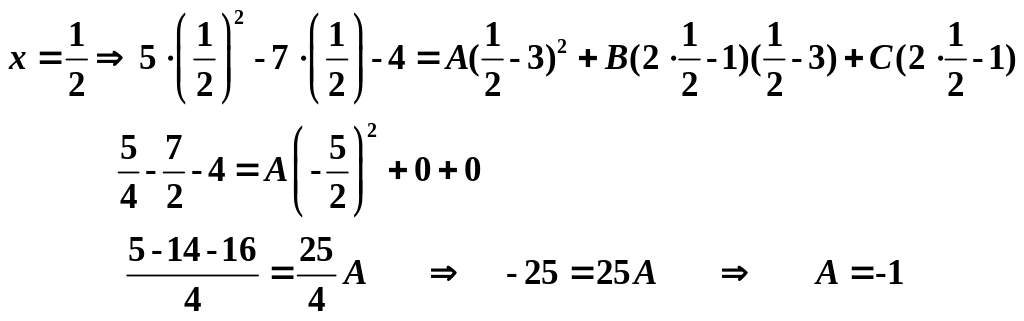
Произвольно возьмем:

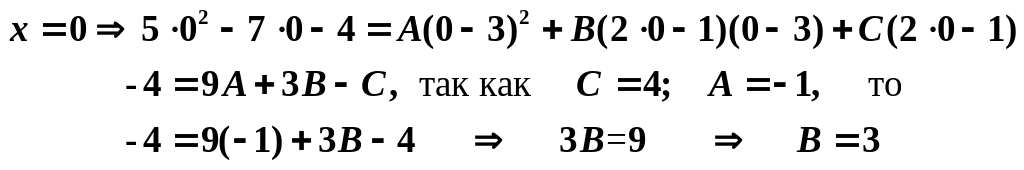
Получим

5) Интегрируем