2.3.1. Режим симметричной нагрузки

Рисунок 43. Электрическая схема при симметричной нагрузке

Для простоты построения векторных диаграмм рассмотрим случай, когда нагрузка носит чисто активный характер (рис. 43). Если характер нагрузки будет отличаться от чисто активного, то все выкладки остаются прежними, а векторные диаграммы токов поворачиваются на угол, равный углу сдвига по фазе между одноименными фазными токами и напряжениями.

Согласно определению при симметричной нагрузке и при чисто активном характере должно выполняться условие:

_.

Тогда согласно условию (4.3) фазные токи будут также равны по величине:

_.

Линейные токи можно определить, построив векторные диаграммы токов согласно системе уравнений (4.5).

Векторную диаграмму рис. 44. строим в следующем порядке:

1. Строим равносторонний треугольник линейных напряжений.

2. Строим вектора фазных токов _. Эти вектора совпадают по фаза с одноименными фазными напряжениями.

3. Строим вектора линейных токов согласно системе уравнений (5). Для построения вектора линейного тока из конца вектора тока 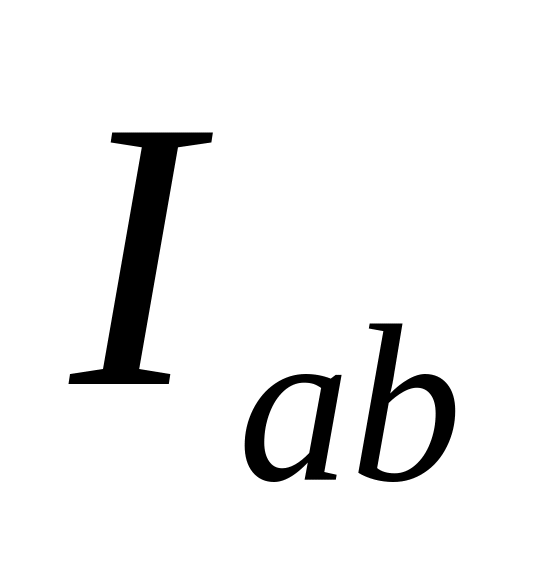строим вектор , равный по величине вектору тока , но имеющий обратное направление. Вектор тока проводим из начала вектора тока в конец вектора ( ). Аналогично строим вектора линейных токов и . На векторной диаграмме треугольники являются равнобедренными т.к. Из треугольника следует, что:

I_a=2I_abcos30^o= I_ab

Аналогично получается из треугольников ,что линейные токи будут в корень из трех раз больше фазных токов. Таким образом, линейные токи при симметричной нагрузке равны по величине и в корень из трех раз больше фазных токов.

_{, (4.7)}

Рисунок 44. Векторные диаграммы токов и напряжений

При симметричной нагрузке

2.3.2. Режим изменения тока одной фазы

Рассмотрим режим работы трехфазной цепи, соединенной по схеме треугольник при изменении величины сопротивления одной фазы. Допустим, сопротивление фазы BC уменьшили, т.е.:

_.

Тогда согласно уравнению (4.3) точки и останутся неизменными, а ток фазы увеличится:

_.

Для определения линейных токов строим векторные диаграммы токов и напряжений аналогично симметричному режиму работы. Векторные диаграммы представлены на рис. 45.

Рисунок 45. Векторные диаграммы токов и напряжений

При изменении тока одной фазы для случая

Сравнивая векторные диаграммы при симметричном режиме работы (рис. 44) и при изменении тока одной фазы (рис. 45) можно сделать следующие выводы:

1. При изменении тока в одной фазе токи в двух других фазах не изменяются (в нашем случае и ).

2. При увеличении тока одной фазы, токи в линейных проводах, примыкающих к этой фазе, также увеличиваются (в нашем случае токи и ).

3. Ток в третьем линейном проводе не изменяется (в нашем случае ток ).

2.3.3. Режим несимметричной нагрузки

Рассмотрим случай, когда нагрузка во всех фазах носит чисто активный характер, а между величинами сопротивлений фаз приемника справедливо следующее соотношение:

.

Рисунок 46. Векторные диаграммы токов и напряжений

При несимметричной нагрузке для случая

Тогда согласно системе уравнений (4.3) между величинами фазных токов будет справедливо следующее отношение:

Для определения линейных токов , , строим векторные диаграммы токов и напряжений. Векторные диаграммы строятся как при симметричной нагрузке. Векторная диаграмма представлена на рис. 46.

Сравнивая векторные диаграммы при симметричной нагрузке (рис. 44) и несимметричной нагрузке (рис. 46), можно сделать следующий вывод: при несимметричной нагрузке фазные и линейные токи, соответственно, не равны по величине и режим работы отдельных фаз не зависит друг от друга.