5.3.3. Реализация логических функций на элементах "и-не" и "или-не"

1. Выполнение функций на элементах "И-НЕ" можно проследить на рис. 5.3.5., а, б, в.

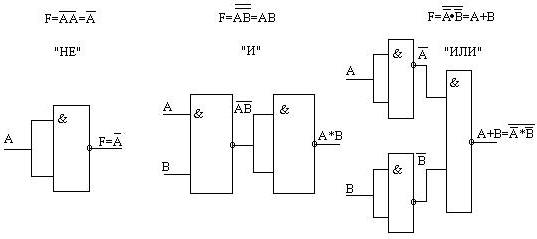
а) б) в)

Рис. 5.3.5. Выполнение функций F на элементах "И-НЕ"

2. Выполнение функций на элементах "ИЛИ-НЕ" на рис. 5.3.6, а, б, в.

а) б) в)

Рис. 5.3.6. Выполнение функций F на элементах "ИЛИ-НЕ"

Вышеприведенные упрощения производились на основе тождеств преимущественно интуитивно, что достаточно сложно. На практике для функций с числом переменных до пяти, шести наиболее удобным методом минимизации является применение диаграмм Вейча (или карт Карно).

5.4. Интегральные комбинационные схемы

Цифровые логические устройства подразделяются на два класса: комбинационные и последовательностные (или последовательные).

Комбинационные цифровые устройства реализуют различные преобразования двоичных цифровых сигналов на основе комбинационных логических функций. Выходные сигналы комбинационных устройств в любой момент времени однозначно определяются входными сигналами, имеющими место в этот момент времени.

К основным типам таких устройств относятся сумматоры, дешифраторы и шифраторы, преобразователи кодов, мультиплексоры и демультиплексоры, схемы сравнения двоичных чисел и др.

Ранее рассматривалось построение комбинационных логических устройств на основе элементов "И-НЕ" либо "ИЛИ-НЕ". В настоящее время благодаря развитию СИС и БИС широко применяются готовые комбинационные узлы, выполненные в одном корпусе. Это не только упрощает разработку схем, но и снижает стоимость оборудования, поэтому разработчик должен стремиться к наиболее широкому использованию имеющейся номенклатуры комбинационных ИМС для построения устройств.

Ниже будут рассмотрены наиболее распространенные комбинационные ИМС.

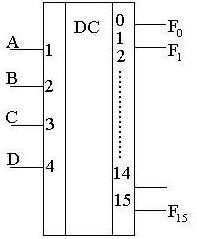
Дешифраторы (декодеры) – это такие комбинационные устройства, в которых каждой комбинации входных переменных соответствует логическая единица только на одном соответствующем входе

Таблица 5.4.1.

Рис. 5.4.1. Обозначение дешифратора

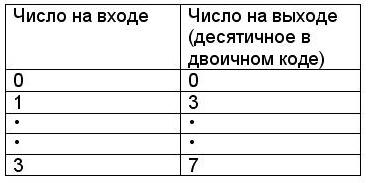
Таблица истинности дешифратора с четырьмя входами А, В, С, D приведена в таблице 5.4.1. Число выходов N=2ⁿ=16 – это максимальное значение при n=4, бывает, что N=10, 12. Сам дешифратор показан на рис.5. 4.1.

Дешифратор реализует следующие логические функции:

.

Дешифраторы широко применяются, как преобразователи двоичного кода в десятичный (к примеру для управления индикаторными приборами).

Шифраторы (кодеры) – устройства, выполняющие функции обратные тем, что выполняет дешифратор. Соответственно он имеет малое число выходов и большое входов. Обозначается он, как показано на рис. 5.4.2. на 3 выхода. При подаче сигнала на один из входов на его выходах появляется соответствующая комбинация логических единиц. Так, если А_о=1, а все остальные А_i, (где i от 0 до 7), равны нулю, то на выходе получаем код 000; если А₆=1, то код на выходе 110; если А₇=1, то 111. Таблица 5.4.2. даёт представление о всех возможных комбинациях на выходе при наличии логической единицы на каждом из входов.

Таблица 5.4.2.

Рис. 5.4.2. Обозначение шифратора.

Совокупность дешифратора с шифратором позволяет строить преобразователи кодов, как показано на рис. 5.4.3. Соединение дешифратора DС и шифратора СD (декодер и кодер) может быть самым различным. Работа определяется таблицей соответствий, пример которой приведен в таблице 5.4.3.

Рис. 5.4.3. Преобразователь кодов

Таблица 5.4.3.

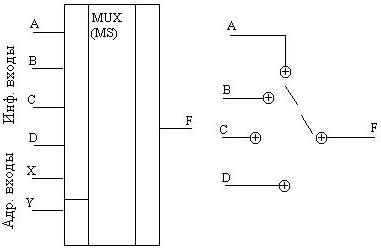
Мультиплексоры – это комбинационные устройства, в которых выход соединяется с одним из входов в зависимости от кода адреса, как показано на рис. 5.4.4., а) и б).

Таблица 5.4.5.

a) б)

Рис. 5.4.4. Обозначение мультиплексора

В соответствии с таблицей 5.4.5., если:

X, Y=00, тоF=A;

X,Y=01,F=B;

X, Y=10,F=C;

X, Y=11,F=D

Описывается работа приведенного мультиплексора следующим логическим уравнением:

;

Мультиплексоры применяются в устройствах отображения информации, в ЭВМ в микропроцессорных устройствах управления.

Кроме того, мультиплексоры могут работать и как логические устройства. К примеру, если надо реализовать функцию: F= Y+X , то можно поступить так (см. таб. 5.4.5.): возьмем А=0, D=0, а В=С=1, тогда используя уравнение мультиплексора получаем желаемый результат.

Демультиплексоры – это устройства, в которых значение функции F на входе подается на тот выход (А, В, С или D), адрес которого указан на адресных входах X, Y. Обозначение показано на рис. 5.4.5. Это устройство равнозначно дешифратору с дополнительным входом V=F, значение сигнала, на котором определяет значение сигнала на соответствующем выходе дешифратора, как это показано в таблице 5.4.6.

Таблица 5.4.6.

Рис. 5.4.5. Обозначение демультиплексора

Сумматоры – это устройства, предназначенные для выполнения операции сложения чисел, заданных в двоичном коде. Для установления правил сложения сравним сложение десятичных и двоичных чисел.

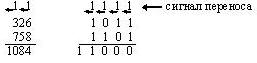
Правила сложения:

1) сложение выполняется поразрядно от младшего к старшему;

2) в младшем разряде вычисляется сумма младших разрядов слагаемых и , которая записывается либо однозначным числом (0+1=1), либо двузначным (1+1=10), где функция P называется переносом;

3) во всех последующих разрядах находится сумма разрядов слагаемых и , причем при к этой сумме добавляется единица переноса.

Результат сложения записывается в i-ом разряде в виде однозначного числа или двузначного . Вывод: в каждом i-ом разряде находится сумма чисел , и (если ), т.е. определяется и .

Одноразрядный сумматор показан на рис. 5.4.6., его таблица истинности приведена в табл. 5.4.7.

Таблица 5.4.7.

Рис. 5.4.6. Обозначение одноразрядного сумматора

Полусумматоры – устройства, отличающиеся от одноразрядного сумматора отсутствием входа сигнала переноса . Его обозначение показано на рис. 5.4.7, а работа отражена в табл. 5.4.8.

Таблица 5.4.8.

Рис. 5.4.7. Обозначение полусумматора

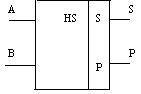
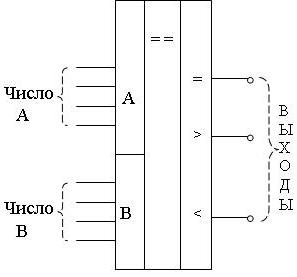
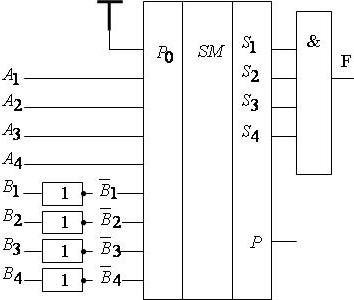
Цифровые схемы сравнения – устройства, которые формируют на соответствующих выходах "1" в зависимости от результатов сравнения двух чисел. Обозначение показано на рис. 5.4.8. На рис. 5.4.9. приведена схема сравнения, выполненная на базе многоразрядного сумматора и схемы "И".

Рис. 5.4.8. Обозначение устройства сравнения

Рис. 5.4.9. Схема сравнения, выполненная на базе многоразрядного сумматора и схемы "И"

Действительно, если А=В, то сумма =1

А0 1 0 1

1 0 1 0

S 1 1 1 1

Тогда:

Схема на рис. 5.4.9. может фиксировать и неравенство чисел А и В. Так, если А<В, то F=0 и P=0; если А=В, то F=1, P=0, а если А>В, то F=0, P=1, т.е. выдается сигнал переполнения.

Цифровая схема сравнения может рассматриваться, как цифровой аналог компаратора.