21. Энергия электрического поля, энергия заряженного конденсатора.

Предположим, что уединенный проводник, первоначально незаряженный, заряжают определенным количеством электричества q и его потенциал становится φ. Для того, чтобы зарядить проводник, необходимо затратить работу, которая и будет мерой энергии заряженного проводника. Чтобы увеличить заряд проводника на dq надо перенести этот заряд dq из ∞ на проводник. При этом затратится работа dA = dq (φ − φ∞) = dq∙φ = φ∙dq

Полная работа, которую надо затратить, чтобы зарядить проводник до заряда q, равна сумме элементарных работ dA, то есть ,так как q = C∙φ → dq = C∙dφ

Эта работа определяет энергию заряженного проводника

Учитывая, что С =q/φ, формула (7.1) преобразуется к видам и

Энергия заряженного конденсатора

Рассмотрим плоский конденсатор и найдем работу по перемещению заряда dq с одной пластины на другую( это работа источника) dA = dq (φ1 − φ2) = U∙dq

Полная работа зарядки конденсатора будет равна ,С = q/U − ёмкость

Конденсатора. Следовательно, энергия заряженного конденсатора будет иметь вид ,

Конденсаторы обладают способностью запасать в себе энергию.

22. Энергия электрического поля, плотность энергии электрического поля.

Преобразуем формулу энергии конденсатора так, чтобы туда вошла характеристика поля – напряженность

Учитывая, что ,, а S∙d = V − объём, занимаемый полем, получим

Энергию, приходящуюся на единицу объёма, называют объёмной плотностью энергии Зная плотность энергии поля в каждой точке, можно найти энергию любого поля, заключенного в любом объёме. ,− для однородного поля Е = const

23.Постоянный электрический ток, его характеристика.

Электрическим током называют направленное движение электрических зарядов

В металлах − это движение электронов проводимости, В растворах − это движение ионов,

В газах − это движение электронов и ионов одновременно, Если, например, к металлическому проводнику не приложено электрическое поле, свободные электроны движутся хаотично. Через любое сечение проводника в одну сторону проходит столько же электронов, сколько в противоположную. Поэтому результирующего переноса электронов через сечение нет, и электрический ток равен нулю.

У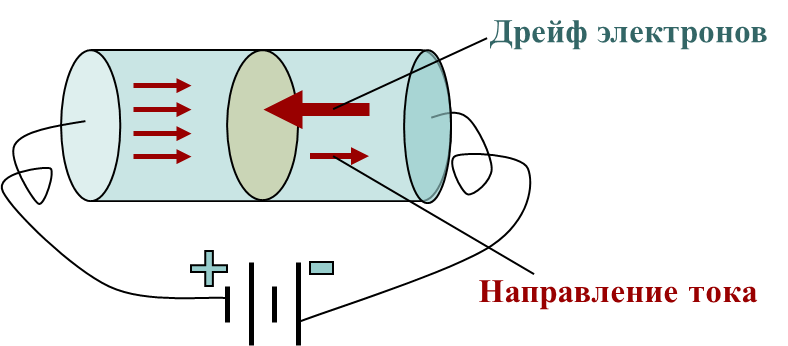 словились считать направление тока от + к -

За направление тока принято направление условного тока, совпадающее с электрическими силовыми линиями

Условия возникновения тока: наличие свободных электрических зарядов;

разность потенциалов на концах проводника;

поддержание разности потенциалов.

Для количественной характеристики электрического тока используют две основных величины:

плотность тока ( j ) и силу тока ( i )

Плотность тока − это физическая величина, равная величине заряда, проходящего через единицу поверхности в единицу времени

Сила тока − это физическая величина, равная величине заряда, проходящего через поперечное сечение проводника в единицу времени

связь силы тока и плотности тока i = j∙ds

Для любого сечения и, если вектор j не перпендикулярен ds это − интегральный ток. Если сила тока и плотность тока не изменяются во времени, то говорят, что по проводнику течет постоянный ток.