15.Электрическое поле в диэлектриках: поляризация диэлектриков, вектор поляризации, диэлектрическая восприимчивость вещества.

Диэлектрики – вещества, содержащие связанные друг с другом положительные и отрицательные заряды (свободные заряды отсутствуют). При внесении диэлектрика в электрическое поле, электрическое поле изменяется. Это происходит потому, что в первоначально незаряженных диэлектриках, помещенных в электрическое поле, появляются поляризационные заряды. Явление возникновения поляризационных электрических зарядов в диэлектрике, помещенном в электрическое поле, называется поляризацией

Поляризация диэлектриков

а) – неполяризованный диэлектрик (положительные и отрицательные заряды расположены равномерно по объему молекулы).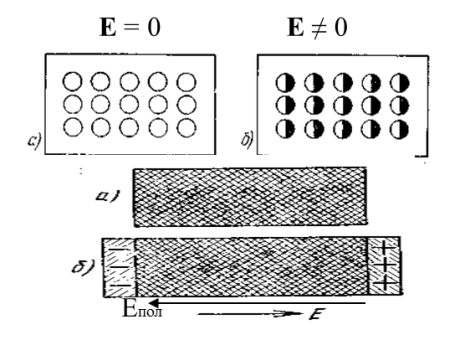

б) - поляризованный диэлектрик (заряды в каждой молекуле смещаются в противоположные стороны; при этом каждая молекула превращается в электрический диполь). При этом внутри диэлектрика все равно количество положительного заряда равно количеству отрицательного, но на одном конце поверхности возникает тонкий слой с некомпенсированным положительным зарядом, на другом – с некомпенсированным отрицательным. Возникнут поляризационные заряды Их нельзя отделить друг от друга, нельзя отделить от диэлектрика и располагаются они в тонком слое на поверхности диэлектрика.

Вектор поляризации

При поляризации диэлектрика каждая молекула становится электрическим диполем, а следовательно приобретает дипольный момент

где, − это физическая величина равная дипольному моменту единицы объема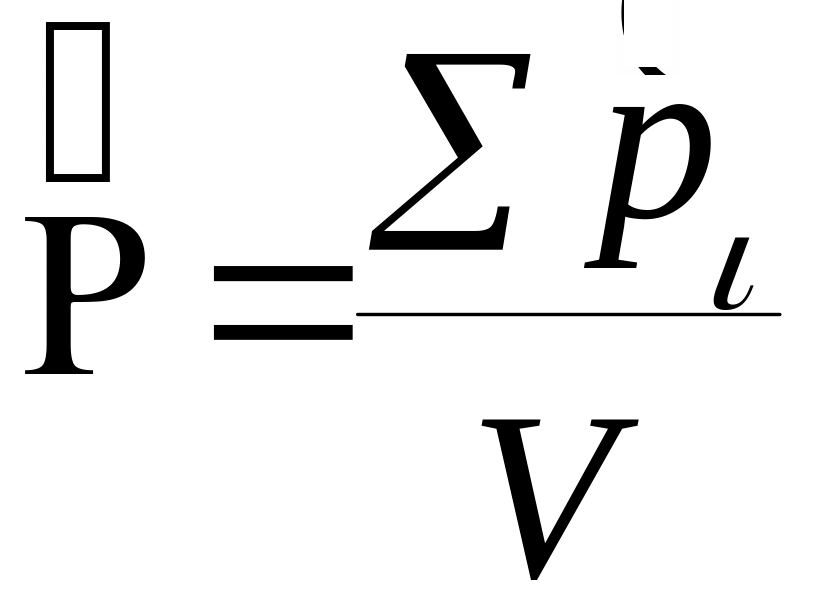

Поверхностная плотность поляризационных (связанных) зарядов равна нормальной составляющей вектора поляризации в данной точке поверхности:

Для изотропных диэлектриков, в которых поляризация не зависит от направления поля

− поле в диэлектрике. α − диэлектрическая восприимчивость вещества, величина безразмерная (всегда больше 0) Для большинства диэлектриков α составляет несколько единиц (например, для Н2О → α = 80, для спирта → α = 25)

В анизотропных диэлектриках и не совпадают.

16.Напряженность поля в диэлектрике.

П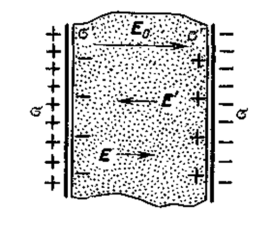 усть поле создается двумя бесконечно заряженными разноименными пластинами. Поле внутри пластин будет однородное и равно

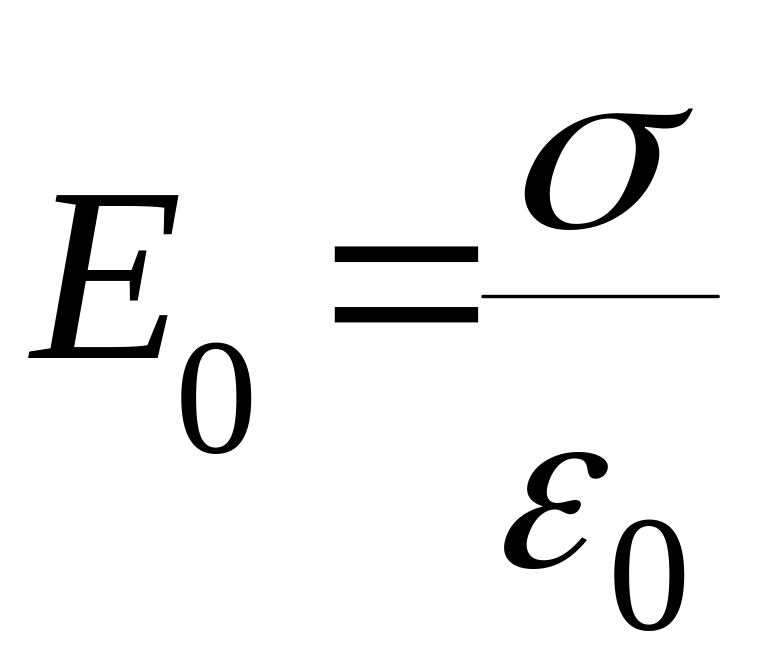
где  - поверхностная плотность зарядов на пластинах.

При внесении в электрическое поле изотропного диэлектрика появятся поляризационные заряды ( ) и соответственно дополнительное поле

Так как  , то не все поле компенсируется полем

Результирующее поле внутри диэлектрика будет равно. Учитывая, что в изотропном диэлектрике получим,

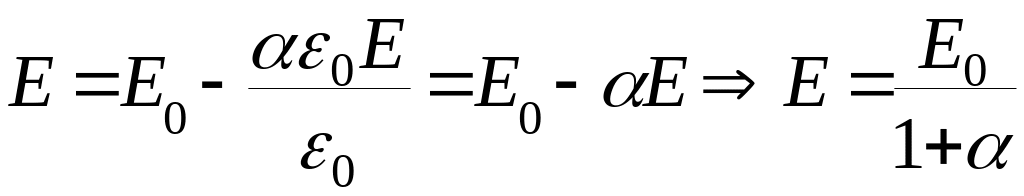
Таким образом, напряженность поля в диэлектрике равна

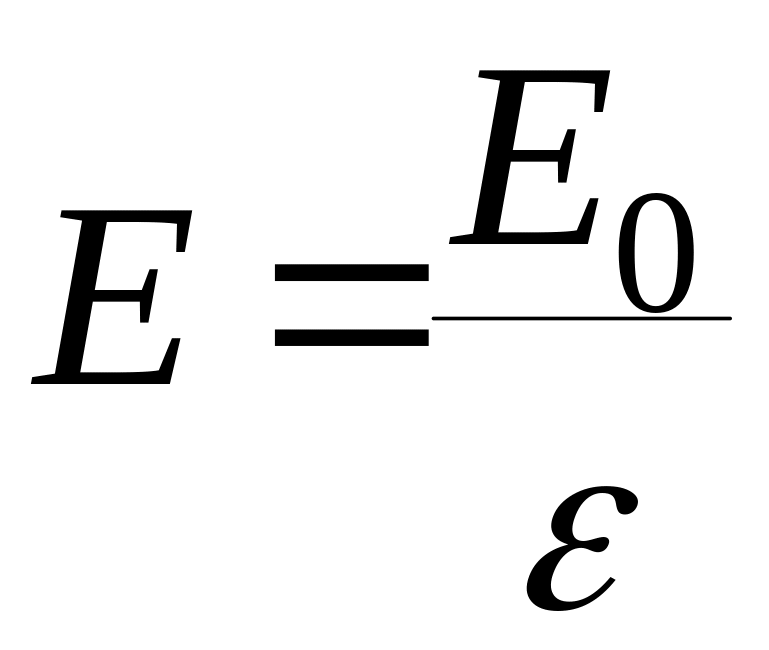
Поле в диэлектрике, помещенном в электрическое поле Е0, ослабляется в  раз.

Диэлектрическая проницаемость среды  показывает во сколько раз поле ослабляется диэлектриком и характеризует поляризационные свойства диэлектрика.

Сила взаимодействия точечных зарядов (закон Кулона) в диэлектрике запишется в виде: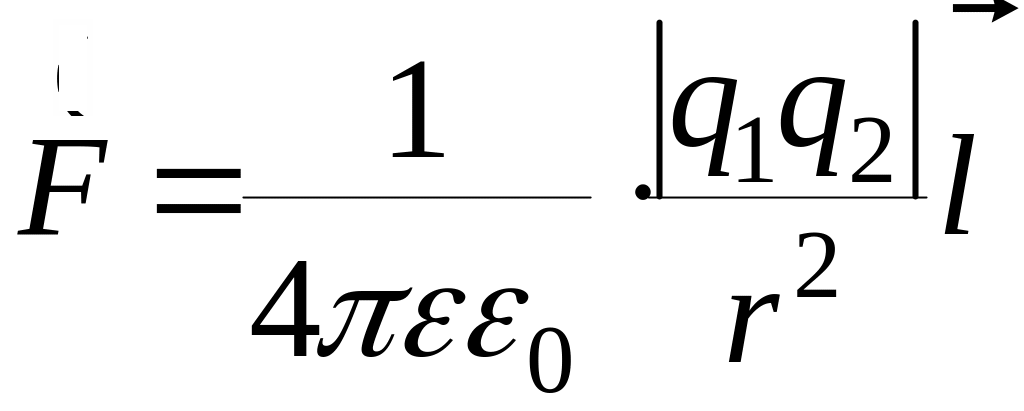

17.Вектор электрического смещения. Терема Гаусса для электростатического поля в диэлектрике.

Вектор напряженности переходя через границу диэлектриков с различными , скачкообразно изменяется и это создает неудобства при расчете электростатических полей.

Поэтому помимо вектора напряженности для характеристики поля ввели вектор электрического смещения

Для любого диэлектрика

Теорема Гаусса для электростатического поля в диэлектрике

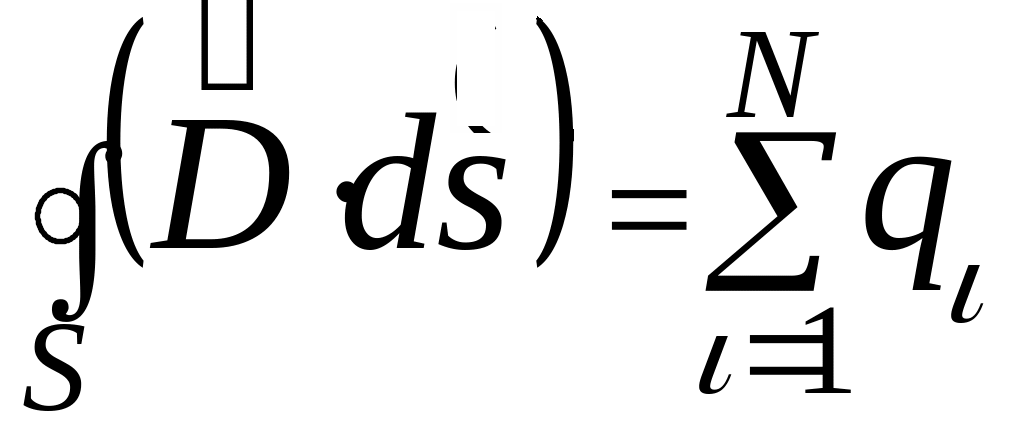Поток вектора электрического смещения сквозь замкнутую поверхность равен алгебраической сумме свободных зарядов, охваченных этой поверхностью

(независимо от того, есть поляризационные заряды или нет

В дифференциальной форме теорема Гаусса запишется в виде: div = ρ называют уравнением Пуассона.

Вектор удобен тем, что его можно рассчитать только по одним свободным зарядам, и по формуле можно найти