8.Применение теоремы Гаусса для расчета электростатических полей: поле равномерно заряженной бесконечной плоскости.

+σ – поверхностная плотность заряда

Найдем напряженность поля в точке А.

Исходя из этого выберем замкнутую поверхность, проходящую через точки А и В. Это может быть параллелепипед длиной 2х, четыре грани которого совпадают с

а две грани перпендикулярны , а может быть цилиндр, ось которого совпадает с

Найдем поток вектора напряженности через замкнутую поверхность (параллелепипед).

Ф = 4Фбок. + 2Фосн.

Фбок. = 0, т.к. боковой плоскости, или

S - часть заряженной плоскости внутри замкнутой

Поверхности.

Следовательно, полный поток через замкнутую поверхность равен Ф = 2Фосн = 2Е *Sосн

Приравняем этот поток по теореме Гаусса сумме зарядов, находящихся внутри параллелепипеда (это часть заряженной плоскости площадью S)

напряженность не зависит от положения точки А, то есть поле, создаваемое равномерно заряженной бесконечной плоскостью, однородное и направлено перпендикулярно плоскости.

9. Теорема Гаусса в дифференциальной форме.

Если подействовать им на вектор в виде скалярного произведения, то получится скаляр, называемый дивергенцией вектора:

Зная дивергенцию вектора в каждой точке пространства, можно вычислить поток этого вектора через любую замкнутую поверхность конечных размеров

Произведение дает мощность источников поля, заключенных в объеме dv

Запишем теорему Гаусса в интегральной форме

Следовательно, или выражают теорему Гаусса в дифференциальной форме. Они говорят о том, что электростатическое поле имеет источники – заряды.

10. Работа сил электростатического поля по перемещению заряда. Напряжение. Консервативность электростатических сил.

При перемещении зарядов в электростатическом поле совершается работа, поскольку на заряд в электростатическом поле действует кулоновская сила.

Предположим, что электрический заряд +q0 перемещается в поле точечного заряда +q из точки 1 в точку 2 вдоль произвольной траектории.

На заряд q0 будет действовать кулоновская сила

Эта сила будет совершать работу. Так как сила зависит от перемещения, то найдем сначала работу на бесконечно малом участке dl

,

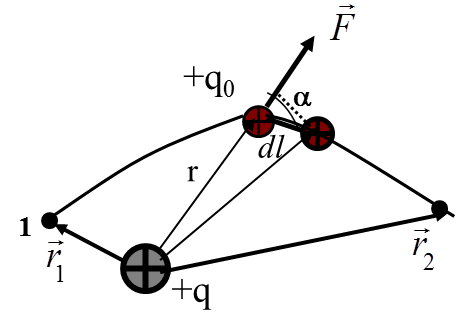Работа по перемещению заряда q0 из точки 1 в точку 2 будет равна

что работа не зависит от траектории перемещения, а определяется только начальным и конечным положением заряда q0.

Электростатическое поле точечного заряда является потенциальным, а электростатические силы – консервативными.

Исходя из этого работа кулоновских сил при перемещении заряда по замкнутому контуру будет равна нулю

11.Электростатически потенциал. Эквипотенциальные поверхности. Связь вектора напряженности и электрического потенциала. Принцип суперпозиции потенциалов.

Если поле создаётся непрерывным распределением зарядов, то потенциал определяется по формуле

Объединяя в электростатическом поле точки, обладающие одинаковым потенциалом, получим некоторые поверхности, которые называются эквипотенциальными .

Так как все точки эквипотенциальной поверхности имеют одинаковый потенциал, то перемещение вдоль нее не требует работы.

Это значит, что сила, действующая на заряд, все время перпендикулярна к перемещению.

С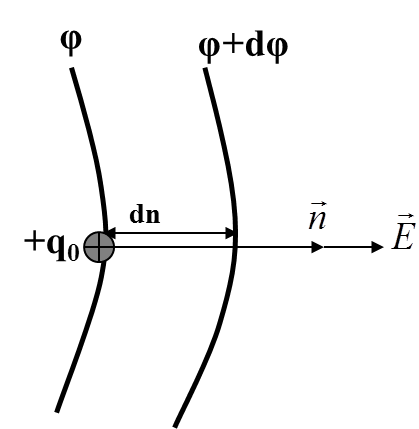 ледовательно, линии напряженности всегда перпендикулярны к эквипотенциальным линиям, так как

Связь между напряженностью и потенциалом

Рассмотрим две бесконечно близких эквипотенциальных поверхности 1 и 2

Потенциал поверхности 1  

Потенциал поверхности 2  d

Будем перемещать точечный заряд +q0

с поверхности 1 на поверхность 2 по кратчайшему пути (по нормали n).

в пределах dn const

Работа по перемещению заряда +q0 будет равна:

с одной стороны dA = q0 (1 - 2) = q0  – ( + d) = q0 d;

с другой стороны dA = q0 E dn

Приравнивая оба выражения для работы, получим

q0 E dn = − q0 d