6.Напряженность поля, создаваемого бесконечно длинной равномерно заряженной нитью.

Если одноименных точечных зарядов очень много и они очень близко расположены друг от друга, то расстояние между соседними зарядами практически не влияет на вычисление напряженности поля. В этом случае говорят заряд распределен непрерывно. Такое распределение зарядов характеризуется плотностью заряда. В случае равномерного распределения заряда по длине, как в данном случае, характеристикой является линейная плотность заряда 

Рассмотрим равномерно заряженную бесконечно длинную нить с линейной плотностью +τ

Найдем напряженность поля в т. А, которая лежит на перпендикуляре к нити на расстоянии а от нити

Применим тот же метод разделения распределенного заряда на элементарные заряды dq (метод дифференцирования), который мы применяли для вычисления силы взаимодействия заряженных тел.

1.Выбираем систему отсчета (ось y параллельна нити, ось x совпадает с перпендикуляром, начало отсчета - с точкой А).

2. Разбиваем заряженную нить на элементарные участки заряд которых

3. Определяем направление и величину напряженности поля создаваемого участками dq

4. По принципу суперпозиции находим напряженность поля, создаваемого всей заряженной нитью

Так как вектора от различных элементов будут иметь различное направление, суммирование надо вести по составляющим этих векторов

Разложим вектор на составляющие и

где

Чтобы проинтегрировать это выражение, нужно привести его к одной переменной, например к α

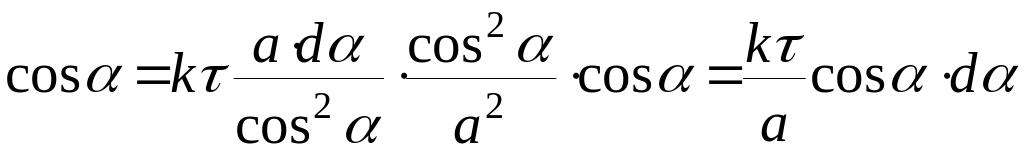
Подставив это выражение под интеграл

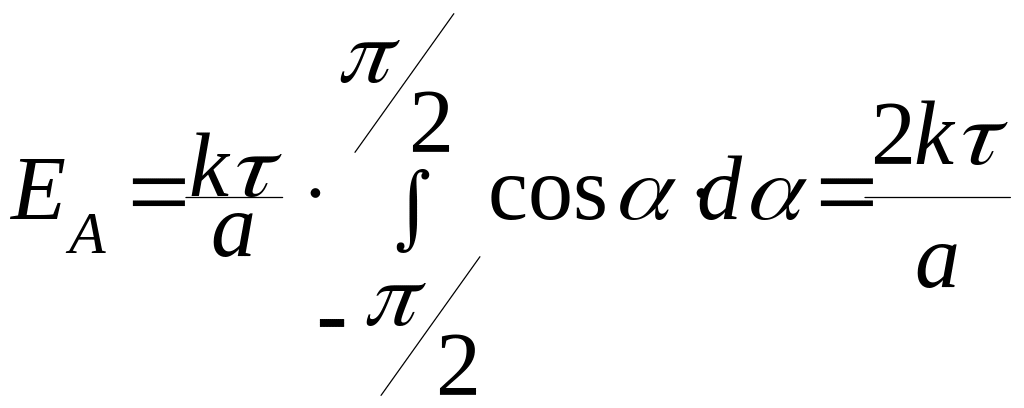
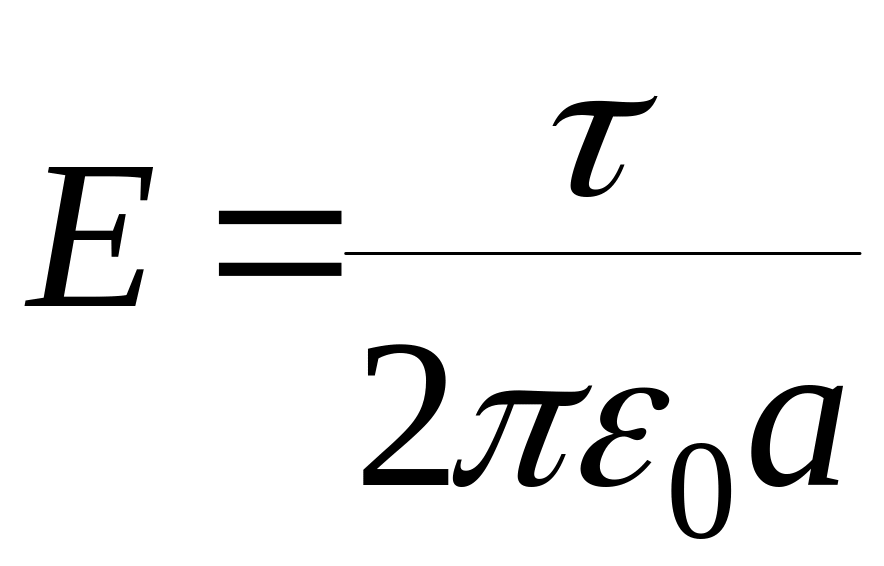
определяет напряженность поля, создаваемого бесконечной равномерно заряженной нитью на расстоянии а от нити. Направлен вектор перпендикулярно нити, если + - от нее, если  , то к нити.

7. Поток вектора напряженности через заданную поверхность. Теорема Гаусса в интегральной форме.

Поток вектора напряженности через заданную поверхность.

Так как электростатическое поле является векторным полем, которое можно изображать графически с помощью электрических силовых линий, к нему применимо понятие поток.

Рассмотрим в однородном поле элементарную площадку ds, ориентированную под углом α к . где  - угол между нормалью, и вектором

Поток вектора напряженности сквозь элементарную площадку ds зависит от величины вектора напряженности и от ориентации этой площадки по отношению к линиям напряженности.

Для произвольной поверхности и произвольного поля поток вектора через эту поверхность будет равен 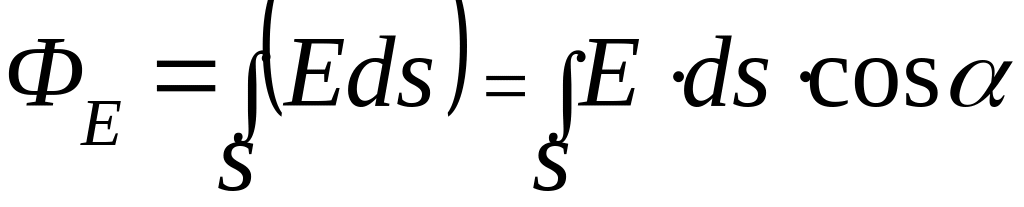где Еcos  = Еn – проекция вектора напряженности на направление нормали.

Если поле однородное, то ФЕ = Е∙Scos α

Как видно из формул ФЕ > 0, если α – угол острый и ФЕ < 0, если α – угол тупой

Теорема Остроградского – Гаусса

Рассмотрим сферическую замкнутую поверхность S, в центре которой находится точечный заряд q

Линии напряженности поля, создаваемого зарядом q направлены от заряда радиально

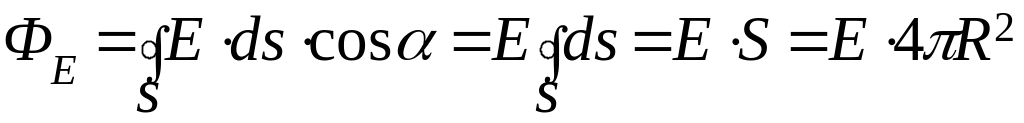
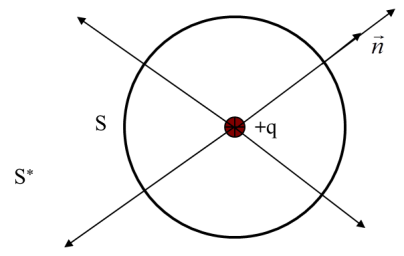
Изменим замкнутую сферическую поверхность S на произвольную замкнутую поверхность S*.

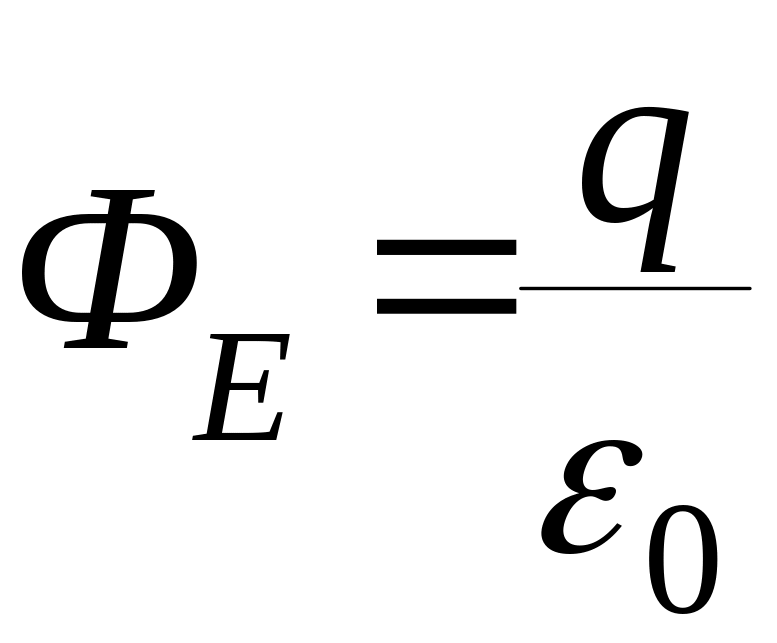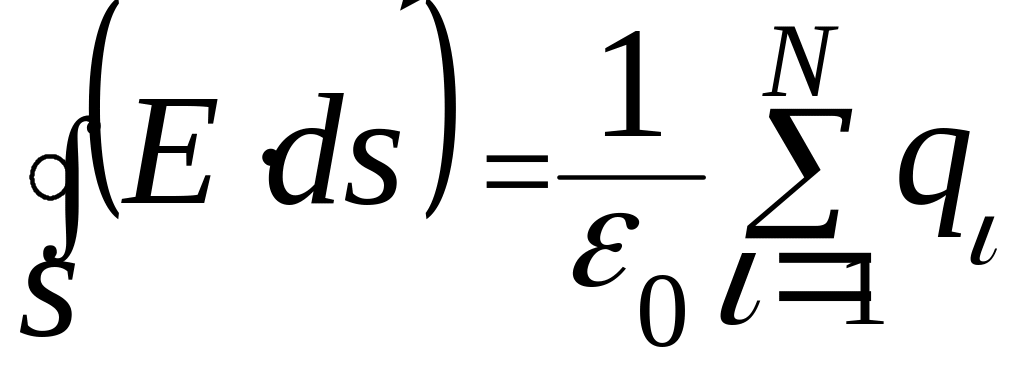Если поле создается не одним точечным зарядом, а системой точечных зарядов, то по принципу суперпозиции математическим выражением теоремы Гаусса в системе СИ. поток вектора напряженности через замкнутую поверхность равен алгебраической сумме зарядов, которые она охватывает

Если заряд распределен в объеме замкнутой поверхности непрерывно, то

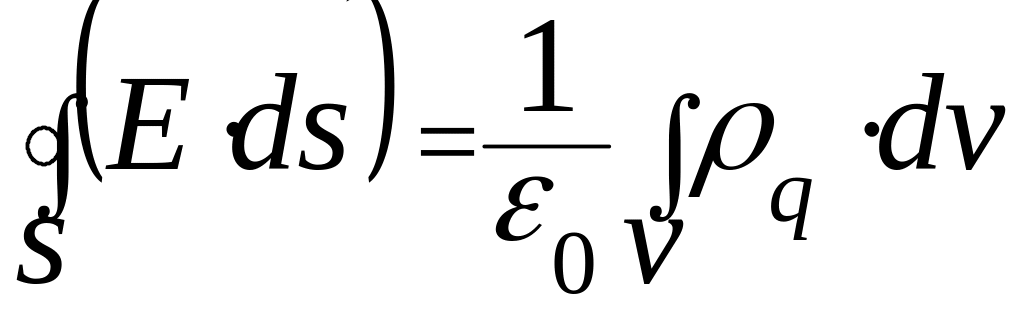
это интегральная форма записи теоремы Гаусса.