1. Электрический заряд и его свойства.

Электромагнитные явления обусловлены способностью некоторых частиц – фермионов

(электрон, протон ) взаимодействовать путём обмена фотонами.

Эта способность названа электрическим зарядом

В настоящее время твердо установлено, что электрические заряды существуют в виде

элементарных заряженных частиц – электронов и протонов

Условно считают, что электрон является носителем элементарного отрицательного заряда,

а протон – элементарного положительного заряда.

кл

Электрон происходит

от греческого «янтарь»

То, что янтарь, натертый о шерсть, приобретает способность притягивать легкие предметы, известно было в глубокой древности.

Несмотря на обилие веществ в природе, существуют только два вида электрических зарядов – отрицательные и положительные.

Свойства электрического заряда

1. Дискретность (квантованность) электрического заряда.

Любой заряд в целое число раз больше элементарного заряда (заряда электрона),

то есть заряд может принимать только строго определенные значения, а не любые.

Q = n |e|, где n = 1, 2, 3,…..

Такие величины, которые могут изменяться только на определенные порции (кванты), называют квантованными или дискретными.

2. Инвариантность заряда.

Электрический заряд не зависит от того, движется он или покоится, то есть он инвариантен по отношению к системе отсчета.

Телу можно сообщить заряд, перенося на него электроны или удаляя с него электроны. Тело, имеющее избыток электронов, заряжено отрицательно, тело, имеющее недостаток электронов – заряжено положительно.

3. Закон сохранения заряда.

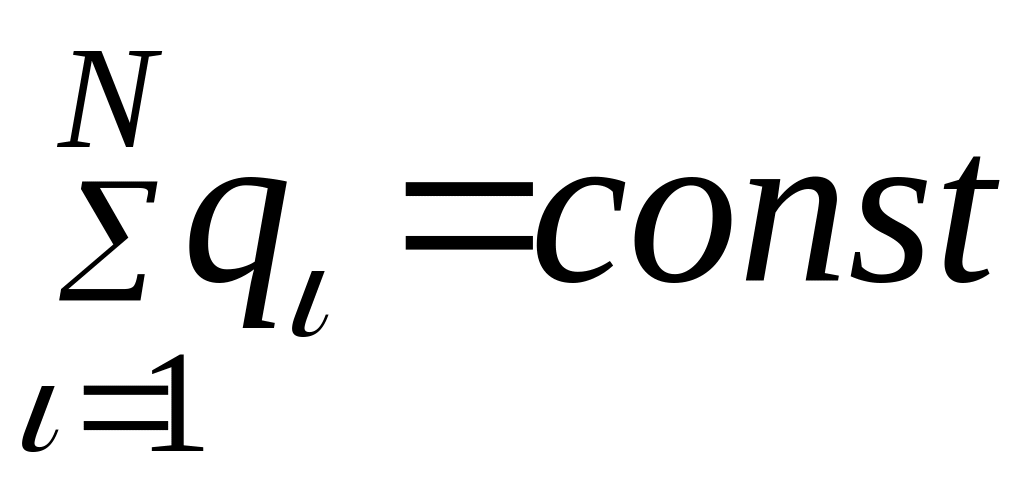
В замкнутой системе суммарный электрический заряд (алгебраическая сумма зарядов) остается постоянным.

За единицу эл. заряда в системе СИ принят 1Кл (Кулон) – заряд, проходящий за 1с. через сечение проводника, в котором имеется не изменяющийся ток силой в 1А..

Электростатика рассматривает статические, то есть неподвижные заряды и статические, не меняющиеся со временем электрические поля.

Под точечным зарядом понимают заряженное тело, размеры которого малы по сравнению с расстоянием до других зарядов.

2. Закон Кулона в векторной форме. Принцип суперпозиции кулоновских сил.

Закон Кулона

Сила взаимодействия 2х неподвижных точечных зарядов пропорциональна произведению величин зарядов и обратно пропорциональна квадрату расстояния между ними.

где k – коэффициент пропорциональности, зависящий от выбора системы единиц

(в СИ k = 1/40, где 0 = 8,85∙10¯¹² ф/м электрическая постоянная);  единичный вектор, направленный по прямой, соединяющей заряды q1 и q2.

Этот закон Кулон установил опытным путём, используя крутильные весы.

На тонкой кварцевой нити был подвешен горизонтальный стержень с маленьким заряженным шариком на конце. Второй заряженный шарик подносился к первому на некоторое расстояние в той же горизонтальной плоскости. В результате электростатических сил притяжения или отталкивания ( в зависимости от знаков обоих зарядов) упругая нить закручивалась на некоторый угол, тем больший, чем больше была сила взаимодействия между зарядами.

Величина кулоновской силы:

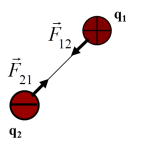
_{В случае одноименных зарядов она соответствует отталкиванию, в случае разноименных – притяжению.}

Принцип суперпозиции кулоновских сил.

Опыт показывает, что сила взаимодействия двух данных зарядов не изменится, если вблизи них поместить еще какие – либо заряды.

Пусть имеется точечный заряд qA и кроме того N точечных зарядов: q1, q2, q3,……qN

Результирующая сила , с которой действуют все N зарядов на заряд qА определяется формулой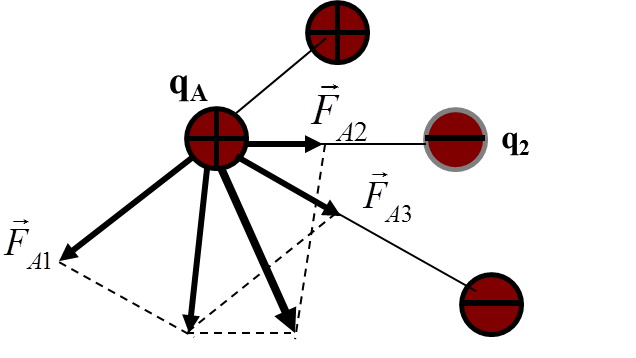

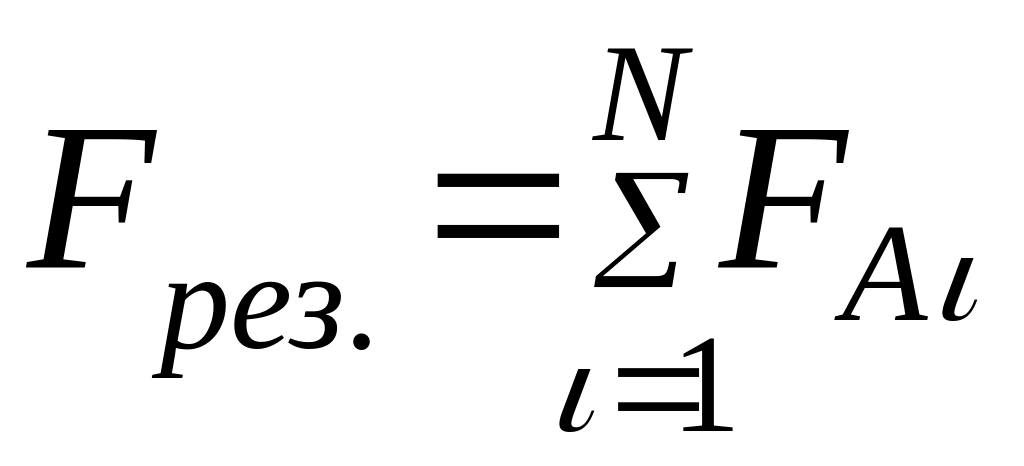
где - сила, с которой действует на qA i-ый заряд в отсутствии остальных.

Формула представляет собой математическое выражение принципа суперпозиции кулоновских сил.

3.Применение закона Кулона и принципа суперпозиции для расчеты силы взаимодействия между равномерно заряженным стержнем и точечным зарядом. Закон Кулона и принцип суперпозиции позволяют вычислить силу взаимодействия между заряженными телами, между заряженным телом и точечным зарядом.

Для этого надо:

1.Тела разбить на элементарные участки с зарядом dq, которые можно считать точечными;

2.Найти силу взаимодействия между зарядами dq попарно по закону Кулона;

3.По принципу суперпозиции найти результирующую силу

Определить силу взаимодействия равномерно заряженного тонкого стержня и точечного положительного заряда q.

Длина стержня – L, линейная плотность заряда - +. Заряд находится на продолжении оси стержня на расстоянии а от его конца.

Порядок решения

1. Выбираем систему координат (ось х пусть совпадает с длиной стержня, начало отсчета – с концом стержня).

2. 2. Выделяем на стержне элементарный участок dx  dq на расстоянии х от начала координат.

Учитывая, что заряд, распределенный по длине, характеризуется линейной плотностью  =q/L, найдем, что dq = dx

3. По закону Кулона находим направление и величину силы 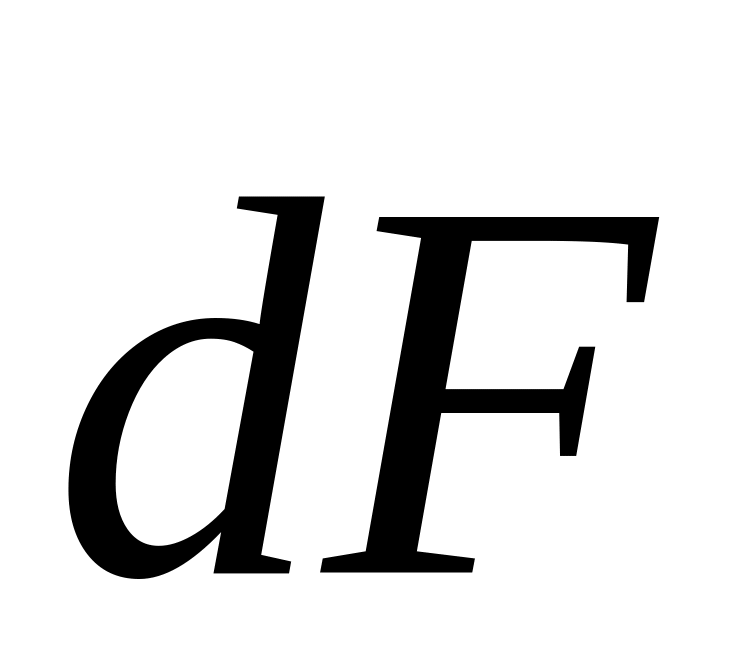- силы взаимодействия между dq и q.

4. По принципу суперпозиции находим
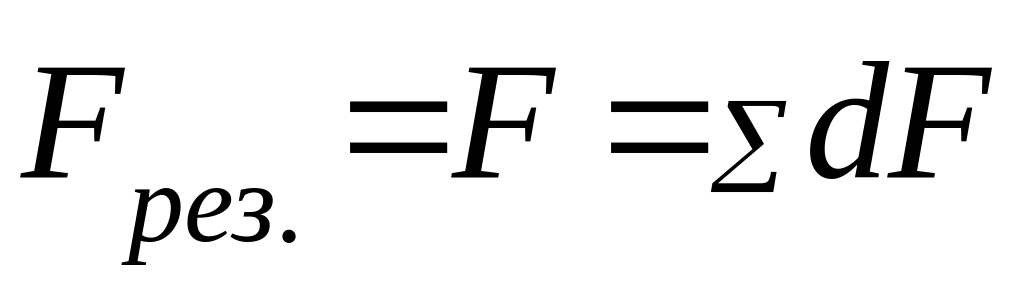