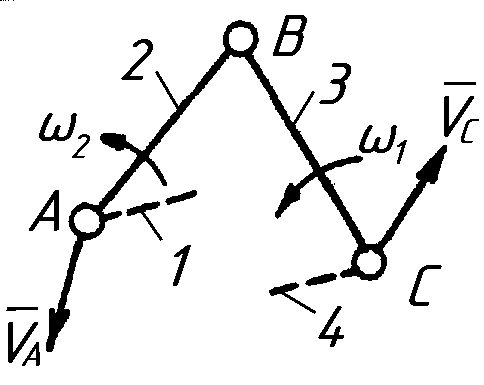
2.3. Планы скоростей рычажного механизма

Планы скоростей механизма строят на основе аналитических зависимостей векторных уравнений, которые записывают для каждой структурной группы в порядке их присоединения начальному звену. В табл. 2.1 показаны векторные уравнения и планы скоростей для структурных групп 2-го класса 1-5 видов.

Пример выполнения кинематического анализа методом планов

Для определения скоростей используем графоаналитический метод, т.е. аналитически определим скорость точки В:

м/с.

Табл. 2.1

Вид	Расчетные схема структурных групп	Векторные уравнения	План скоростей
1
2
3
4
5

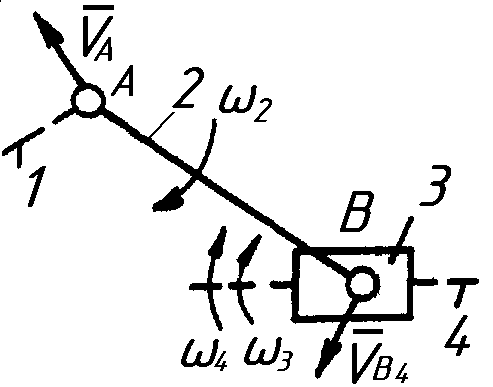
Рассмотрим структурную группу 2-3, в которой и поскольку звенья 1-2 и 2-3 соединены шарнирно:

где = 4,2 м/с; = 0, т.к. точка расположены на неподвижном звене;  звену , вращательная скорость т. вокруг ; V_С3С0  звену 0, поступательная скорость т. по звену 0.

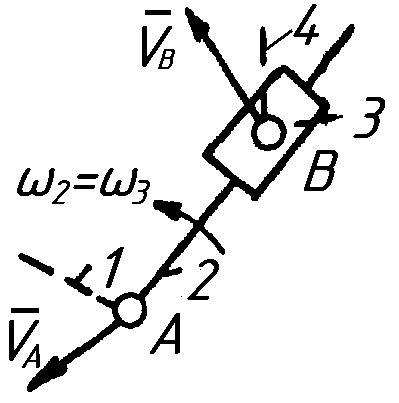
Решение векторных уравнений осуществим графически, т.е. построим план скоростей (рис. 2.4. Приложение Б). Для этого выбираем масштабный коэффициент скоростей:

= 0,05 м ∙ c^-1 /мм,

где - отрезок, выражающий скорость т. , принимаем равным = 84 мм.

Решим графически систему векторных уравнений для т. , т.е. из точки проводим линию  , а из полюса - линию  звену 0.

На пересечении линий получим точку и соответственно скорости:

= 86∙ 0,05 = 4,3 м/с,

= 42 ∙ 0.05 = 2,1 м/с.

Определим угловую скорость шатуна

= = 17,5 рад/с.

Угловая скорость направлена в сторону относительной скорости.

Определим скорость центра тяжести звена S₂ методом подобия. Точка S₂ принадлежит звену ВС и делит звено в заданном соотношении . Относительные скорости при этом будут пропорциональны отношению

откуда

= 42 ∙ = 28 мм.

Отложим отрезок bs₂ на линии bс и точку S₂ соединим с полюсом.

Скорость центра тяжести S₂ определяется выражением

= = 83∙ 0,05 = 4,15 м/с.

Аналогично определяется скорость т. S₁

;

= 84∙ = 36 мм;

∙ m_v = 36 ∙ 0,05 = 1,8 м/с.

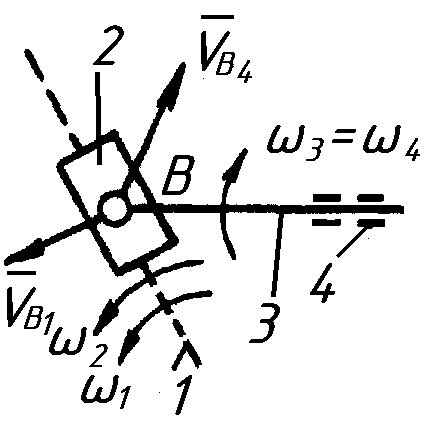
Планы ускорений как и планы скоростей, строятся на основе векторных уравнений, составленных для каждой структурной группы (табл.2.2). Структурные группы следует рассматривать в соответствии с порядком их присоединения к основному механизму.

Табл. 2.2.

Вид	Расчетные схема структурных групп	Векторные уравнение	План ускорений
1
2
3
4
5

Для определения ускорения точек строим план ускорений, который строится аналогично плану скоростей. Ускорения т. В₁:

; ,

где = 60² ∙ 0,07 =252 м/с²,

= 80 ∙ 0,07 = 5,6 м/с² .

Выберем масштабный коэффициент мс^-2/мм и строим план ускорений (рис. 2.5. Приложение Б)

Отрезок плана ускорений, выражающий точку В:

= = 100,8 мм,

= = 2,24 мм.

Определим ускорение т. С путем графического решения системы векторных уравнений:

где ;

- известно и определяется вектором ;

=101 ∙ 2,5 = 252,5 м/с²;

17,5² ∙ 0,12 =36,75 м/с² - нормальное ускорение во вращательном движении т. С вокруг В;

- кариолисово ускорение равно 0, при неподвижной направляющей;

- тангенциальное ускорение во вращении т. С вокруг В, направлено  СВ;

- относительное ускорение поступательного движения звена 3 по звену 0.

На пересечении этих направлений получим ускорение точки С_2,3:

30 × 2,5 = 75 м/с²;

90 ×2.5 = 225 м/c²;

30 × 2,5 = 75 м/с².

Отрезок нормального ускорения

мм

откладывается от точки C к В  звену ВС.

Определим угловое ускорение звена 2

= = 1875 рад/с².

Направление углового ускорения определяется тангенциальной составляющей линейного ускорения.

Используя метод подобия определим ускорение центра тяжести звена S₁

; = 43,2 мм;

43,2 ∙ 2,5= 108 м/с².

Используя метод подобия определим ускорение центра тяжести звена 2

, откуда = 91 ∙ = 60,67 мм.

Отложим отрезок на линии плана ускорений и соединим с полюсом.

Тогда ускорение т. S₂ определяется зависимостью

= 60,67 ∙ 2,5= 151,67 м/с².