8.Три критерия оценки структуры баланса и платежеспособности предприятия.
Платежеспособность и финансовая устойчивость – это способность предприятия расплачиваться своевременно по своим обязательствам.
=
=
=
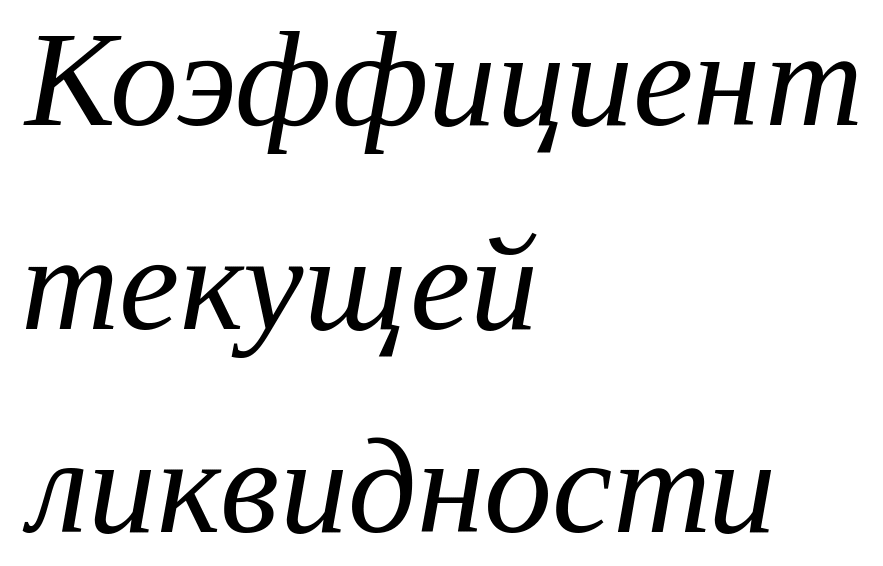Все три условия должны соблюдаться одновременно.
9.Сущность факторного анализа на примере использования интегрального метода и метода цепных подстановок.
Факторный анализ – установление количественных зависимостей базовых результатов от фактообразующих показателей (параметров).
Индексный метод (взвешанных конечных разностей, логарифмический).
Дифференциальное исчисление.
Интегральный метод.
Метод цепных подстановок.
Метод цепных подстановок: это один из способов разложения абсолютного отклонения результирующего показателя. Например, установлена функциональная зависимость результирующего показателя (Ф) от четырех факторов: а, в, с, д. Сравнивая фактическое значение с его плановым или базовым значением, получаем отклонение, которое связано с изменением значений четырех факторных признаков.
Схема использования метода цепных подстановок
Номер расчета |
Номер подстановки |
Взаимодействующие частные показатели |
Ф |
Факторы |
|
|||
а |
в |
с |
д |
|||||
1 |
- |
Ап |
Вп |
Сп |
Дп |
Фп |
- |
- |
2 |
1 |
Аф |
Вп |
Сп |
Дп |
Ф1 |
А |
Ф1-Фп |
3 |
2 |
Аф |
Вф |
Сп |
Дп |
Ф2 |
В |
Ф2-Ф1 |
4 |
3 |
Аф |
Вф |
Сф |
Дп |
Ф3 |
С |
Ф3-Ф2 |
5 |
4 |
Аф |
Вф |
Сф |
Дф |
Фф |
Д |
Фф-Ф3 |
Таким образом, сущность метода заключается в последовательной замене каждого факторного показателя с планового значения на его фактическое значение, при этом все остальные рассматриваются как неизменные.
Число подстановок зависит от количества факторов, составляющих модель расчета показателя. Модель расчета результирующего показателя – это всякий раз базовая формула, в которой закреплены установленные взаимосвязи между факторными и результирующими показателями. Расчеты начинаются с исходной базы, когда все факторы равны плановому или базисному значению. Степень влияния каждого фактора устанавливается путем последовательного вычитания: из второго расчета значение первого, из третьего – второе и т. д.
Метод цепных подстановок используется для анализа отклонений значений результирующих показателей, которые представляют собой жестко детерминированные модели.
Применение приема цепных подстановок требует строгой последовательности определения влияния факторов.
Произвольное изменение последовательности подстановки меняет количественную весомость того или иного показателя.
Интегральный метод: если трудно определить характер показателя, с тем чтобы правильно установить последовательность подстановок, можно воспользоваться интегральным методом. При использовании данного метода участники формулы признаются равнозначными. Интегральный метод позволяет полностью разложить результативный показатель по факторам и носит универсальный характер. То есть он применим к мультипликативным, кратным и смешанным моделям. Операция вычисления интеграла решается с помощью ЭВМ либо специальных таблиц. Изменение результирующего показателя измеряется на очень малых отрезках изменения факторов и производится суммирование приращения результата, определяемого как частные производные, умноженные на приращения факторов на бесконечно малых промежутках.
Например, модель вида y = a * b может быть проанализирована с использованием следующих формул:
∆y (a) = bo * ∆a + ½ ∆a * ∆b
∆y (b) = ao * ∆b + ½ ∆a * ∆b
Модель вида y = a * b * c:
∆y (a) = ½ ∆a (b0c1 + b1c0) + 1/3 ∆a ∆b ∆c
∆y (b) = ½ ∆b (a0c1 + a1c0) + 1/3 ∆a ∆b ∆c
∆y (c) = ½ ∆c (a0b1 + a1b0) + 1/3 ∆a ∆b ∆c
Модель вида y = a / b:
∆y (a) = ∆a / ∆b * Ln│b1 / b0│
∆y (b) = ∆y – ∆y (a)
Модель вида у = a / (b + c):
∆y (a) = ∆a/(∆b + ∆c) * Ln│(b1 + c1)/(b0 + c0)│
∆y (b) = (∆y – ∆y(a)) / (∆b + ∆c) * ∆b
∆y (c) = (∆y – ∆y(a)) / (∆b + ∆c) * ∆c