25. Теорема о втором замечательном пределе.
Доказательство.
Доказательство второго замечательного предела для случая последовательности (т.е. для
Натуральных значений x)
Докажем вначале теорему для случая последовательности 
По формуле бинома Ньютона: 
Полагая 
, получим:
(1)
Из данного равенства (1) следует, что с увеличением n число положительных слагаемых в
правой части
увеличивается. Кроме того, при увеличении n число 
убывет, поэтому величины 
возрастают. Поэтому последовательность 
— возрастающая, при этом
(2).
Покажем, что она ограничена. Заменим каждую скобку в правой части равенства на единицу,
правая часть увеличится, получим неравенство
Усилим полученное неравенство, заменим 3,4,5,…, стоящие в знаменателях дробей, числом 2:
.
Сумму в скобке найдем по формуле суммы членов геометрической прогрессии:
.
Поэтому 
(3).
Итак, последовательность ограничена сверху, при этом 
выполняются неравенства (2) и (3): 
.
Следовательно, на основании теоремы Вейерштрасса (критерий сходимости последовательности) последовательность 
монотонно возрастает и ограниченна, значит имеет предел, обозначаемый буквой e. Т.е. 
Зная, что второй замечательный предел верен для натуральных значений x, докажем второй
замечательный предел для вещественных x, т.е. докажем, что 
Рассмотрим два
случая:
1. Пусть 
каждое значение x заключено между двумя положительными целыми числами: 
, где n =
[x] - это целая часть x.
Отсюда следует: 
, поэтому
.
Если 
, то 
. Поэтому, согласно пределу 
, имеем:
.
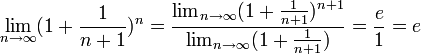
По признаку (о пределе промежуточной функции) существования пределов 
.
2. Пусть 
. Сделаем подстановку − x = t, тогда
.
Из двух этих случаев вытекает, что 
для любого x.
26. Теорема о замене переменной в пределах. Следствие из теоремы о втором замечательном пределе.
Если существуют
и 
причем
для всех х из некоторой проколотой
окрестности точки 
выполняется
условие 
,
то в точке 
существует предел сложной функции 
и
справедливо равенство
|
Проводим доказательство, используя определение предела функции по Гейне
|
Следствия:
Доказательство следствия
27. Следствия 2-4 из теоремы о втором замечательном пределе.
Замечательный логарифмический предел
Доказательство предела
Замечательный показательный предел
Следствия
для 
, 
Доказательство предела
Доказательство следствия
Замечательный степенной предел
Доказательство предела
28. Теорема о первом замечательном пределе.
Доказательство
Рассмотрим односторонние пределы 
и 
и докажем, что они равны 1.
Пусть 
. Отложим этот угол на единичной окружности (R = 1).
Точка K — точка пересечения луча с окружностью, а точка L — с касательной к единичной окружности в точке(1;0). Точка H — проекция точки K на ось OX.
Очевидно, что:
(1)
(где SsectOKA — площадь сектора OKA)
(из 
: | LA |
= tgx)
Подставляя в (1), получим:
Так как при 
:
Умножаем на sinx:
Перейдём к пределу:
Найдём левый односторонний предел:
Правый и левый односторонний пределы существуют и равны 1, а значит и сам предел равен 1.