3. Выявление места и причины затруднения.
Цель:
1) выявить и зафиксировать место и причину затруднения.
Организация учебного процесса на этапе 3:
Какой следующий шаг вы должны сделать? (Разобраться, в чем затруднение.)
Какое задание вы выполняли? (Мы должны были найти разность чисел 14 и 7.)
Чем это задание отличается от предыдущих? (Мы должны были найти разность за короткое время.)
Чем пытались воспользоваться? (Помощниками – таблицей сложения и числовым отрезком.)
Что же не получилось? (Их использование требует времени.)
Почему возникло затруднение? (Нет удобного способа вычитания с переходом через разряд.)
4. Построение проекта выхода из затруднения.
Цель:
построить проект выхода из затруднения.
Организация учебного процесса на этапе 4:
Какова же цель вашей дальнейшей деятельности? (Открыть способ, с помощью которого мы могли быстро вычитать числа с переходом через разряд.)
Сформулируйте тему урока. (Вычитание с переходом через разряд.)
Учитель открывает тему урока.
Вспомните, как вы открывали алгоритм сложения с переходом через разряд? (Нам помогали графические модели.)
Как вы будете действовать? (Мы запишем числа с помощью графических моделей, выполним действие, сделаем вывод.)
Учитель может план зафиксировать на доске.
5. Реализация построенного проекта.
Цель:
1) организовать коммутативное взаимодействие с целью реализации построенного проекта, направленного на приобретение недостающих знаний;
2) организовать фиксацию построенного способа действия в речи и знаково (с помощью эталона);
3) организовать уточнение общего характера нового знания.
Организация учебного процесса на этапе 5:
Выполните план в группах.
Группы работают на индивидуальных планшетках.
По окончанию работы, представители от каждой группы вывешивают на доску свой результат (графическая модель равенства).
Итак, какой результат вы получили?
Представитель от одной из групп комментирует свой ход работы:
Мы записали каждое число в виде графической модели. Поняли, что удобно вычесть сначала 4 единицы, чтобы «дойти» до десятка, а потом вычесть оставшиеся единицы из вычитаемого. Получили ответ 7.
Если учащиеся не смогли в группах выделить принципиальный шаг – вычитание из уменьшаемого единиц, - учитель организует подводящий диалог. В итоге у групп на планшетках должны получиться запись:
В случае возникновения сложностей у учащихся с реализацией плана, учитель организует подводящий диалог:
Какой первый шаг вы должны выполнить? (Заменить числа графическими моделями.)
Как обозначим числа 14? 7? (Треугольником с четырьмя точками и семью точками.)
Учитель изображает на доске выражение с помощью графических моделей.
Из скольких десятков и единиц состоит уменьшаемое? (Из одного десятка и четырех единиц.)
Сколько единиц удобно сразу взять из уменьшаемого? (4 единицы.)
Покажем это на нашей модели.
Один из учеников с помощью учителя обводит красным мелом 4 единицы в вычитаемом.
Сколько единиц осталось вычесть? (3 единицы.)
Почему? (7 это 4 и 3.)
Откуда вычтем оставшиеся единицы? (Из десятка, в десятке – 10 единиц.)
Покажите это на модели.
Один из учеников дополняет запись на доске.
Итак, в начале путешествия через разряд в путь отправятся 4 единички, а затем еще 3. Покажем их движение стрелочками.
Один из учеников с помощью учеников проводит красным мелом стрелочки от обведенных единиц к вычитаемому.
Какой получится ответ? (7 единиц.)
Учитель дополняет модель разностью.
Сестрички-единички удивляются тому, как вам удалось без помощи таблицы найти разность. Помогите им восстановить рассуждений. Что вы делали в самом начале? (Определяли, сколько единиц в уменьшаемом.)
Учитель помещает на доске первый шаг алгоритма Д-9.
Что делали потом? (Разбивали 14 на 4 и 3.)
Учитель размещает на доске второй шаг алгоритма Д-9.
А потом? (Из 14 вычли сначала 4, а потом 3.)
Учитель дополняет алгоритм.
Покажите порядок выполнения действий стрелочками.
Но неужели при выполнении вычитания такого вида вам всякий раз необходимо будет переводить числовое выражение в графическую модель? Вспомните, как это делали при сложении чисел такого вида. (С помощью «усиков».)
Учитель на доске для образца дополняет запись, остальные учащиеся делают запись на планшетках или в рабочих тетрадях:
Как узнать, верно ли решен пример? (Можно проверить по таблице сложения или числовому отрезку.)
Как еще? (Выполнить обратное действие – сложение.)
Выполните обратное действие.
Один из учеников выполняет действие на доске, остальные учащиеся на планшетках.
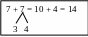
Проверьте открытие.
Учитель раздает учащимся эталоны Р-2.
Сделайте вывод. (Мы все правильно окрыли.)
Каким же помощником вы можете воспользоваться при вычитании чисел с переходом через разряд? (Новым эталоном.)
Что он вам позволяет? (Решать быстро примеры на вычитание чисел с переходом через разряд.)
Какой следующий шаг мы должны сделать? (Потренироваться в использовании нового способа.)