- •I. Расчет рамы на свободные колебания
- •1 . Вводная информация
- •3. Формирование исходных матриц уравнения (1)
- •4. Алгоритм решения матричного квадратного уравнения (мку)
- •5 . Пример нахождения u и V для заданных матриц m, c, k
- •6. Определение параметров собственных колебаний рамы
- •6.1. Общие сведения о характеристиках собственных колебаний
- •6.2. Определение коэффициентов демпфирования, частот и форм собственных колебаний рамы
- •6.3. Анализ результатов собственных колебаний рамы
- •7. Функции MatLab
- •I I. Расчет рамы на вынужденные колебания
- •1 . Расчет рамы на действие вибрационной нагрузки (рис. 5)
6.2. Определение коэффициентов демпфирования, частот и форм собственных колебаний рамы
Спектральное разложение S в базисе из собственных векторов (11):
S
= PP–1
=
 ,
,
г де
де
=
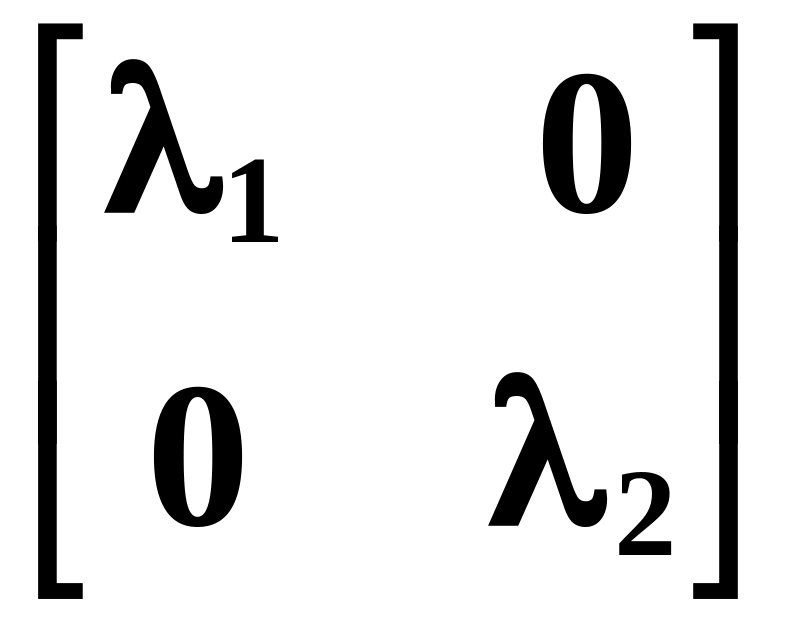 =
=
 =
=
=

=
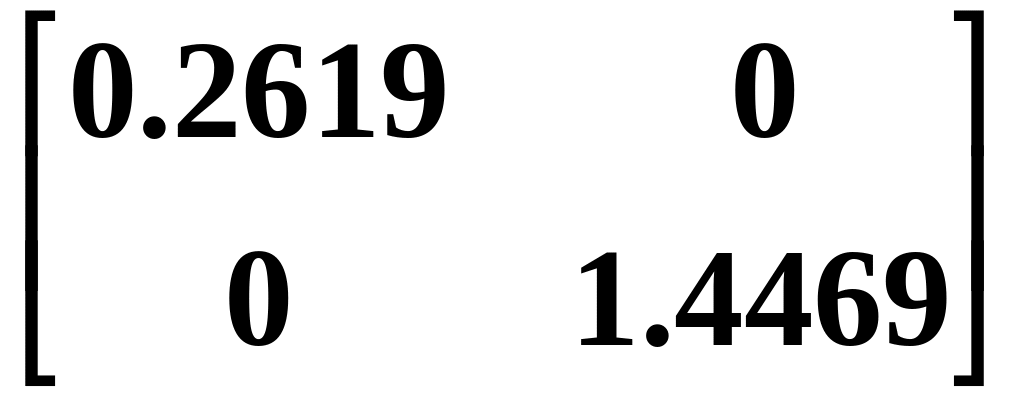 ,
=
,
=
 .
.

P
=
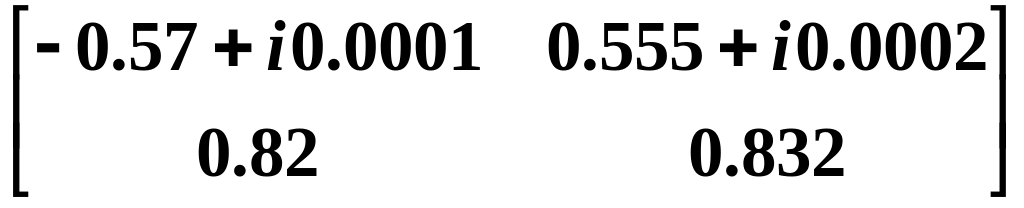 ,
P1
=
,
P1
=
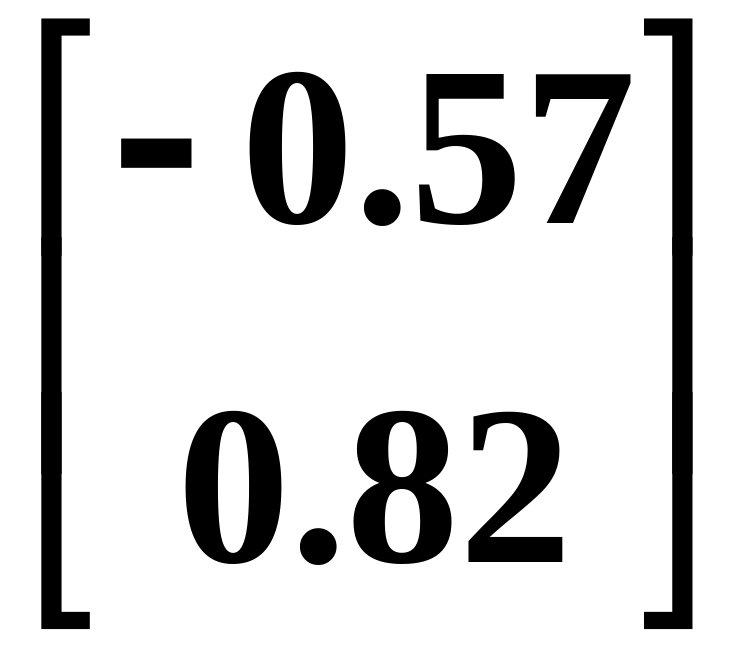 ,
P2
=
,
P2
=
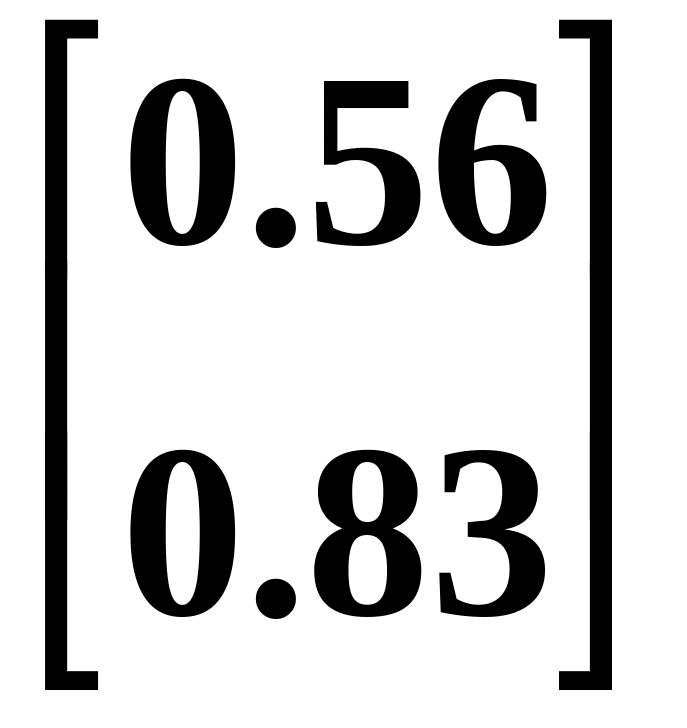
6.3. Анализ результатов собственных колебаний рамы
Ф
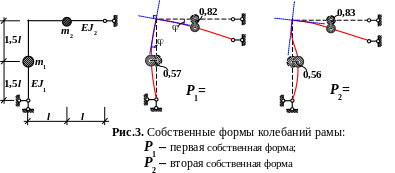 ормы
собственных колебаний
ормы
собственных колебаний

Параметры собственных колебаний: частоты и коэффициенты демпфирования
7. Функции MatLab
i nv(A)
– операция
обращения матрицы A
(эквивалентно действию A–1);
nv(A)
– операция
обращения матрицы A
(эквивалентно действию A–1);
eig (A) – выполняет операцию разложения матрицы A в базисе из собственных векторов: A = PP–1, где P – матрица собственных векторов, = diag (1, … , n) – матрица собственных значений матрицы A.
По этой команде выводятся только собственные значения k в виде вектора: [1, 2, … , n]T; по команде [P ] = eig (A) на печать выводится матрица P и диагональная матрица собственных значений;
sqrtm (A) – извлечение корня квадратного из A. Выполняется с помощью разложения в базисе из собственных векторов матрицы A = PP–1, как функция от матрицы: f(A) = P f()P–1 (P и – матрицы собственных векторов и значений матрицы A);
expm (A) – матричная экспонента (операция эквивалентна действию eA); выполняется с учетом спектрального разложения eA = PeP–1, где A = PP–1. В частности, для функции Ф(t) = eSt expm(S*t);
eye (n) – операция формирования единичной матрицы E n-го порядка;
A2 – возведение матрицы в квадрат: A^2 (можно, и даже лучше, квадрат записать через произведение: A2 = A*A); в общем случае: Am A^m;
A’ – операция транспонирования матрицы A:
если A – действительная: A Mn(R), то эта операция эквивалентна AТ;
если
A
– комплексная:
A
Mn(С),
то эта операция
эквивалентна сопряжению
![]() ;
;
A.’ – операция транспонирования комплексной матрицы A Mn(С): эквивалентна действию AТ (добавление точки снимает операцию сопряжения).
Практика 3
I I. Расчет рамы на вынужденные колебания

Уравнение движения вынужденных колебаний рамы
M (t) + C (t) + KY(t) = F(t) (14)
1 . Расчет рамы на действие вибрационной нагрузки (рис. 5)
F(t) = sin tP0,
P0
=
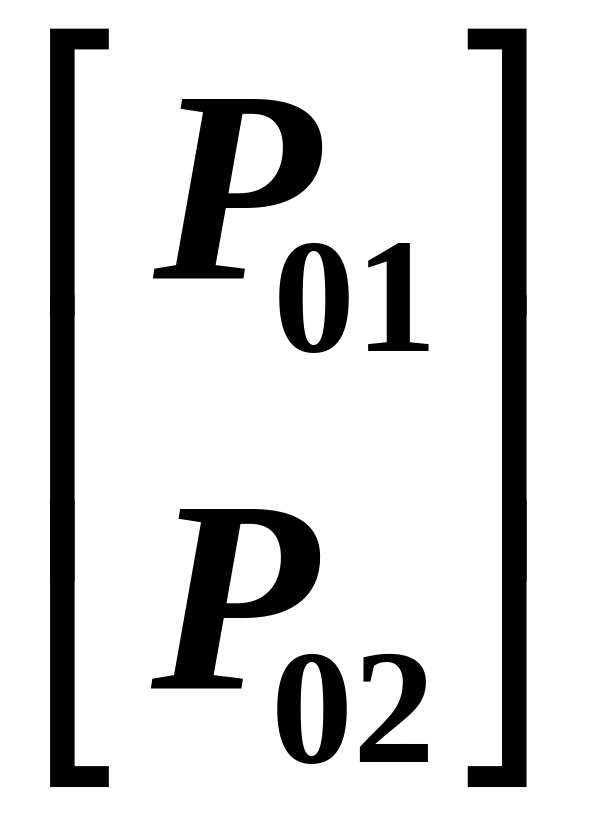 ,
=
,
=

Для расчета принять:
P01 = 20 кН; P02 = 0;
1 = 2 = 0,8 1 с-1;
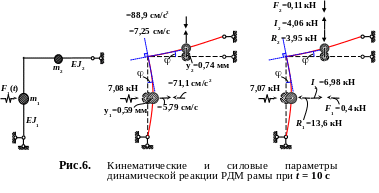
Определить из ур.(40), (42) все параметры динамич. реакции рамы при t = 10 c: перемещ., скорости, ускорения, восстанавл., диссипативные и инерционные силы.
Решение динамической задачи
Запись разрешающих уравнений (40), (42) (векторы перемещ. и скоростей):
 Y(t)
= 2Re [X(t)]P0,
Y(t)
= 2Re [X(t)]P0,
![]() (t)
= 2Re [SX(t)]P0,
(t)
= 2Re [SX(t)]P0,
X(t) = {S[Ф(t–t0)sin t0 – sin t ] +
[Ф(t–t0)cos t0 – cos t ]}[U(S2 + 2)]–1.
Для построения вектора ускорений дифференцируем выражение вектора скорости. Окончательно система уравнений при t0 = 0, = 0 имеет вид:
Y
(a)
![]() (t)
= 2Re
[S2X(t)]P0
+ M–1F(t),
(t)
= 2Re
[S2X(t)]P0
+ M–1F(t),
X (t) = { Ф(t) – Ssin t – cos t }[U(S2 + 2)]–1.
Система разрешающих уравнений (а) содержит векторы перемещений, скоростей и ускорений. Данные величины представляют кинематические параметры реакции системы.
Построение силовых параметров реакции системы.
В
 ектор
восстанавливающих сил: R(t)
= KY(t)
ектор
восстанавливающих сил: R(t)
= KY(t)
В
(б)![]() (t)
(t)
Вектор
инерционных сил: I(t)
= –M![]() (t)
(t)
Построение матрицы X(t) в (а).
Так как матрица скалярная, то ее можно представить в виде скаляра (числа)
= 0,8 1 = 0,842.4567 = 33.96536 c1 и тогда матрица X(t) запишется так:
X(t) = { Ф(t) – Ssin t – Ecos t }[U(S2 + E2)]–1.
Вычисляем в этом выражении вспомогательные функции при t = 10 c :
sin t = 0.3538; cos t = 0.9353; cos t = 31.769; отсюда получим:
X
(в)
Определяем матрицы, стоящие в фигурных скобках в (в):
0.3538*S = 0.3538* =
=
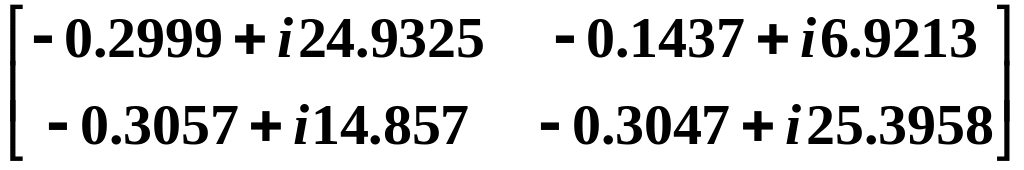 ,
,
Ф(10)
= e10S
=
 ,
,
33.96536*Ф(10)
=
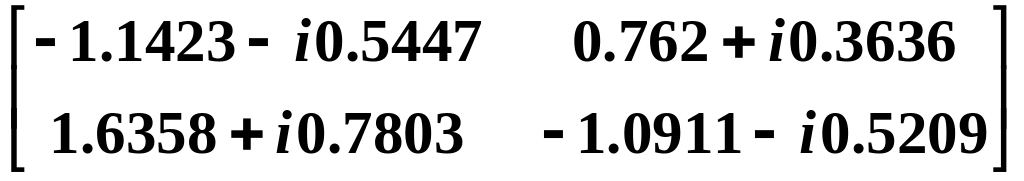 ,
,
31.769*E
= 31.769*![]() =
=
![]() .
.
Тогда фигурная скобка в выражении (в) матрицы X(10) равна:
{ 33.96536*Ф(10) – 0.3538*S – 31.769*E} =
=
(г)
Вычисление второй матрицы-сомножителя в (в): [U(S2 + 1153.646*E)]–1.
U
=
i
кНс
/ м =
i
 кНс
/ см.
кНс
/ см.
S2
=
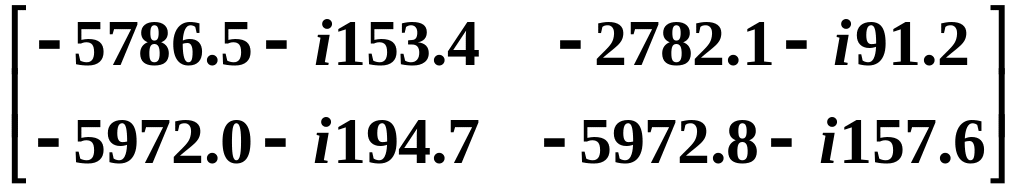
[U*(S2 + 1153.646*E)] =
=
i
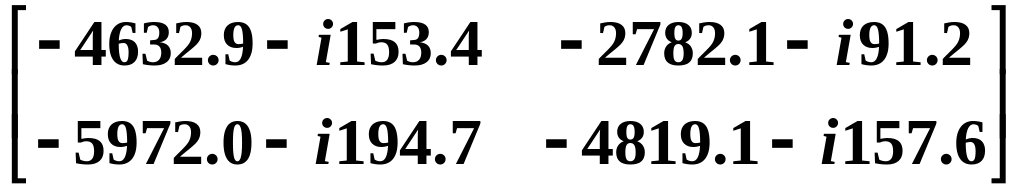 =
=
=
 .
.
[U(S2 + 1153.646*E)]–1 =
=
(д) 10-5
10-5
Окончательно матрица X(10) в (в) равна произведению (г)*(д):
X(10)
=
 *
*
*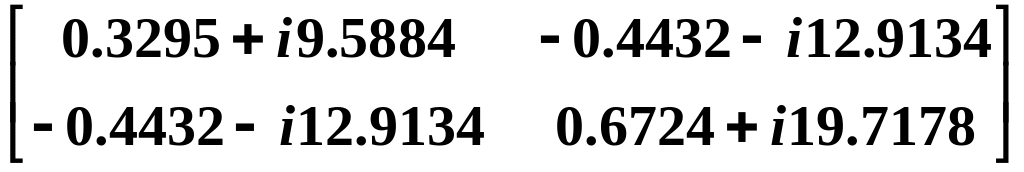 10-5
=
10-5
=
=
 10-2,
10-2,
Из уравнений (а) получаем соотношения:
Y
(е)
 (10)
= 2Re [X(10)]P0,
(10)
= 2Re [SX(10)]P0,
(10)
= 2Re [X(10)]P0,
(10)
= 2Re [SX(10)]P0,
(10) = 2Re [S2X(10)]P0 + M–1F(10),
в которых необходимо вычислить следующие
величины:
которых необходимо вычислить следующие
величины:
Re [X(10)] = Re 10-2 =
=
(ж) 10-2;
10-2;

SX(10)
=
 ,
,
R
(з) ;
;
S2X(10)
=
 ,
,
R
(и)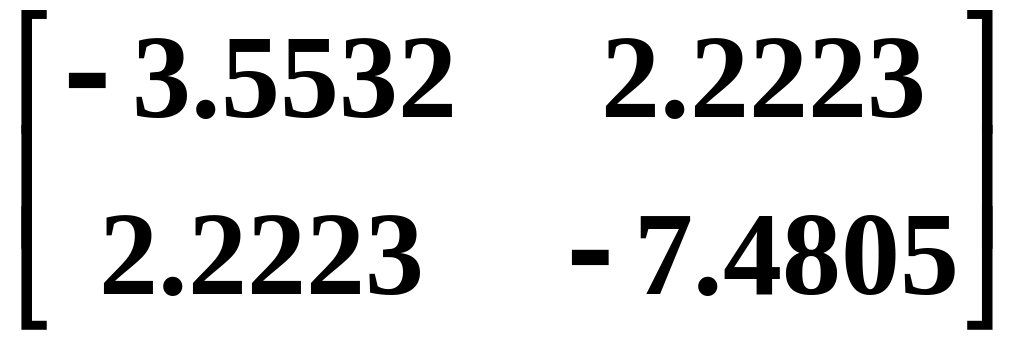

M–1
=

F(10)
= sin (10)P0
=
0.3538![]() =
=
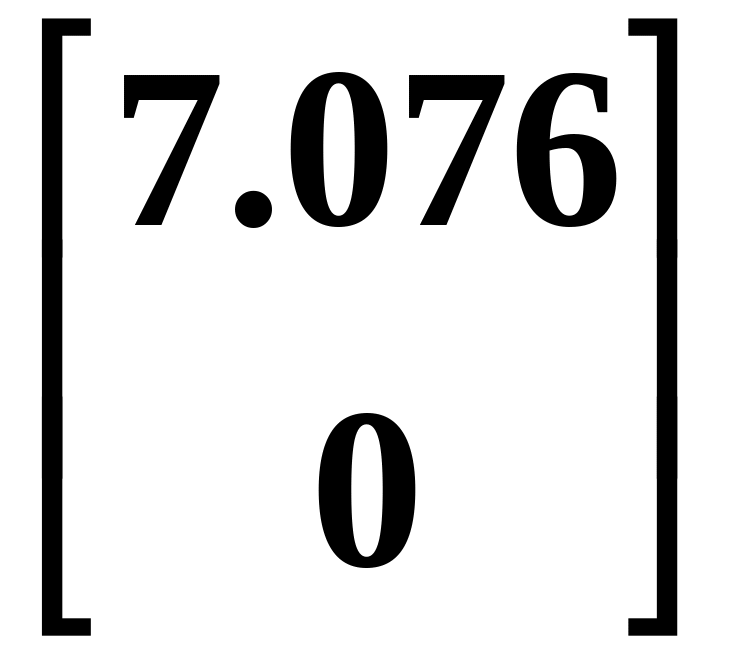 кН
кН
M
(к)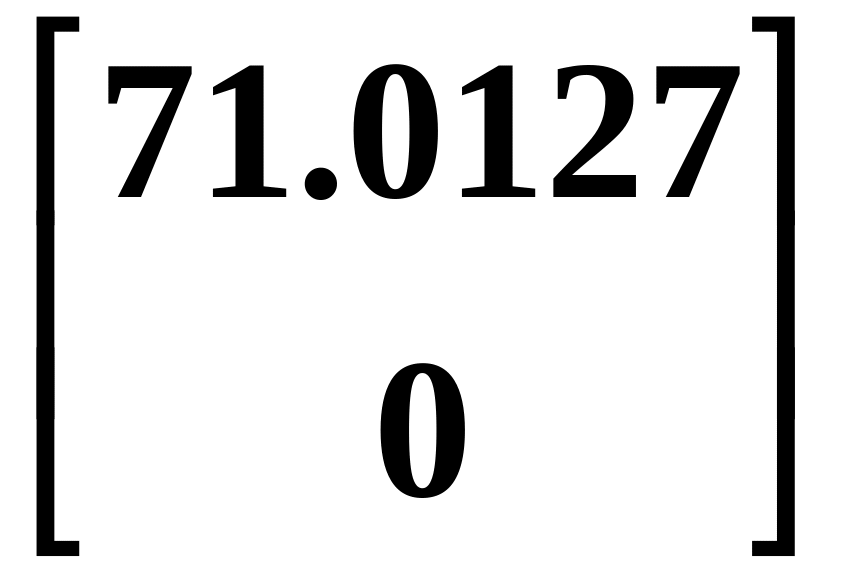 см/c2
см/c2
Кинематические параметры реакции рамы при t = 10 c
В ектор
перемещений с учетом (ж):
Y(10)
= 2Re
[X(10)]P0
=
ектор
перемещений с учетом (ж):
Y(10)
= 2Re
[X(10)]P0
=
=
2
10-2
=
 10-2
=
10-2
=
 см
см

Вектор скоростей с учетом (з): (10) = 2Re [SX(10)]P0 =
=
2
=
 см/c
см/c

Вектор ускорений с учетом (и) и (к):
(10) = 2Re [S2X(t)]P0 + M–1F(10) =
= 2 + =
=
 +
=
+
=
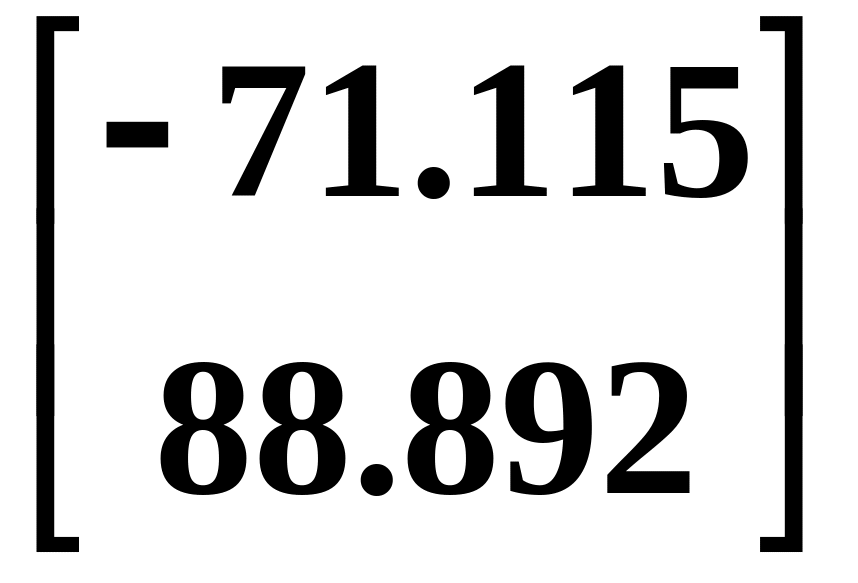 см/c2
см/c2
Силовые параметры реакции рамы при t = 10 c

Вектор восстанавливающих сил: R(10) = KY(10) =
=
 10-2
=
10-2
=
 кН
кН
Вектор диссипативных сил: F(10) = C (10) =
=
10-2
=
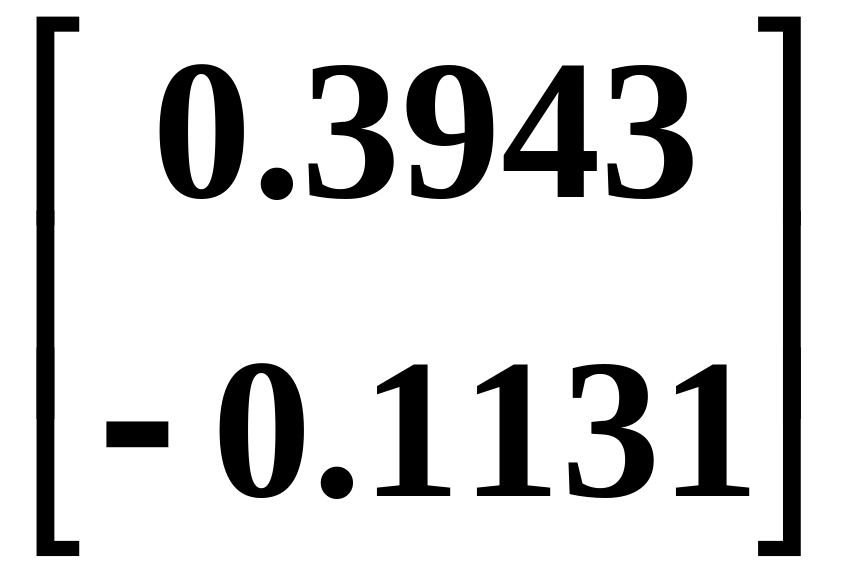 кН
кН
Вектор инерционных сил: I(10) = –M (10) =
=
–
10-2
=
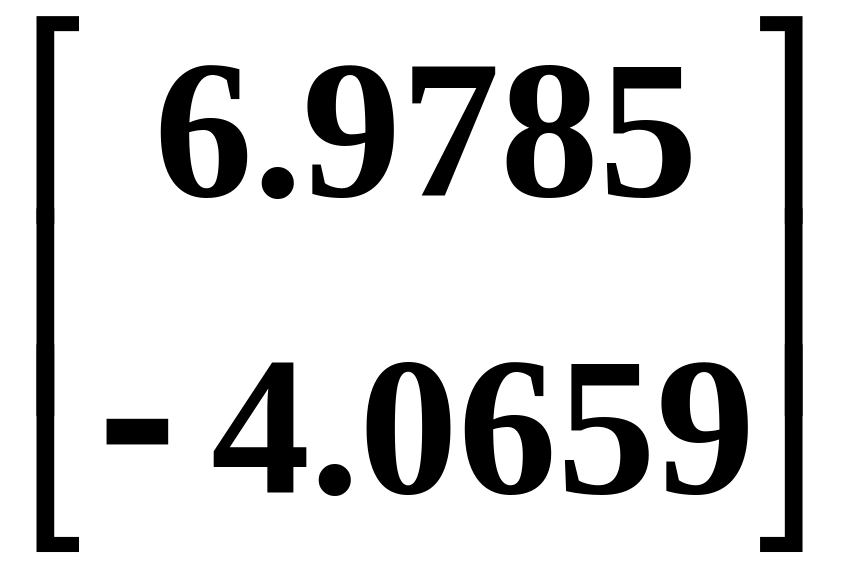 кН
кН