П рактика 1

Определение параметров собственных колебаний рамы

Д ано: l = 2 м

Модуль упругости: E = 2,110⁵ МПа

Массы: m₁ = 9,96 кНс² / м

m₂ = 4,64 кНс² / м

Моменты инерции двутавров:

J₁ = 64140 см4 (№ 40 К 2)

J₂ = 125930 см4 (№ 60 Б 2)

Жесткости стержней:

EJ₁ = 2,110⁸6414010^–8 = 134694 кНм²

EJ₂ = 2,110⁸12593010^–8 = 264453 кНм²

I. Расчет рамы на свободные колебания

1 . Вводная информация

Уравнение движения при свободных колебаниях рамы

M (t) + C (t) + KY(t) = 0. (1)

Построение матрицы жесткости K. Матрица жесткости K может быть получена из матрицы податливости L путем ее обращения: K = L^–1.

K

r_ik – реакция в i-й связи от единичного смещения k-й связи (i, k-я дополн. связи устанавливаются в точках расположения масс m_i и m_k).

=

_ik – перемещение i-й точки системы от J_k = 1, действующей в k-й точке системы (i, k-я точки соответствуют расположению масс m_i и m_k).

L =

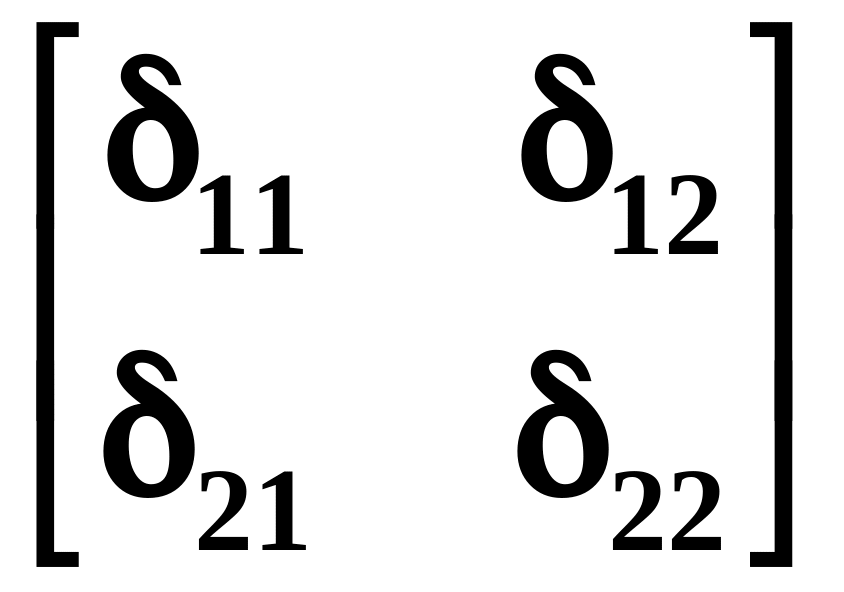
Матрица масс M. Для дискретной системы матрица масс M имеет диагональный вид:

M =

2. Статическая часть расчета: 2.1. Построение единичных эпюр

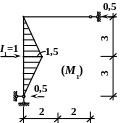
Рис. 2. Расчетная схема рамы и эпюры от действия единичных инерционных сил I_k = 1

2.2. Определение перемещений: _ij =  _ij = (M_i)(M_j)

₁₁ = (M₁)(M₁) =

= 2 31,5 1,5 = 3,34110^–5 м / кН

₁₂ = ₂₁ = (M₁)(M₂) =

= – 31,5( 2 + 2) = –3,34110^–5 м / кН

 ₂₂ = (M₂)(M₂) =

= 26 2 + 22 2 = 6,94810^–5 м / кН

3. Формирование исходных матриц уравнения (1)

М атрица податливости

L = 10^–5 м / кН

Матрица жесткости

K = кН / м

Матрица масс M = diag (m₁, m₂)

M = = 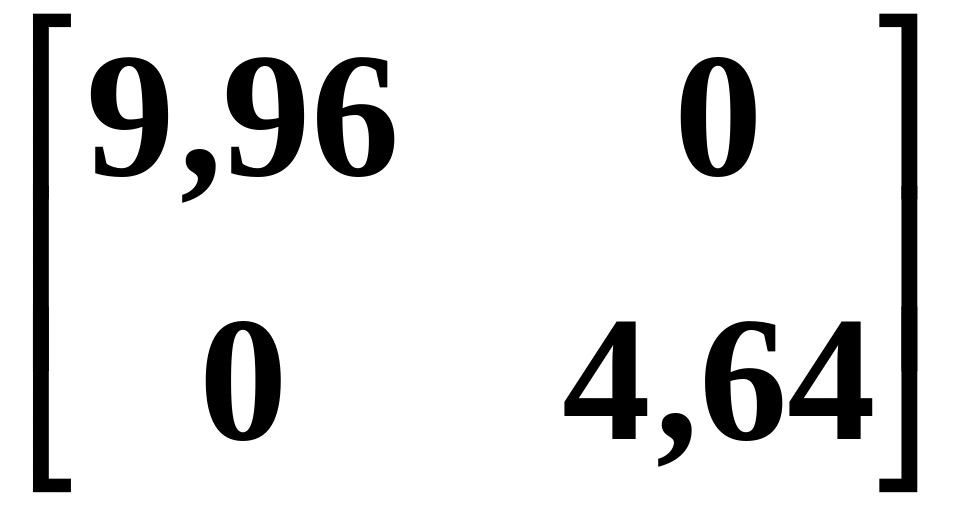кНс² / м

Построение матрицы демпфирования. Используется модель непропорционального демпфирования:

C₁ = KT, T = ,

где t_k =  ,  = / - коэффициент потерь ( = 0,07 - логарифмический декремент колебаний);  = 0,07/ = 0.0223:

t₁ = 0.0223 = 0.292910^-3 с, t₂ = 0.0223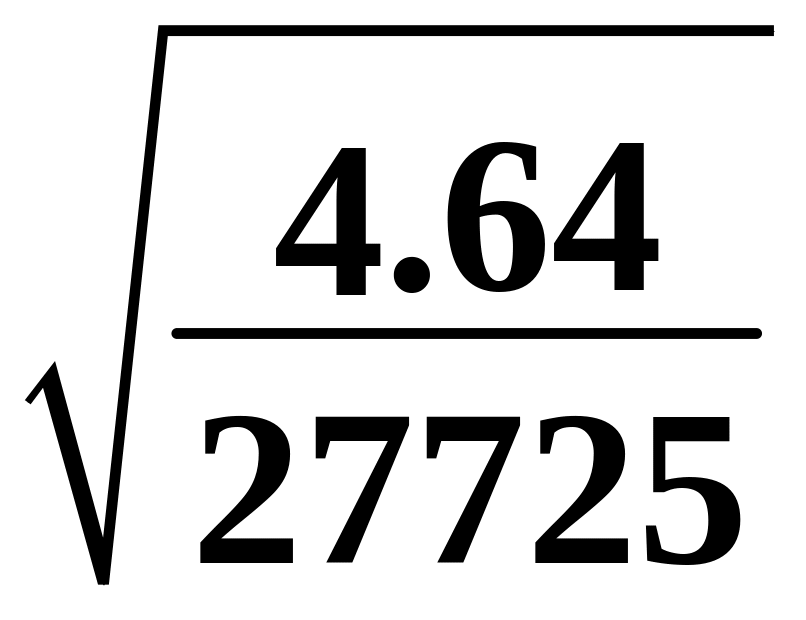 = 0.288310^-3 с.

Матрица

T = 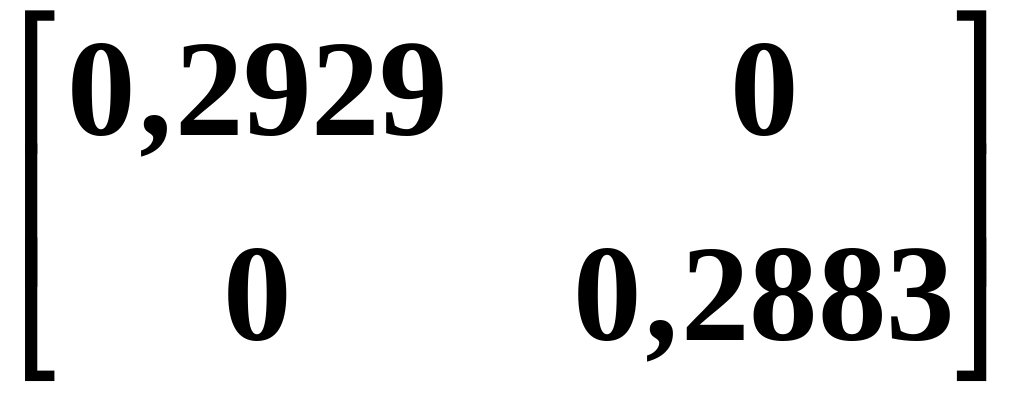10^-3 с

Матрица демпфирования C₁ = KT:

C₁ = кНс / м

Симметризация модели демпфирования C = (C₁ + C₁^T)/2

C = кНс / м

4. Алгоритм решения матричного квадратного уравнения (мку)

Найти корни характеристического МКУ, соответствующего ОДУ (1)

MS² + CS + K = 0, (2)

в котором матрицы M, C, K  M₂(R) – масс, жесткости и демпфирования имеют вид:

M =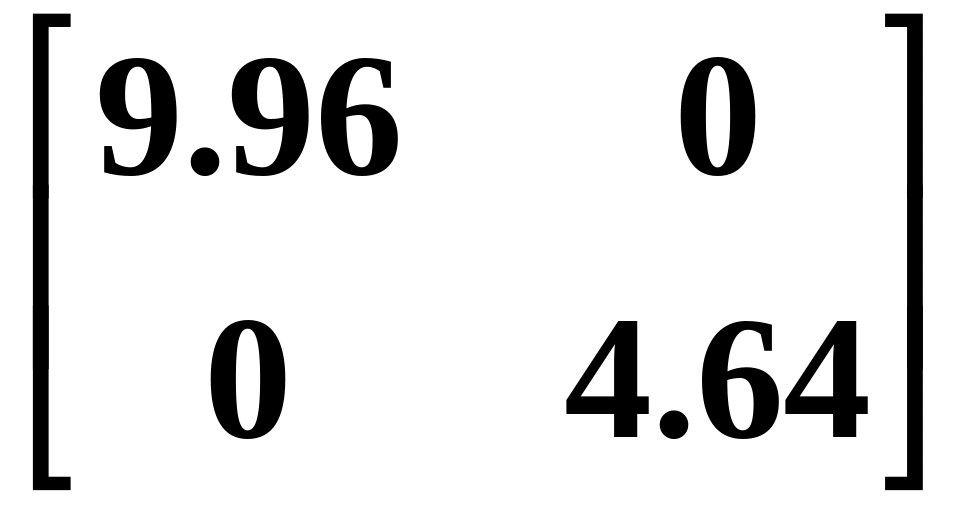 , C = , K = .

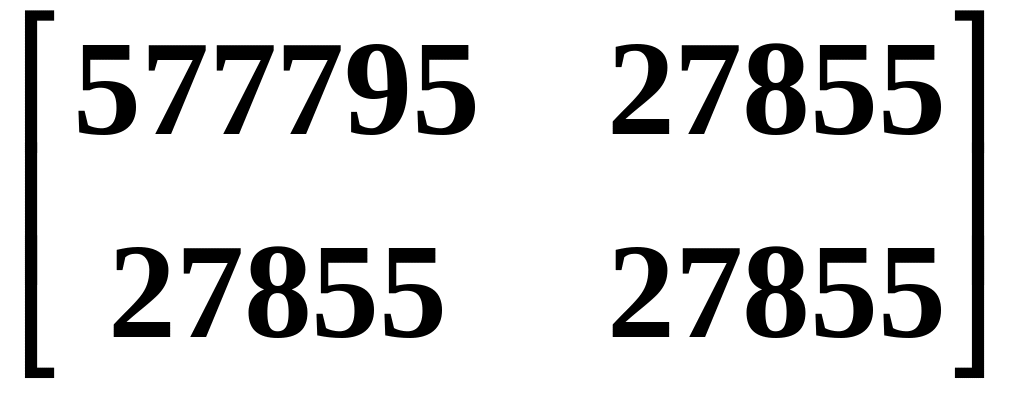Решение представляется в форме корневой пары

S₁ = S = M^–1(–C + V + U)/2,

S₂ = = M^–1(–C + V – U)/2, (3)

где V = –V^T, U = U^Т .

Система 2-х матричных уравнений, эквивалентных МКУ

U = M , (4)

(C + V)M^–1U = UM^–1(C – V), (5)

где D = 4K – (C + V)M^–1(C – V) – матрица-дискриминант МКУ.

Схема итерационного процесса для уравнений (4), (5)

U^(k) = M , D^(k) = 4K – (C + V^(k))M^–1(C – V^(k)), (4')

(C + V^(k+1))M^–1U^(k) = U^(k)M^–1(C – V^(k+1)) . (5')

Преобразование уравнения (4): (C + V)M^–1U = UM^–1(C – V) 

(6)

A^T

A

B

UM^–1V + VM^–1U = UM^–1C – CM^–1U.

Введем обозначения

(7)

A = M^–1U = , V = ,

B = UM^–1C – CM^–1U = .

После подстановки введенных обозначений в (5) получим, так называемое, Уравнение Ляпунова с к/симметрической матрицей B = –B^T в правой части:

A^TV + VA = B (6)

Система уравнений, подготовленная для итераций

U^(k) = M , D^(k) = 4K – (C + V^(k))M^–1(C – V^(k)), (8)

(A^(k))^TV^(k+1) + V^(k+1)A^(k) = B^(k). (9)

Итерационная схема решений уравнений (8), (9)

В k-й итерации задается значение матрицы V^(k). После вычисления в уравнении (8) матрицы-дискриминанта D^(k) и извлечения корня квадратного из матрицы –M^–1D^(k): строится матрица U^(k). Затем на k+1-м шаге итераций формируется матричное уравнение Ляпунова (6), из которого определяется новое значение V^(k+1). Это значение снова подставляется в выражение матрицы-дискриминанта D^(k+1). Цикл повторяется.

Для 2-х степеней свободы (n = 2) уравнение Ляпунова (6) можно разрешить относительно элемента x₁ матрицы V (см. обозначения матриц (7)) в следующем виде:

x₁ = 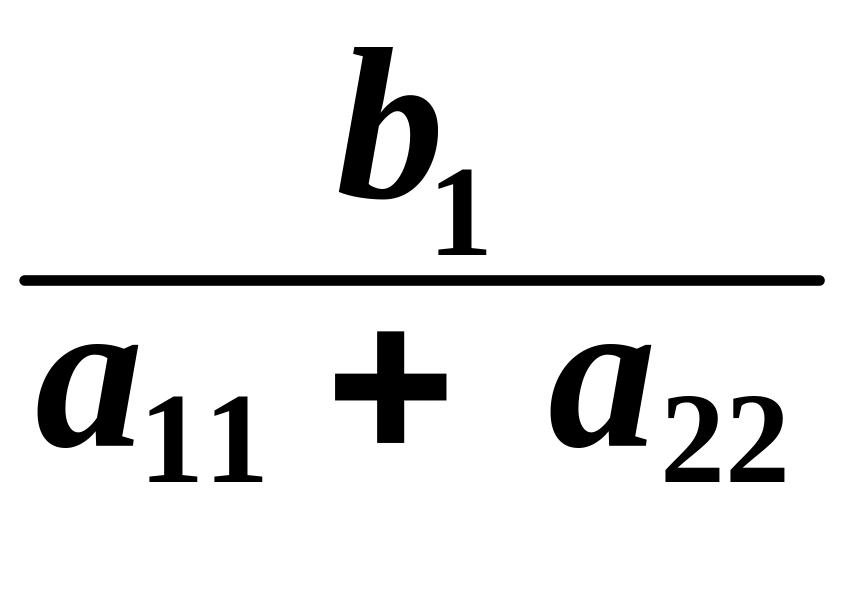. (10)

Практика 2