Пример выполнения расчетно-графической работы №2
Задача К – 1. Определить абсолютную скорость и ускорение точки М.
Дано:
;
;
t=1c;
а=0,4м; α=60°
Решение:
1. Свяжем неподвижную систему координат ОХ1У1 с пластиной. Тогда, движение точки М по прямой OD является относительным движением, а вращательное движение пластины – переносным.
2. При определении кинематических характеристик относительного движения можно мысленно остановить вращение пластины и рассматривать только движении точки согласно заданному закону.
.
В момент времен t1=1c.
.
Так как S1>0 , то точка М находится на стороне, показанной в расчетной схеме.
Найдем алгебраическую относительную скорость, и ускорение в произвольный момент времени
,
.
В момент времен t1=1c.
,
.
Знаки
показывают что вектор
и
направлены противоположно положительному
отсчету S,
покажем эти векторы.
3. При определении кинематических характеристик переносного движения, мысленно остановим точку М и рассмотрим только движение точки М1 пластины. Тогда точка М1 движется по окружности радиусом O1М1
.
Угловая скорость и угловое ускорение в произвольный момент времени равны:
,
.
В момент времен t1=1c
,
.
Знаки
указывают на то, что ускорение и скорость
направлены согласно положительному
направлению
,
следовательно, против часовой стрелки.
Определим
и
в момент времен t1=1c:
,
,
.
Изобразим векторы на чертеже.
4. Модуль ускорения Кориолиса точки определим из выражения:
,
где
- угол между вектором
и осью вращения. В момент времен t1=1c
,
откуда
.
Вектор
перпендикулярен векторам
и
,
так что кратчайший поворот
до совмещения с вектором
,
виден с конца вектора
против часовой стрелки.
5.
Векторы
и
определяются по формулам:
,
.
Для определения векторов абсолютных скоростей и ускорений воспользуемся аналитическим методом, проведя координатные оси М1ХУ.
Запишем равенство в проекции на эти оси и определим абсолютную скорость.
,
откуда
,
,
,
.
Запишем
теперь равенство
в проекциях на оси координат и определим
абсолютное ускорение в момент времени
t1=1c:
,
,
.
Ответ:
;
;
;
.
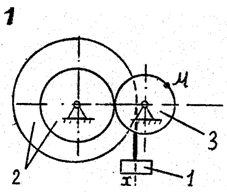
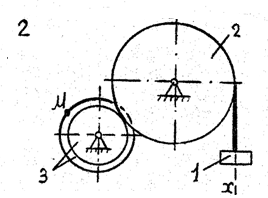
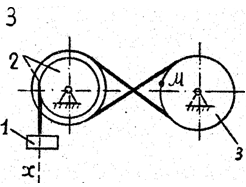
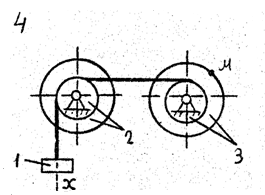
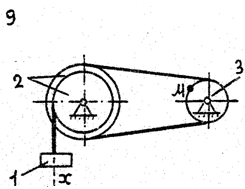
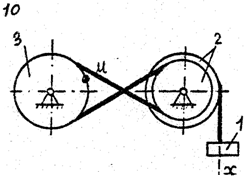
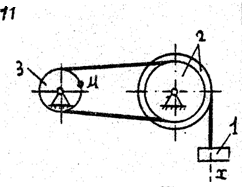
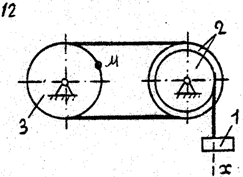
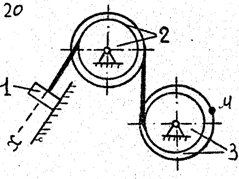
Задача к – 2
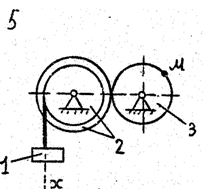
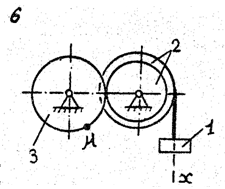
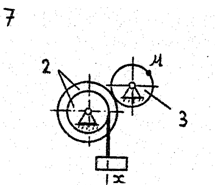
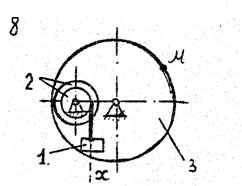
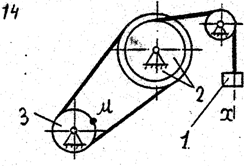
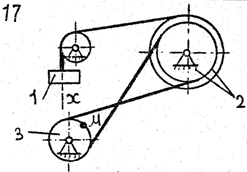
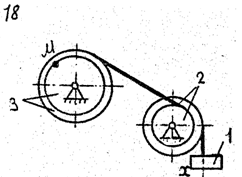
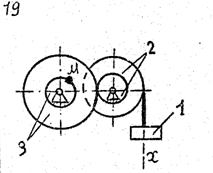
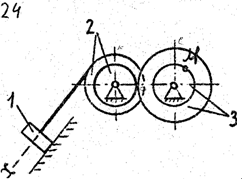
По данному уравнению прямолинейного поступательного движения груза 1 определить скорость, касательное, нормальное и полное ускорение точки М механизма в момент времени, когда путь, пройденный грузом, равен S.
VII. Данные к задаче К – 2
1 цифра шифра |
R2, м |
r2,м |
R3,м |
r3, м |
2-я цифра шифра |
x=x(t) (x, м; t, с) |
S,м |
1 |
0,1 |
0,08 |
0,2 |
0,1 |
1 |
0,08+0,4 |
0,1 |
2 |
0,2 |
0,16 |
0,3 |
0,25 |
2 |
0,05+0,6 |
0,2 |
3 |
0,3 |
0,25 |
0,4 |
0,3 |
3 |
0,03+0,6 |
0,3 |
4 |
0,4 |
0,3 |
0,3 |
0,15 |
4 |
0,03+0,4 |
0,6 |
5 |
0,5 |
0,45 |
0,4 |
0,2 |
5 |
0,7 |
0,5 |
6 |
0,6 |
0,5 |
0,5 |
0,4 |
6 |
0,03+0,3 |
0,4 |
7 |
0,7 |
0,5 |
0,5 |
0,15 |
7 |
0,5 |
0,25 |
8 |
0,6 |
0,4 |
0,4 |
0,25 |
8 |
0,02+0,5 |
0,3 |
9 |
0,5 |
0,35 |
0,6 |
0.35 |
9 |
0,07+0,9 |
0,7 |
0 |
0.4 |
0,25 |
0,5 |
0,45 |
0 |
0,03+0,7 |
0,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
