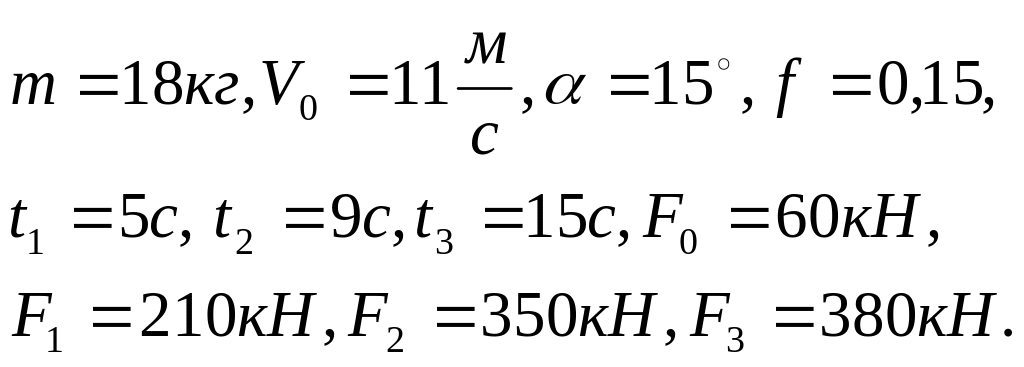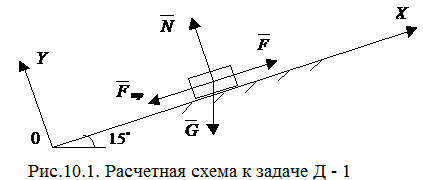
Пример выполнения расчетно-графической работы №3
Задача
Д-1. Телу массой m сообщена начальная
скорость
направленная вверх по наклонной
плоскости, составляющей угол α с
горизонтом, на тело действует сила
,
направленная в туже сторону. Зная закон
изменения силы
и коэффициентом трения скольжения
, определить скорость тела в моменты
времени
и проверить полученный результат для
момента времени
с помощью дифференцированного
уравнения движения.
|
Дано:
|
Решение:
По теореме об изменении количества движения имеем
,
где
- проекции скорости в начале участка на
оси координат,
- проекции скорости в момент времени
,
(очевидно
).
-
сумма проекций импульсов сил, действующих
на тело, на ось OX;
-
сумма проекций импульсов сил на ось OY.
=>
Обозначим
,
тогда уравнение принимает вид:
.
Полученное
уравнение можно применит к каждому
участку если считать, что
-
скорость тела в начале рассматриваемого
участка,
-время,
отсчитываемое от начала рассматриваемого
участка.
1) Участок №1
Здесь
- зависимость силы F
от времени t.
Но при t=5
с
,
то есть
Находим импульс силы F.
Уравнение
принимает вид:
Проверим,
возможно ли остановить тела на этом
участке. Находим дискриминант квадратного
трехчлена
следовательно, при любых t
и значит останов невозможен. t=5c
находим
2) Участок №2
Здесь
при
.
Уравнение
имеет вид:
.
Здесь очевидно VX>0 при любых t, т.е. останов невозможен. При t=4c. Находим:
.
3) Участок №3
Здесь
.
Уравнение имеет вид:
.
Дифференциальное уравнение движения тела на первом участке имеет вид:
,
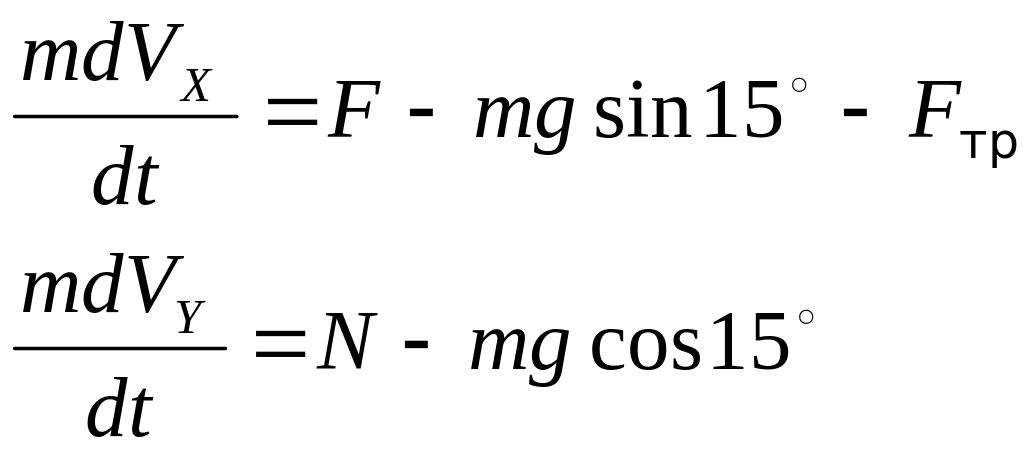
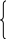Делим
на m
и
вводим обозначение
Получаем
Интегрируя в пределах от 0 до t, получаем уравнение:
или
.
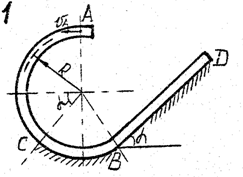
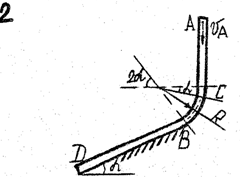
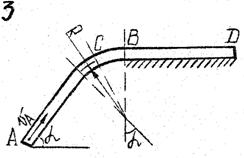
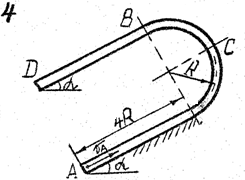
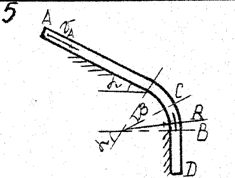
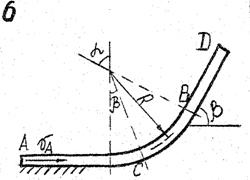
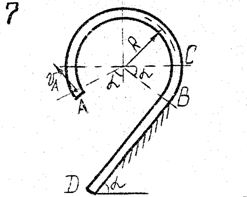
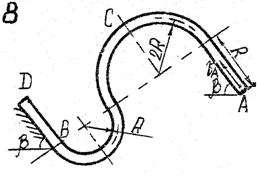
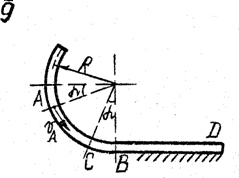
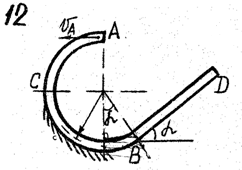
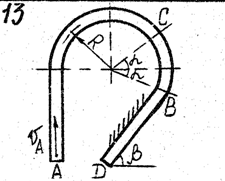
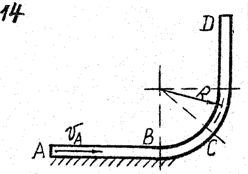
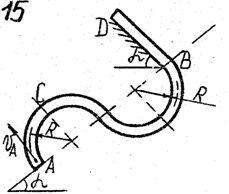
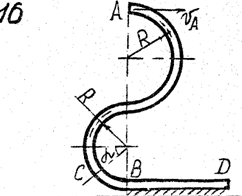
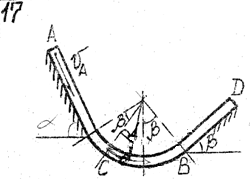
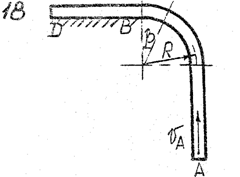
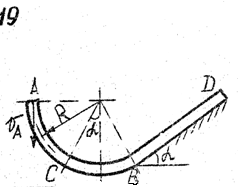
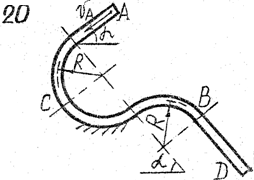
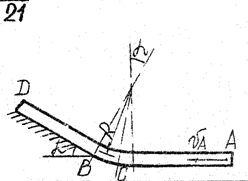
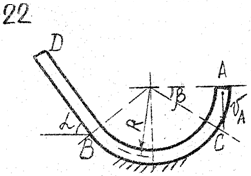
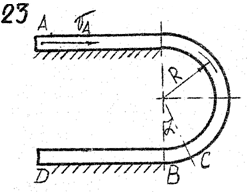
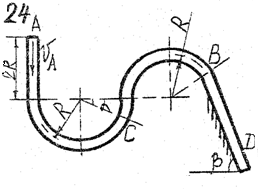
Задача д – 2
Шарик, принимаемый за материальную точку, движется из положения А внутри трубки в вертикальной плоскости. Найти скорость шарика в положениях В и С. Определить время движения шарика до точки D или до остановки. (Отсутствующими размерами трубки задаться).
XI. Данные к задаче Д – 1
1-ая цифра шифра |
m, кг |
VA, м/с |
R, м |
BD, м |
2-ая цифра шифра |
|
|
1 |
0,5 |
0,9 |
0,4 |
0,6 |
1 |
45 |
30 |
2 |
0,4 |
0,8 |
0,3 |
0,7 |
2 |
50 |
25 |
3 |
0,3 |
0,7 |
0,2 |
0,8 |
3 |
60 |
40 |
4 |
0,6 |
0,5 |
0,6 |
0,9 |
4 |
70 |
50 |
5 |
0,7 |
0,6 |
0,5 |
1,0 |
5 |
60 |
30 |
6 |
0,8 |
0,4 |
0,3 |
0,9 |
6 |
50 |
25 |
7 |
0,2 |
0,3 |
0,4 |
0,7 |
7 |
45 |
20 |
8 |
0,5 |
0,2 |
0,3 |
0,8 |
8 |
60 |
40 |
9 |
0,6 |
0,8 |
0,2 |
0,6 |
9 |
50 |
20 |
0 |
0,7 |
0,5 |
0,3 |
0,7 |
0 |
45 |
15 |
,
град
,
град
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
