
- •Методические указания и контрольные задания по высшей математике
- •Методические указания и контрольные задания по высшей математике
- •Общие методические указания
- •Указания к выполнению контрольных работ Тема 1. Элементы аналитической геометрии на плоскости
- •Примеры решения задач
- •Тема 2. Основы векторной алгебры
- •Тема 3. Элементы аналитической геометрии в пространстве
- •Тема 4. Элементы линейной алгебры
- •Тема 5. Введение в анализ
- •Тема 6 Производная и дифференциал
- •Тема 7. Исследование поведения функции
- •Тема 8. Неопределенный интеграл
- •Тема 9. Определенный интеграл
- •Тема 10. Приложения определенного интеграла
- •Тема 11. Функции нескольких переменных
- •Тема 12. Кратные интегралы. Криволинейный интеграл.
- •Тема 13. Ряды и их приложения.
- •Тема 14. Дифференциальные уравнения первого порядка
- •Тема 15. Дифференциальные уравнения второго порядка
- •Тема 16. Основы теории вероятностей
- •Задачи для контрольных работ
- •Приложение
- •Литература
- •Содержание
- •Тема 1. Элементы аналитической геометрии на плоскости 9
Тема 14. Дифференциальные уравнения первого порядка
Пискунов, гл. X111, §1—4, упр. 1 – 5, 9—23, 26,27, 29, 33, 35; §5, упр. 39—44, 46; § 7, 8, упр. 57—68. Разберите решения задач 32, 33 из данного пособия.
Задача 32.
Найти общее
решение уравнения
![]() .
.
Решение:
Данное уравнение является однородным,
так как коэффициенты при
![]() и
и
![]() есть однородные функции одного и того
же измерения (второго) относительно
переменных
есть однородные функции одного и того
же измерения (второго) относительно
переменных
![]() .
Применяем подстановку
.
Применяем подстановку
![]() ,
где
,
где
![]() –
некоторая функция аргумента
–
некоторая функция аргумента
![]() .
.
Если
![]() ,
то дифференциал
,
то дифференциал
![]() ,
и данное уравнение примет вид
,
и данное уравнение примет вид
![]() .
.
Сократив на
![]() ,
будем иметь:
,
будем иметь:
![]() ;
;
![]() ;
;
![]()
![]() ;
;
![]() ;
;
![]() .
.
Мы получили уравнение с разделенными переменными относительно и . Интегрируя, находим общее решение этого уравнения:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Потенцируя, находим
![]() ,
или
,
или
![]() .
Из введенной подстановки следует, что
.
Из введенной подстановки следует, что
![]() .
Следовательно,
.
Следовательно,
![]() или
или
![]() – общее решение данного уравнения.
– общее решение данного уравнения.
Задача 33.
Найти общее
решение уравнения
![]() .
.
Решение:
Данное уравнение является линейным,
так как оно содержит искомую функцию
![]() и её производную
и её производную
![]() в первой степени и не содержит их
произведений.
в первой степени и не содержит их
произведений.
Применяем
подстановку
![]() ,
где
,
где
![]() и
и
![]() - некоторые неизвестные функции аргумента
.
Если
,
то
- некоторые неизвестные функции аргумента
.
Если
,
то
![]() и данное уравнение примет вид
и данное уравнение примет вид
![]() ,
,
или
![]() .
(1)
.
(1)
Так как искомая функция представлена в виде произведения двух других неизвестных функций, то одну из них можно выбрать произвольно. Выберем функцию так, чтобы выражение, стоящее в круглых скобках левой части равенства (1), обращалось в нуль, т.е. выберем функцию так, чтобы имело место равенство
![]() (2)
(2)
При таком выборе функции уравнение (1) примет вид
![]() .
(3)
.
(3)
Уравнение (2) есть уравнение с разделяющимися переменными относительно и . Решим это уравнение:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ,
,
![]() .
.
Чтобы равенство
(2) имело место, достаточно найти одно
какое – либо частное решение,
удовлетворяющее этому уравнению. Поэтому
для простоты при интегрировании этого
уравнения находим то частное решение,
которое соответствует значению
произвольной постоянной С=0. Подставив
в (3) найденное выражение для
![]() ,
получим:
,
получим:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
Интегрируя, получаем
.
Интегрируя, получаем
![]() .
Тогда
.
Тогда
![]() - общее решение данного уравнения.
- общее решение данного уравнения.
Тема 15. Дифференциальные уравнения второго порядка
Пискунов, гл. X111, §16—18, упр. 118, 121—124; §20-22, упр. 129—134, 136; §23, 24, упр. 148—157, 38—40; § 25, упр. 141. 158. Разберите решения задачи 34-37 из данного пособия.
Задача 34.
Дано уравнение:
![]() .
Найти частное решение, удовлетворяющее
начальным условиям:
.
Найти частное решение, удовлетворяющее
начальным условиям:
![]() ;
;
![]() .
.
Решение:
Данное дифференциальное уравнение
второго порядка не содержит явно функцию
![]() .
Положим
.
Положим
![]() ,
где
,
где
![]() - некоторая функция аргумента
.
Если
,
то
- некоторая функция аргумента
.
Если
,
то
![]() и данное уравнение примет вид
и данное уравнение примет вид
![]() .
Мы получили уравнение первого порядка
относительно переменных
и
.
Решим это уравнение:
.
Мы получили уравнение первого порядка
относительно переменных
и
.
Решим это уравнение:
![]() ;
;
![]() ;
;
![]() ,
,
откуда
![]() или
или
![]() .
.
Определим численное
значение
![]() при указанных начальных условиях. Имеем
при указанных начальных условиях. Имеем
![]() .
Следовательно,
.
Следовательно,
![]() .
Теперь решаем уравнение первого порядка
.
Теперь решаем уравнение первого порядка
![]() :
:
![]() ;
;
![]() .
.
Определим численное
значение
![]() при указанных начальных условиях. Имеем
при указанных начальных условиях. Имеем
![]() ;
;
![]() .
.
Таким образом,
![]() есть частное решение, удовлетворяющее
указанным начальным условиям.
есть частное решение, удовлетворяющее
указанным начальным условиям.
Задача 35.
Дано уравнение
![]() .
Найти частное решение, удовлетворяющее
начальным условиям:
.
Найти частное решение, удовлетворяющее
начальным условиям:
![]() ;
;
![]() .
.
Решение:
Данное уравнение второго порядка не
содержит явно аргумента
.
Положим
![]() ,
,
![]() – некоторая функция аргумента
.
Если
– некоторая функция аргумента
.
Если
,
то
 .
Тогда данное уравнение примет вид
.
Тогда данное уравнение примет вид
![]() ;
;
![]() ;
;
![]() .
.
Если приравнять
нулю первый множитель, то получаем:
![]() ;
;
![]() ;
;
![]() - решение данного уравнения.
- решение данного уравнения.
Приравняем нулю второй множитель:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ,
или
,
или
![]() .
.
Используя начальные
условия, находим
![]() :
:
![]() ;
;
![]() .
.
Далее решаем
уравнение
![]() :
:
![]() ;
;
![]() .
.
Теперь определим значение :
![]() ;
;
![]() .
.
Тогда
![]() ;
;
![]() и
и
![]() - искомое частное решение, удовлетворяющее
указанным начальным условиям.
- искомое частное решение, удовлетворяющее
указанным начальным условиям.
Задача 36. Решить систему уравнений и выделить частные решения, удовлетворяющие заданным начальным условиям:
 ,
,
![]() ,
,
![]() .
.
Решение:
Обе части первого уравнения системы
продифференцируем по переменной
![]() :
:
![]() .
.
В полученном
уравнении заменим
![]() правой частью второго уравнения системы.
В результате получим неоднородное
линейное уравнение второго порядка:
правой частью второго уравнения системы.
В результате получим неоднородное
линейное уравнение второго порядка:
![]() (1)
(1)
Составим и решим соответствующее однородное линейное уравнение:
![]() (2)
(2)
Характеристическое
уравнение
![]() имеет корни:
имеет корни:
![]() ,
,
![]() .
Следовательно, общее решение (2) имеет
вид
.
Следовательно, общее решение (2) имеет
вид
![]() .
.
Находим частное
решение
![]() .
Дважды дифференцируя, получим
.
Дважды дифференцируя, получим
![]() ,
,
![]() .
Подставив в (1) , находим
.
Подставив в (1) , находим
![]() .
Следовательно,
.
Следовательно,
![]() и
и
![]() .
(3)
.
(3)
Из первого уравнения
системы находим, что
![]() ,
или
,
или
![]() ,
откуда
,
откуда![]() .
(4)
.
(4)
Подставив начальные условия в (3) и (4), получим систему
![]()
Решение этой
системы дает
![]() и
и
![]() .
Следовательно,
.
Следовательно,
![]() и
и
![]() – частные решения, удовлетворяющие
заданным начальным условиям.
– частные решения, удовлетворяющие
заданным начальным условиям.
Задача 37. Найти частные решения неоднородных дифференциальных уравнений второго порядка с постоянными коэффициентами со специальной правой частью, удовлетворяющее указанным начальным условиям:
а) ![]()
![]() ;
б)
;
б) ![]()
![]() .
.
При
решении данных уравнений удобно
использовать следующий алгоритм. Если
дано неоднородное дифференциальное
уравнение второго порядка с постоянными
коэффициентами со специальной правой
частью
![]() где
где
![]()
![]() ,
где
,
где
![]() -
многочлен степени
-
многочлен степени
![]() ,
,
![]() -
многочлен степени
-
многочлен степени
![]() .
Тогда общее решение уравнения ищется
в виде
.
Тогда общее решение уравнения ищется
в виде
![]() ,
где
,
где
![]() -
общее решение соответствующего
однородного уравнения,
-
общее решение соответствующего
однородного уравнения,
![]() -
какое-либо частное решение неоднородного
уравнения.
-
какое-либо частное решение неоднородного
уравнения.
Чтобы найти - общее решение соответствующего однородного уравнения
 составляем характеристическое уравнение
составляем характеристическое уравнение
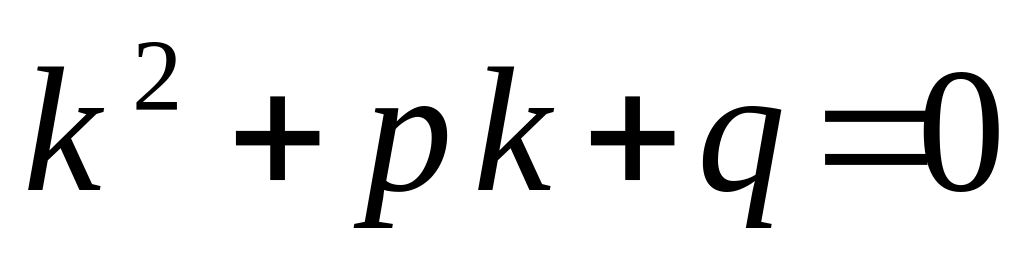 .
При решении которого возможны следующие
случаи:
.
При решении которого возможны следующие
случаи:
уравнение имеет действительные различные корни
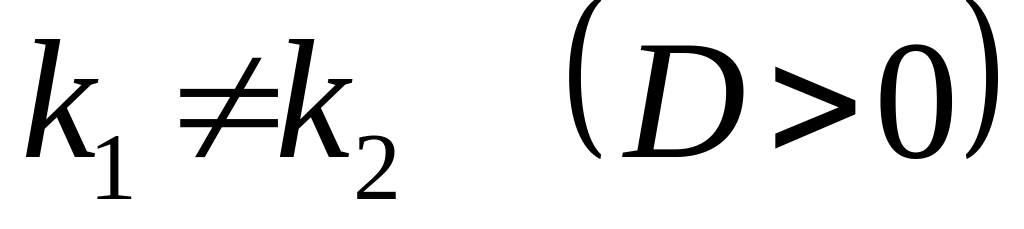 ,
тогда
,
тогда
 ,
где
,
где
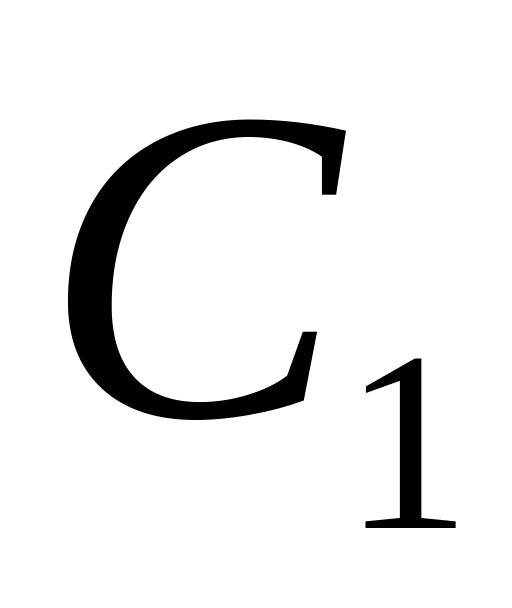 и
и
 -
произвольные постоянные;
-
произвольные постоянные;уравнение имеет действительные равные корни
 ,
тогда
,
тогда
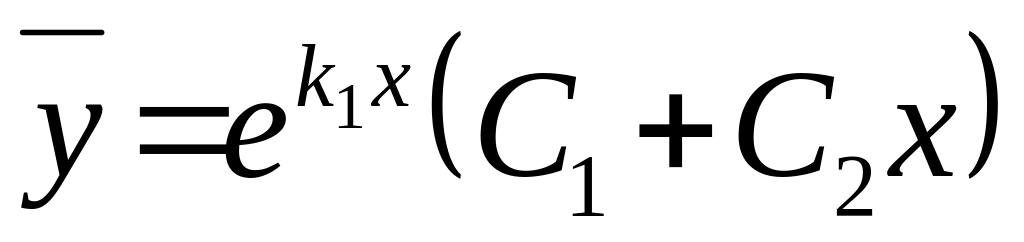 ,
где
и
-
произвольные постоянные;
,
где
и
-
произвольные постоянные;уравнение имеет комплексные корни
 и
и
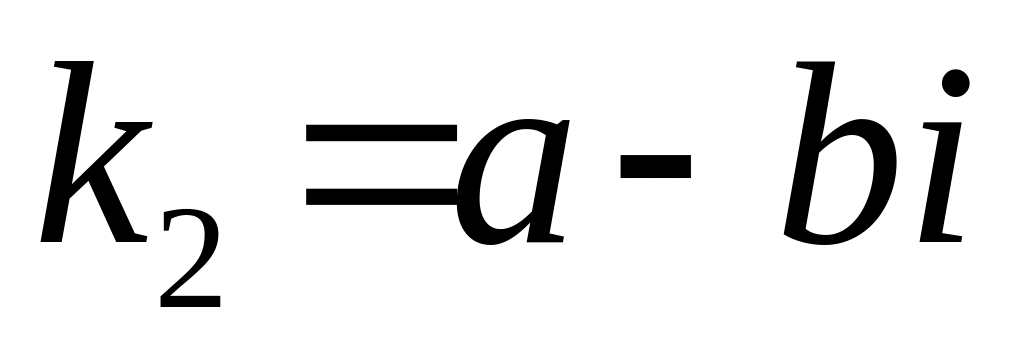
 ,
тогда
,
тогда
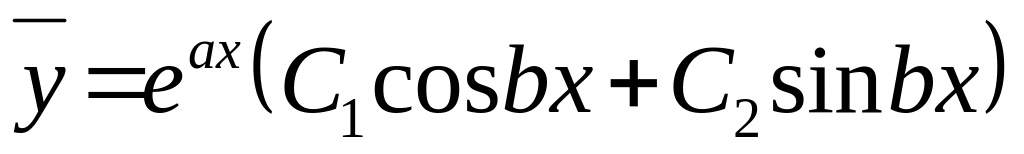 ,
где
и
-
произвольные постоянные.
,
где
и
-
произвольные постоянные.
Если правая часть уравнения
 имеет специальный вид
имеет специальный вид
 ,
где
,
где
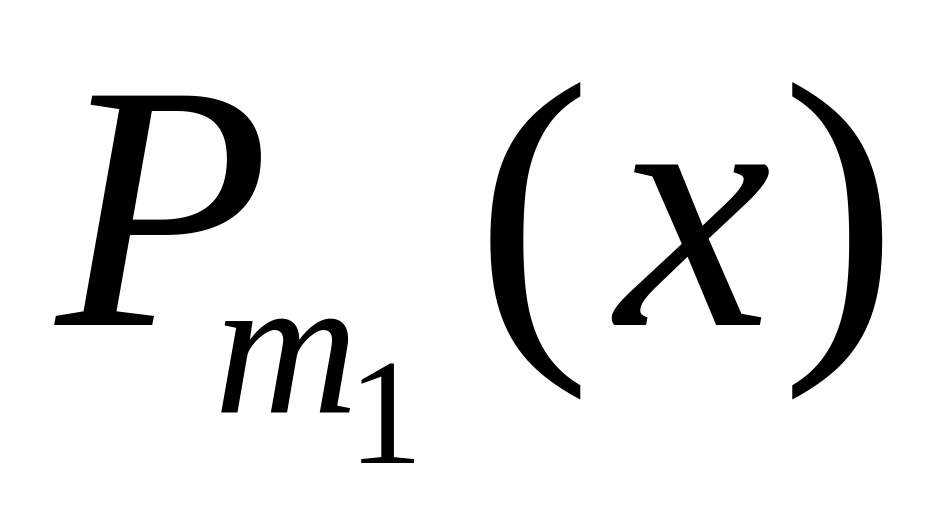 -
многочлен степени
,
-
многочлен степени
,
тогда частное решение
ищется в виде:
-
многочлен степени
,
-
многочлен степени
,
тогда частное решение
ищется в виде:
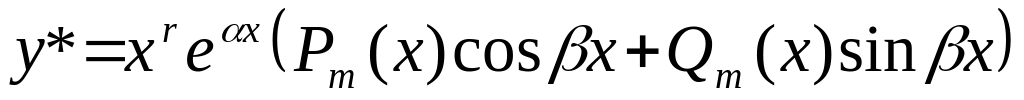 ,
,
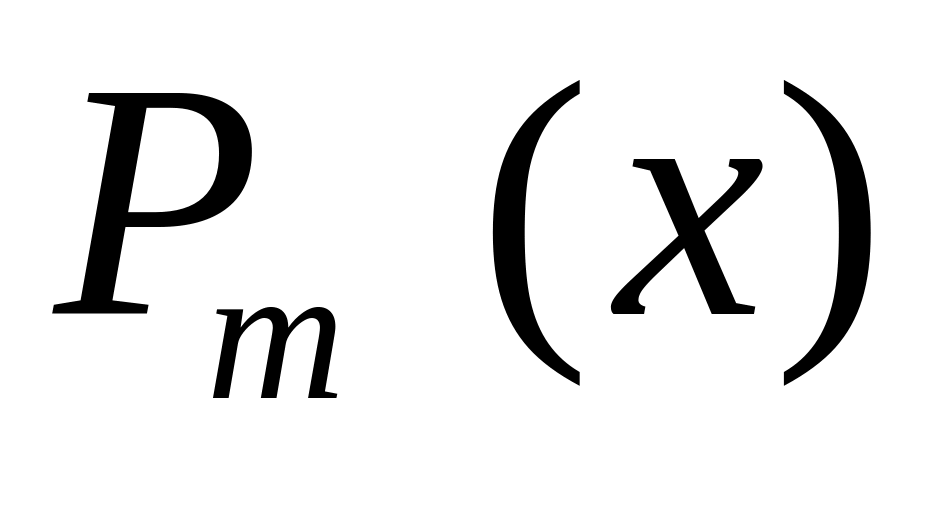 и
и
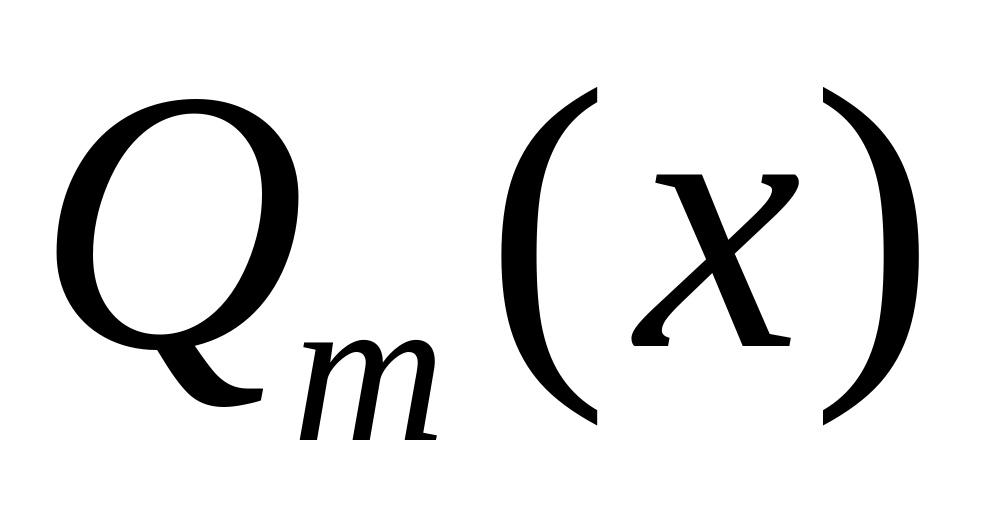 -
многочлены степени
-
многочлены степени
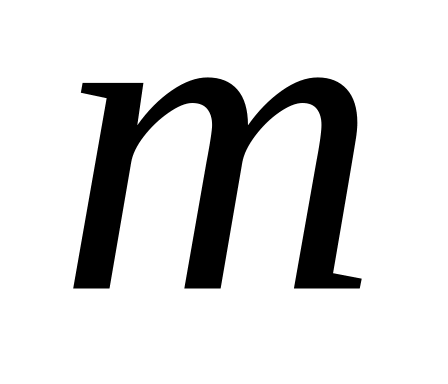 ,
,
 ,
а
,
а
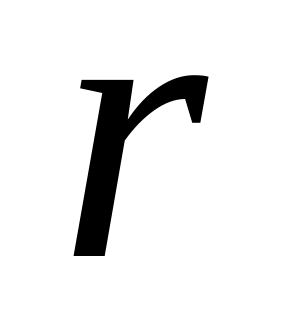 - кратность корня
- кратность корня
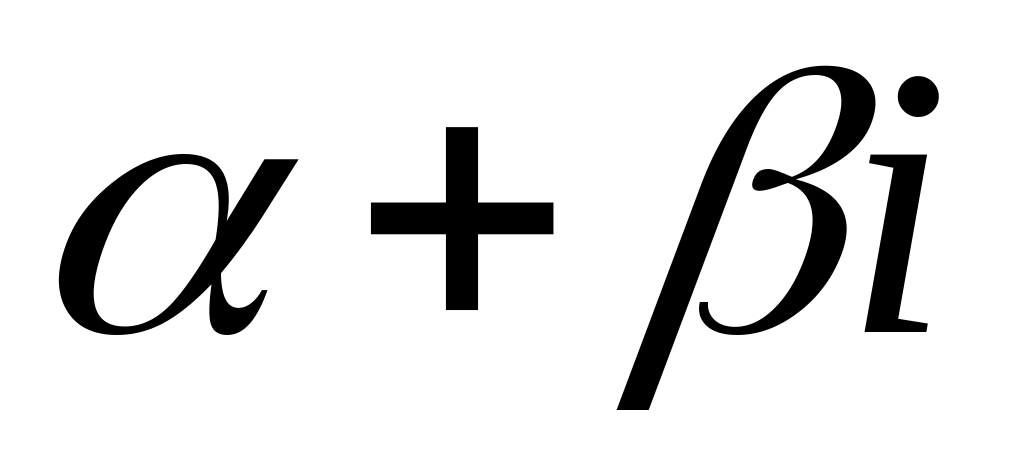 характеристического уравнения
.
характеристического уравнения
.
При составлении частного решения удобно использовать следующую таблицу:
Степень многочлена |
Вид многочлена |
Вид многочлена |
|
|
|
=1 |
|
|
=2 |
|
|
=3 |
|
|
Решение: а) .
Общее решение
данного уравнения имеет вид:
![]() .
.
Найдём
.
Для этого решим соответствующее
однородное уравнение
![]() .
Составляем характеристическое уравнение:
.
Составляем характеристическое уравнение:
![]() .
Корнями этого уравнения являются
.
Корнями этого уравнения являются
![]() и
и
![]() .
Т.к. решения действительные различные
числа (первый случай), то
.
Т.к. решения действительные различные
числа (первый случай), то
![]() или
или
![]() .
.
Теперь
найдём
.
Правая часть
![]() имеет специальный вид, причём
=2,
=0,
значит
имеет специальный вид, причём
=2,
=0,
значит
![]() ,
,
![]() =0,
=0,
![]() =0,
тогда
=0,
тогда
![]() и
,
т.о.
=1.
и
,
т.о.
=1.
Получаем:
![]() ,
т.к.
,
т.к.
![]() ,
,
![]() =1,
=1,
![]() =0,
то
=0,
то
![]() ,
,
![]() .
Найдём производные первого и второго
порядка от
.
.
Найдём производные первого и второго
порядка от
.
![]() ,
,
![]() .
Запишем
,
.
Запишем
,
![]() и
и
![]() следующим образом, подписывая слева
коэффициенты
следующим образом, подписывая слева
коэффициенты
![]() ,
и
,
и
![]() из
исходного уравнения:
из
исходного уравнения:

Далее приравниваем коэффициенты при соответствующих степенях :


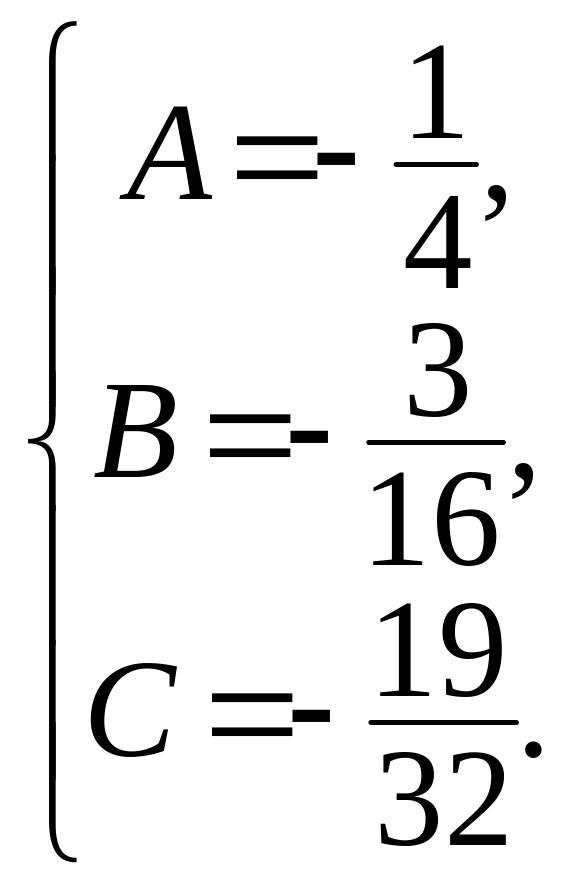
Тогда
![]() .
Следовательно, общее решение исходного
уравнения:
.
Следовательно, общее решение исходного
уравнения:
![]() .
Чтобы найти частное решение, удовлетворяющее
начальным условиям, найдём
:
.
Чтобы найти частное решение, удовлетворяющее
начальным условиям, найдём
:
![]() .
.
Подставляем начальные условия в и .
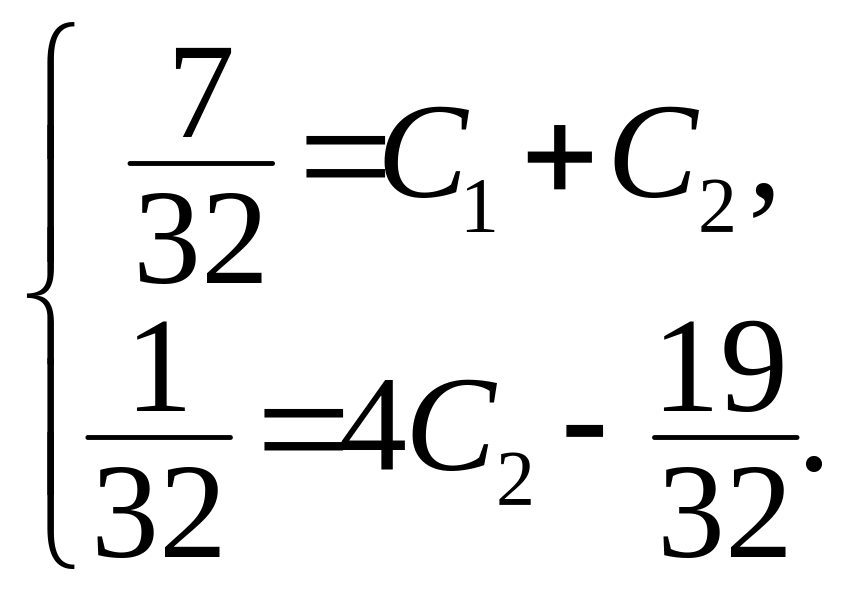 Отсюда
Отсюда
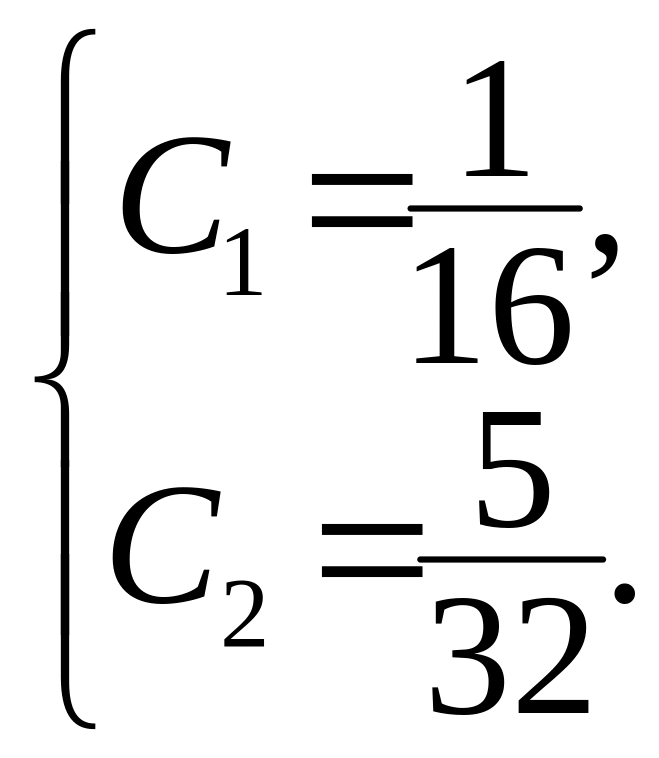
Тогда
![]() -частное
решение исходного уравнения.
-частное
решение исходного уравнения.
б)
Общее решение данного уравнения имеет вид: .
Найдём
.
Для этого решим соответствующее
однородное уравнение
![]() .
Составляем характеристическое уравнение:
.
Составляем характеристическое уравнение:
![]() ,
,
![]() .
Корнями этого уравнения являются
.
Корнями этого уравнения являются
![]() и
и
![]() .
Т.к. решения комплексные числа (третий
случай), то
.
Т.к. решения комплексные числа (третий
случай), то
![]() или
или
![]() .
.
Теперь
найдём
.
Правая часть
![]() есть сумма двух функций, имеющих
специальный вид:
есть сумма двух функций, имеющих
специальный вид:
![]() ,
где
,
где
![]() и
и
![]() .
Тогда
.
Тогда
![]() .
.
Рассмотрим
.
Имеем
=0,
=0,
значит
![]() ,
=3,
=0,
тогда
,
=3,
=0,
тогда
![]() не совпадает ни с одним из корней
характеристического уравнения, т.о.
не совпадает ни с одним из корней
характеристического уравнения, т.о.
![]() =0.
=0.
Получаем:
![]() ,
т.к.
,
т.к.
![]() ,
,
![]() =1,
=0,
то
=1,
=0,
то
![]() .
.
Рассмотрим
.
Имеем
=0,
=0,
значит
![]() ,
=0,
=2,
тогда
,
=0,
=2,
тогда
![]() не совпадает ни с одним из корней
характеристического уравнения, т.о.
=0.
не совпадает ни с одним из корней
характеристического уравнения, т.о.
=0.
Получаем:
![]() ,
т.к.
,
,
т.к.
,
![]() =1,
то
=1,
то
![]() .
.
Тогда
![]() .
Найдём производные первого и второго
порядка от
.
.
Найдём производные первого и второго
порядка от
.
![]() ,
,
![]() .
Запишем
,
и
.
Запишем
,
и
![]() следующим образом, подписывая слева
коэффициенты
,
и
из
исходного уравнения:
следующим образом, подписывая слева
коэффициенты
,
и
из
исходного уравнения:

Далее приравниваем коэффициенты при соответствующих подобных слагаемых:



Тогда
![]() .
Следовательно, общее решение исходного
уравнения:
.
Следовательно, общее решение исходного
уравнения:
![]() .
Чтобы найти частное решение, удовлетворяющее
начальным условиям, найдём
:
.
Чтобы найти частное решение, удовлетворяющее
начальным условиям, найдём
:
![]() .
Подставляем начальные условия
в
и
.
.
Подставляем начальные условия
в
и
.
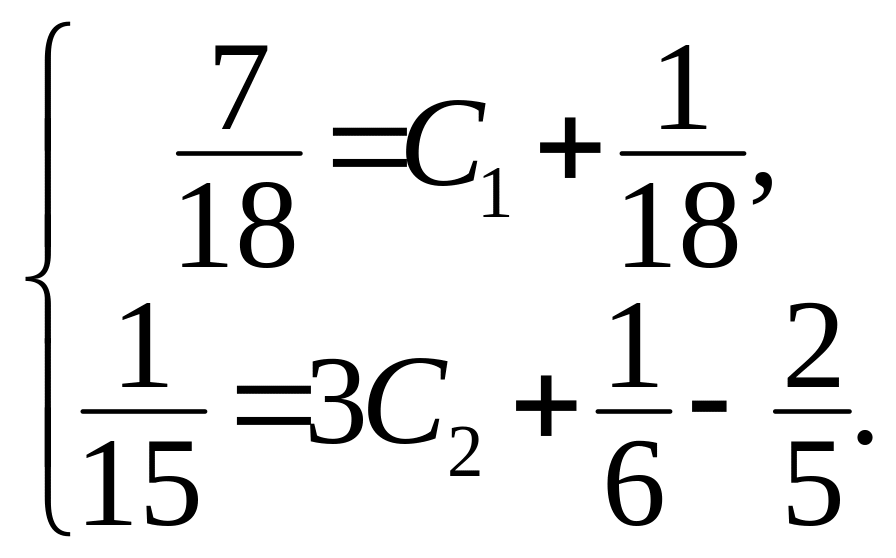 Отсюда
Отсюда

Тогда
![]() -
частное решение исходного уравнения.
-
частное решение исходного уравнения.
