Тема 12. Кратные интегралы. Криволинейный интеграл.
Пискунов, гл. XIV, §1—3, упр. 1 – 6, 8—16; §4, упр. 24—29, 31 — 36; §5, упр. 18—20, 38—40; § 7, упр. 43—47; § 8—10, упр. 51—54, 57, 64; § 11—14, упр. 65—68. Гл. XV, § 1—2 упр. 1—5. Разберите решения задачи 28 из данного пособия.
Задача 28.
Дан интеграл
Т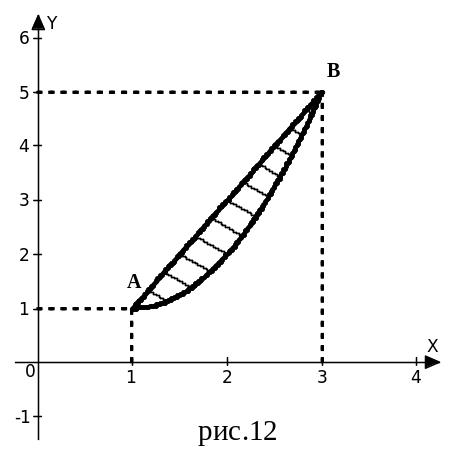
ребуется:
1) построить на плоскости хОу область интегрирования D;
2) изменить порядок интегрирования;
3) вычислить площадь области D при заданном и измененном порядке интегрирования.
Решение:
1. Пределы внешнего интеграла по переменной х — числа 1 и 3 — указывают на то, что область D ограничена слева прямой х = 1 и справа прямой х = 3.
Пределы
внутреннего интеграла по переменной у
указывают
на то, что область D
ограничена
снизу
параболой
и сверху прямой
Построив эти линии на отрезке [1; 3],
получим область D
(рис.
12).
2. Чтобы изменить порядок интегрирования, установим пределы интегрирования для внешнего интеграла по переменной у. Как видно из рис. 12 наименьшее значение, которое принимает у в области D, равно 1 в точке А(1; 1), а наибольшее значение равно 5 в точке В(3; 5). Следовательно, внешний интеграл по переменной у будет иметь пределы: 1 (нижний предел) и 5 (верхний предел).
Определим пределы для внутреннего интеграла по переменной х.
Из
уравнения прямой
получаем
нижний предел.
Из
уравнения параболы
получаем
– верхний предел. Таким образом,
3. Вычислим площадь области D при заданном порядке интегрирования:
4. Вычислим площадь области D при измененном порядке интегрирования:
Тема 13. Ряды и их приложения.
Минорский№2422, 2425, 2432, 2438, 2444, 2470, 2473, 2492, 2525, 2533.
Разберите решения задач 29-31 из данного пособия.
Задача 29.
Найти область
сходимости степенного ряда
.
Решение: Данный степенной ряд можно записать так:
Применяем признак Даламбера:
Ряд будет сходиться
для тех значений х, для которых
.
Определим сходимость на концах интервала. При х= –2/3 ряд примет вид:
Этот ряд является
знакочередующимся; его общий член по
абсолютному значению стремится к нулю
при
.
По признаку Лейбница о сходимости
знакочередующихся рядов заключаем, что
этот ряд сходится. Следовательно,
значение х = - 2/3 принадлежит области
сходимости данного ряда.
Подставив х = 2/3, получим
Этот ряд расходится,
так как каждый член этого ряда начиная
со второго больше соответствующего
члена гармонического ряда. Следовательно,
значение х = 2/3 не принадлежит области
сходимости данного ряда. Таким образом,
– область сходимости исследуемого
ряда.
Задача 30.
Вычислить
интеграл
с точностью до 0,001.
Решение: Предварительно представим подынтегральную функцию в виде степенного ряда. Используя известное разложение в степенной ряд Маклорена функции sinx, имеем:
, тогда
Мы получили знакочередующийся ряд, который удовлетворяет условиям теоремы Лейбница. Так как в полученном ряде четвертый член по абсолютному значению меньше 0,001, то ограничиваемся только первыми тремя членами.
Задача 31.
Найти первые три (отличные от нуля) члена
разложения в степенной ряд Маклорена
функции у(х), являющейся частным решением
дифференциального уравнения
если у(0)=1.
Решение: Положим, что у(х) является решением данного дифференциального уравнения при указанных начальных условиях. Если у(х) допускает разложение в ряд Маклорена, то имеем:
(1)
Свободный член
разложения (1), то есть у(0), дан по условию.
Чтобы найти значения
нужно данное уравнение последовательно
дифференцировать по переменной х и
затем вычислять значения производных
при х = 0.
Значение
получаем, подставив начальное условие
в дифференциальное уравнение
Подставив найденные значения производных при х = 0 в (1), получим разложение искомого частного решения заданного уравнения:
Ответ: 