6. Внешняя спецификация программы

Во внешней спецификации указывается, как происходит диалог пользователя с программой. Также необходимо показать, как программа будет реагировать на ввод недопустимых исходных данных.

В одинарных угловых скобках <> размещены исходные данные, вводимые пользователем. В двойных угловых скобках <<>> приведены данные, выводимые на экран программой. Звездочка и двойные фигурные скобки обозначают возможность повторного выполнения действий. Одинарные фигурные скобки и условие показывают возможность выбора одной из двух альтернатив.

Ниже приведена внешняя спецификация для программы построения графиков функций.

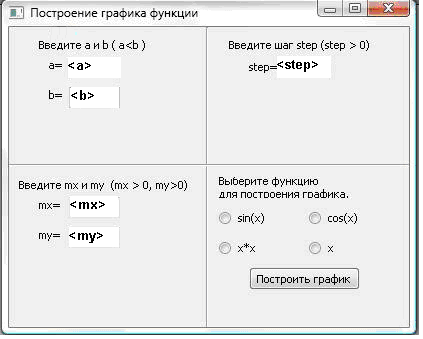
Значения исходных данных вводятся в соответствующие поля.

При недопустимых исходных данных происходит вывод сообщения об ошибке. Ниже перечислены возможные варианты сообщений, которые будут выводиться в различных случаях.

п ри a≥b или a ₵ R или b ₵ R

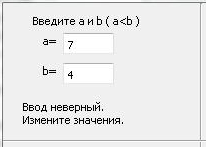
до a <b и a Є R и b Є R

п ри step≤0 или step ₵ R

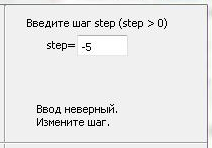
до step>0 и step Є R

п ри mx≤0 или my≤0 или mx ₵ R или my ₵ R

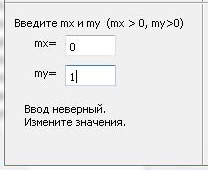
до mx>0 и mx Є R и my>0 и my Є R

Для выбора функции из заданного набора используются кнопки

(RadioButton):

После того как выбраны верные значения всех параметров и одна функция из заданного набора, окно выбора параметров принимает вид:

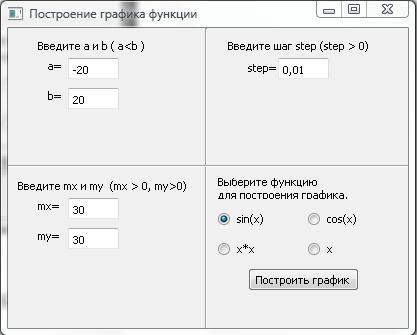
Для начала построения графика необходимо нажать на кнопку . После этого на экране изображается график функции:

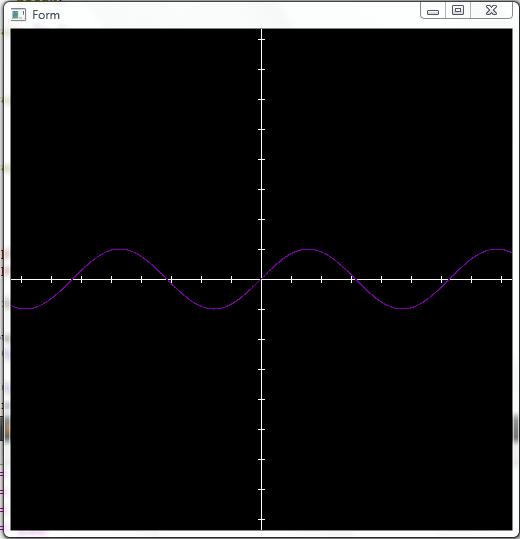
7. Метод решения задачи

В методе решения задачи записываются формулы, которые будут применяться для получения результата. В случае, если алгоритм не содержит вычислений по формулам, возможно словесное описание метода решения задачи.

Для программы построения графиков функций метод решения можно описать следующим образом.

Вначале строятся оси координат и на осях откладываются единичные отрезки. При этом используются следующие переменные:

• nx, ny – число единичных отрезков, откладываемых от 0 до конца отрезка соответствующей координатной оси, размещаемой на экране;

• mx, my – масштабные коэффициенты по осям Ox и Oy ;

• pix_size=501– максимальные координаты точки по осям Ox и Oy (т.е. максимальный размер окна);

• n – номер функции (выбирается одна функция из данного списка );

• a, b – границы отрезка;

• step – расстояние между точками графика (шаг);

• x, y – математические координаты точки экрана.

К оличество единичных отрезков вычисляется по формулам:

При построении единичных отрезков используются следующие формулы.

Д ля оси Ox:

для x=-nx; nx шаг 1.

Для оси Oy те же формулы используются для y=-ny; ny шаг 1.

При построении графика используются приведенные выше формулы для xm, ym и вычисляются значения y=f(x) для x=a; b с шагом step.

8. Описание алгоритма

В данном разделе необходимо привести полное описание алгоритма решения поставленной задачи. Описание должно отражать метод пошаговой детализации, используемый при разработке алгоритма: сначала описывается алгоритм главной программы, затем из неё выделяются подпрограммы, после чего описывается алгоритм каждой подпрограммы и т.д. Описание алгоритма каждой подпрограммы включает описание исходных данных, результата, связи и текст алгоритма на псевдокоде с использованием базовых структур: простая последовательность действий, условная конструкция и цикл. Логические условия и действия, выполняемые в алгоритме, описываются в словесной форме.