7.6. Методы расчета конструкций
Метод расчета фундаментов зависит от формы подошвы и относительной гибкости фундамента. Если конструкция имеет удлиненную прямоугольную опорную площадь, причем любая полоса шириной 1 м, выделенная в поперечном направлении из конструкции, работает в одинаковых условиях со всякой другой подобной полосой, т.е. имеет одинаковую жесткость и одинаковое распределение внешней нагрузки (рис.35), то расчет этой полосы проводится в условиях плоской задачи. При этом длина опорной площади должна быть по крайней мере в 3 раза больше ширины. В условиях плоской задачи рассчитываются главным образом фундаменты гидротехнических сооружений.
Рис.35. Схема выделения полосы из конструкции для расчета в условиях плоской задачи
Круглые и кольцевые фундаментные плиты рассчитываются на основе решения осесимметричной задачи. К ним относятся фундаменты доменных печей, фундаменты типа конусных оболочек и т.п.
Ленточные фундаменты под колонны рассчитываются как балки в условиях пространственной задачи. Фундаменты из перекрестных лент в силу сложности их конструкции рассчитываются по гипотезе Винклера. Плоские прямоугольные фундаменты под отдельные колонны рассчитываются как прямоугольные плиты в условиях пространственной задачи. При значительной их жесткости допустимо проводить расчет обычным способом, исходя из гипотезы о равномерном распределении реактивных давлений. Сплошные фундаментные плиты под ряды колонн или под стены (в том числе каркасных зданий), под полы промышленных зданий и т.п. рассчитываются с помощью ЭВМ как плиты большой протяженности.
Методы расчета конструкций на упругом основании (кроме плит большой протяженности) разделяются на две группы:
методы, в которых на основе условий равновесия и условия полного примыкания подошвы балки или плиты к грунту составляются одна или две системы линейных уравнений с несколькими неизвестными; решение этих систем позволяет определить эпюру реактивных давлений, а затем уже и эпюры изгибающих моментов, поперечных сил и прогибов (осадок);
методы, основанные на использовании готовых таблиц всех этих расчетных величин; такие таблицы составлены для большинства типов конструкций при различной их относительной гибкости, характере и размещении нагрузок и значительно сокращают время и труд расчетчика.
И в том, и в другом случае трением между подошвой фундамента и основанием принято пренебрегать (в запас прочности).
Основными методами, требующими решения систем уравнений, являются следующие:
1. Метод Б. Н. Жемочкина. Этот метод применим для расчета как балок в условиях пространственной задачи, так и полос в условиях плоской задачи. Здесь вся опорная площадь фундамента разбивается на ряд участков, причем в пределах каждого участка реакции грунта для упрощения считаются равномерно распределенными (рис.36).
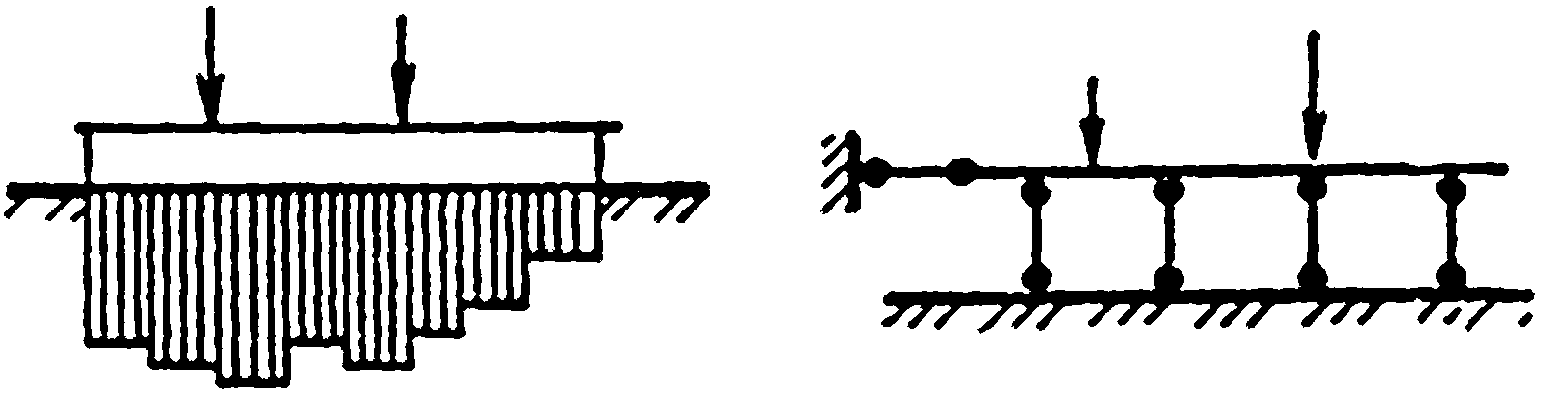
Рис.36. К расчету балки или полосы по методу Б.Н.Жемочкина
Между балкой (полосой) и основанием в середине каждого участка помещается абсолютно жесткий стержень (на рис.36 для ясности число стержней сокращено). Горизонтальный стержень поставлен для того, чтобы сделать систему неизменяемой: он никакой роли в расчете не играет. Постановкой вертикальных стержней-связей ставится условие, что вертикальные перемещения балки и основания в местах этих стержней одинаковы.
Неизвестными в расчете являются силы Fi в стержнях, осадка si и угол поворота tg αi в каком-либо сечении балки, принимаемом за начальное. Эти неизвестные определяются исходя из условия равенства прогибов балки и осадки грунта в точках, где поставлены стержни. К полученным контактным уравнениям прибавляются два уравнения, вытекающие из условия равновесия.
Аналогичный метод тем же автором предложен для расчета круглых и кольцевых плит.
Метод Б. Н. Жемочкина особенно удобен при переменном сечении балки или сложной форме подошвы. Он обобщается на случай, когда основание представляет собой сжимаемый слой конечной толщины. Метод неприменим для расчета прямоугольных плит в строгой постановке, когда в каждой точке плиты определяются два момента, изгибающих плиту соответственно в продольном и поперечном направлениях. Его нельзя также использовать для расчета длинных ленточных фундаментов под ряд колонн.
2. Метод М. И. Горбунова-Посадова. Этот метод охватывает все основные типы конструкций на упругом основании. Эпюра реактивных давлений здесь определяется в виде многочлена 10-й степени. При симметрично нагруженной полосе многочлен для плоской задачи имеет вид:
р (х) = а0 + а2х2 + а4х4 + а6х6 + а8х8 + а10х10, (136)
где х=х`/l – приведенное расстояние от середины полосы до данной точки (где х` - действительное расстояние; l – полудлина полосы).
При нессиметричной нагрузке к многочлену (136) добавляется многочлен с нечетными степенями х 9-й степени. Расчет при симметричной нагрузке приводит к решению системы из шести уравнений относительно неизвестных а2i, а в общем случае – двух систем с шестью и пятью неизвестными. Эти системы получаются путем приравнивания перемещений поверхности грунта ω (х) от давлений р (х) прогибам полосы от тех же давлений. Давления р (х) для полосы являются реактивными давлениями, направленными снизу вверх. И перемещения поверхности, и прогибы выражаются так же через степенные ряды, коэффициенты которых линейно зависят от коэффициентов а2i и а2i+1. Приравнивание коэффициентов при одинаковых степенях в уравнении перемещений и прогибов и дает нужные системы уравнений. При пространственной задаче метод аналогичен, но в решении участвуют уже двойные степенные ряды.