7. Расчет плитных и ленточных фундаментов под колонны

7.1. Общие положения

Расчет ленточных и плитных фундаментов, работающих на изгиб, проводится с учетом совместной работы конструкции и грунтового основания согласно теории конструкций на упругом основании. В этом случае предположение о линейном распределении реактивных давлений уже не может рассматриваться как достаточно точное, так как изгиб конструкции изменяет распределение этих давлений и, следовательно, отражается и на усилиях в балках и плитах. Линейное распределение давлений используется лишь для предварительного определения сечений конструкций.

7.2. Предварительное назначение размеров сечений

Предварительное назначение размеров сечений рассмотрим на примере ленточного фундамента под колонны, исходя из схемы линейного распределения реактивных давлений. Изгибающие моменты в каждом сечении ленты определяются по формуле

М = М_l – ΣP_il_i + ΣM_i, (131)

где М_l – момент в данном сечении от площади эпюры реактивных давлений, расположенной левее данного сечения; ΣP_il_i - сумма моментов для данного сечения от нагрузок, передаваемых колоннами, расположенными левее сечения (здесь P_i – нагрузка от колонны i; l_i – расстояние от колонны до сечения); ΣМ_i - сумма внешних моментов, передаваемых колоннами, расположенными левее данного сечения.

За положительное направление моментов принимается направление по часовой стрелке.

Таким образом, изгибающие моменты определяются простейшим способом по схеме статически определяемой балки. Не рекомендуется пользоваться расчетом статически неопределимой неразрезной балки, нагруженной трапецеидальной эпюрой давлений, при котором опорные реакции оказываются отличными от расчетных нагрузок, передаваемых на балку колоннами; кроме того, такой расчет сложнее. Использование схемы неразрезной балки оправдано лишь в том случае, если жесткость верхнего строения очень велика и не позволяет смещаться опорным точкам колонн нелинейно относительно друг друга. В этом случае учитывается перераспределение внешней нагрузки по колоннам, исходя из учета жесткости верхнего строения.

7.3. Расчет фундаментных балок и плит как конструкций на упругом основании

Для учета влияния изгиба на распределение реактивных давлений используется одно из двух предположений.

1. Основание работает согласно гипотезе коэффициента постели (Винклера). Эта гипотеза предполагает, что осадка какой-либо точки (элемента) поверхности основания s пропорциональна давлению р, приложенному в той же точке, т.е. р=k_ss. Коэффициент k_s, Па/м, называется коэффициентом постели. Осадка данной точки (элемента) зависит только от давления, приложенного в этой точке, и не зависит от давлений, действующих по соседству (рис.33, а).

2. Основание работает как среда, к которой применимы формулы теории упругости, связывающие напряжения и осадки. Грунт принимается за однородное упругое тело, бесконечно простирающееся вниз и в стороны и ограниченное сверху плоскостью (упругое полупространство), а соответствующее предположение называется гипотезой упругого полупространства. Поверхность упругого полупространства деформируется не только непосредственно под нагрузкой, но и по соседству с ней (рис.33, б). Деформационные свойства грунта характеризуются в основном модулем деформации Е₀, МПа.

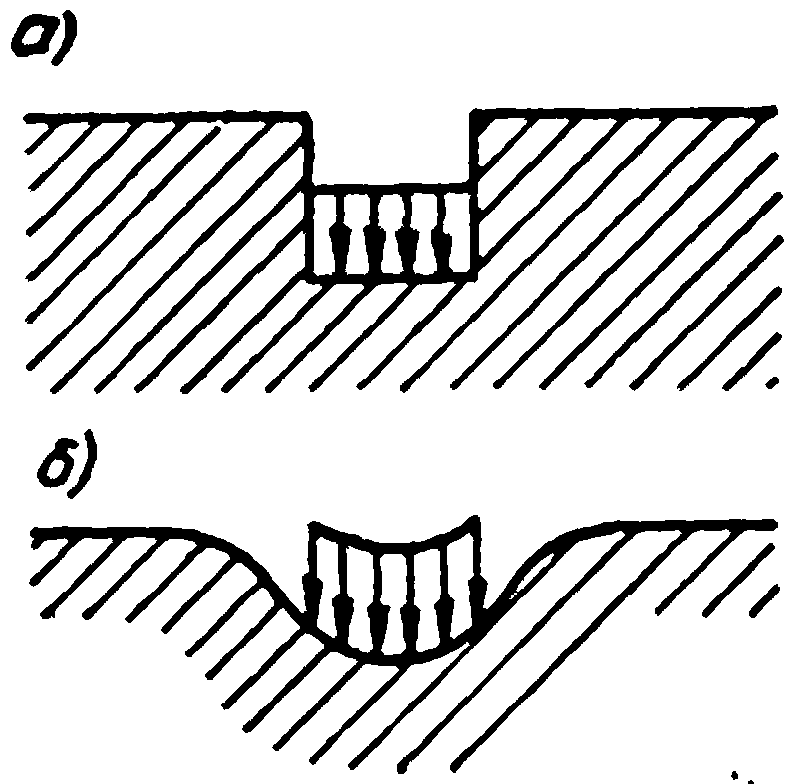
Рис.33. Перемещение поверхности основания под нагрузкой

а – по гипотезе Винклера; б – по гипотезе упругого полупространства

Согласно гипотезе коэффициента постели, грунт лишен распределительной способности, т.е. деформации соседних с нагрузкой элементов поверхности грунта отсутствуют. Коэффициент постели для данного типа основания предполагается величиной, не зависящей от площади фундамента (в действительности – зависит).

В гипотезе упругого полупространства распределительная способность преувеличена. Модуль деформации является характеристикой, представляющей одновременно как упругие, так и остаточные деформации. При многократном приложении нагрузки остаточные деформации исчезают, модуль общей деформации Е₀ переходит в модуль упругости Е, значительно больший, чем Е₀. При ширине фундамента примерно от 70 см до 7 м значение модуля деформации меняется незначительно. При превышении ширины 7 м модуль деформации заметно возрастает.