2.2.3 Дифракция Фраунгофера от щели.
П
усть
на плоскопараллельную щель падает
плоская монохроматическая волна.
Поместим за щелью собирающую линзу, а
в фокальной плоскости линзы - экран (см.
рис.2.9). Когда световая волна достигает
отверстия щели, то каждая точка согласно
принципу Гюйгенса становится источником
сферических волн, распространяющихся
по всем направлениям.
Из
этого множества лучей выберем лучи,
идущие под углом φ
к волновому вектору. Пусть
составляет
целое число
,
например,
т.е.
рассматриваемая в выбранном направлении
волновая поверхность ОА состоит из 3-х
зон Френеля. Если
- число зон Ф., то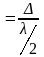 
.
При = 2m получим минимум интерференции, а при = 2m+1 - максимум интерференции, следовательно, условие максимума для дифракции от щели:
или
.
(2.7)
Условие
минимума:
(2.8)
(Для
вакуума
)
На рис.2.10 представлена интенсивность света в зависимости от - числа зон Френеля, наблюдаемых в данной точке экрана. Точка =0 принадлежит центру экрана (нормальной проекции центра щели на экран).
2.2.4. Дифракционная решетка
Д
ифракционной
решеткой называется
совокупность большого числа одинаковых,
отстоящих друг от друга на одно и то же
расстояние щелей (рис.2.11). Расположим
параллельно решетке собирательную
линзу, в фокальной плоскости которой
поставим экран. Плоская монохроматическая
световая волна падает на решетку
нормально.
Из множества вторичных световых волн выберем лучи, идущие под углом φ к волновому вектору падающей волны. В последствии мы будем изменять угол φ, чтобы учесть всевозможные направления. Множество лучей, идущих под углом φ, в свою очередь представим как совокупность пар соответственных лучей, испускаемых точками щелей, отстоящими друг от друга на одинаковые расстояния, равные d
(d = a + b) - постоянной решетки.
Если оптическая разность хода между, парой соседних соответственных лучей равна:
= mλ,
то волны усиливают друг друга, т.е. выполняется условие максимума интерференции. Следовательно, направление на главные максимумы для дифракционной решетки имеет вид:
dsinφ = mλ , (2.9)
где
m
= 0,
1,
2,
3,
...
Однако,
это выражение дает не полную картину
распределения интенсивности по углам
φ. Обратим внимание на то, что соответственные
лучи сдвинуты по отношению друг к другу
на некоторую фазу
.
Т.е. фактически происходит интерференция
N
лучей одинаковой амплитуды (где N - число
щелей в решетке), сдвинутых по фазе на
.
Строгая теория учитывает этот факт (см.
И.В.Савельев. Курс общей физики. Т.2. 1988.
с.407 - 415).
У
чет
многолучевой интерференции показывает,
что кроме главных максимумов есть
добавочные максимумы, расположенные в
промежутках между первыми. Число m
дает порядок главного максимума. Максимум
нулевого порядка только один, максимумов
1-го, 2-го и т.д. порядка - по два. На рис.2.12
приведена качественная картина
распределения интенсивности света по
поверхности экрана.
(Объяснить самостоятельно причину появления дифракционных спектров при освещении решетки белым светом)
Дифракционные решетки успешно применяют в оптическом приборостроении (например, в спектрографах вместо стеклянных призм, благодаря чему достигается более четкое разделение составляющих спектра), они могут быть использованы для определения длины волны неизвестного ранее источника света.
Особо важное в науке и лабораторной практике значение имеет дифракция коротковолнового электромагнитного излучения (рентгеновских лучей) на пространственной дифракционной решетке, образованной молекулами кристаллов.