4.8. Электрон в «потенциальной яме» Квантование энергии
Уравнение Шредингера позволяет решать практические задачи и находить состояния движения частиц в различных внешних полях.
Э
лектрические
свойства металлов объясняются наличием
в них свободных электронов. Результирующая
сила, действующая на электрон со стороны
ионов и всех остальных электронов, в
среднем равна нулю. Следовательно,
потенциальная энергия ЕП
электрона внутри металла постоянна и
ее можно выбрать за начало отсчета и
считать равной 0.
На границах металла расположен двойной электрический слой, для преодоления которого нужно затратить работу выхода АВЫХ. Поэтому потенциальная энергия электрона вне металла ЕП= АВЫХ > 0.
Направим ось х перпендикулярно к грани бруска металла длиной l . Потенциальная энергия Еп показана на рис.4.2.
Уравнение Шредингера в рассматриваемом случае имеет вид:
,
(т.к Еп=0) (4.10)
Решением этого однородного дифференциального уравнения 2-го порядка является функция:
(4.11)
где
k
=
,
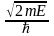а С1
и С2
- постоянные, определяемые из граничных
условий и условия нормировки.
Пока
кинетическая энергия электрона мала
по сравнению с высотой стенок «потенциальной
ямы»
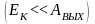электрон не имеет возможность выйти за
пределы потенциальной ямы, поэтому
граничные условия состоят в следующем:
(4.12)
(4.13)
Условие (4.12) после подстановки в (4.11) дает С2 = 0, а условие (4.13) приводит к выражению sin kl = 0, из которого следует:
kl = nπ, где n =1, 2, 3… (4.14)
П
ри
этом учтено, что С1
0,
т.к. электрон находится внутри ямы –
это достоверно и что k
0
в силу того, что электрон движется.
Запишем выражение (4.14) в развернутом
виде:
.
Откуда следует, что энергия электрона может иметь только дискретные значения Е(n):
(4.15)
На рис.4.3 дана схема разрешенных энергетических уравнений. Числа n называются «квантовыми» числами.
Заметим, что квантование энергии частиц впервые ввел Н.Бор ещё до создания квантовой механики.
4.9.Теория атома водорода по Бору
4.9.1.Модель атома Резерфорда
Первым научным представлением о строении атома была томсоновская модель: «размазанный» положительный заряд, в котором плавают электроны.
В 1911 году английский физик Резерфорд на основании своих исследований предложил планетарную модель атома:
Вокруг положительного ядра, имеющего заряд Z∙e (где Z – порядковый номер элемента в системе Менделеева, e – элементарный заряд), размер которого 10-15 – 10-14 м и массу, практически равную массе атома, в области с линейными размерами ~10-10 м по замкнутым орбитам движутся электроны, образуя электронную оболочку атома. Т.к. атомы нейтральны, то заряд ядра равен суммарному заряду электронов, т.е. вокруг ядра вращается Z электронов.
На основании второго закона Ньютона для электрона, движущегося по окружности под действием кулоновской силы:
.
Здесь r и v - неизвестные величины. Существует бесчисленное множество значений радиуса и соответствующих ему значений скорости (а значит и энергии Е), удовлетворяющих этому уравнению. Поэтому величины r и v (следовательно и Е) могут меняться непрерывно, т.е может испускаться любая энергия. Тогда спектры атомов должны быть сплошными. (Однако, в действительности, атомы имеют линейчатые спектры.) Кроме того, по законам электродинамики движущийся вокруг ядра с центростремительным ускорением электрон излучает электромагнитные волны и, непрерывно теряя энергию, должен «упасть» на ядро. Атом по Резерфорду получился неустойчивой системой.