
Регрессионные модели с переменной структурой (фиктивные переменные).
Регрессионная модель с переменной структурой — это такая модель, которая учитывает неоднородность количественной зависимой переменной с помощью качественного фактора (фиктивной переменной).
Термин “фиктивные переменные” используется как противоположность “значащим” переменным, показывающим уровень количественного показателя, принимающего значения из непрерывного интервала. Как правило, фиктивная переменная — это переменная, отражающая качественную характеристику. Это могут быть разного рода атрибутивные признаки, такие, например, как профессия, пол, образование, климатические условия, принадлежность к определенному региону. Чтобы ввести такие переменные в регрессионную модель, им должны быть присвоены те или иные цифровые метки, т. е. качественные переменные преобразованы в количественные. Такого вида сконструированные переменные в эконометрике принято называть фиктивными переменными.
Качественные признаки могут существенно влиять на структуру линейных связей между переменными и приводить к скачкообразному изменению параметров регрессионной модели. В этом случае говорят об исследовании регрессионных моделей с переменной структурой или построении регрессионных моделей по неоднородным данным.
Например, нам надо изучить зависимость размера заработной платы Y работников не только от количественных факторов Х1, X1..., Хn, но и от качественного признака Z1 (например, фактора «пол работника»).
В принципе можно было получить оценки регрессионной модели (1)
![]()
для каждого уровня качественного признака (т. е. выборочное уравнение регрессии отдельно для работников-мужчин и отдельно — для женщин), а затем изучать различия между ними. Но есть и другой подход, позволяющий оценивать влияние значений количественных переменных и уровней качественных признаков с помощью одного уравнения регрессии. Этот подход связан с введением так называемых фиктивных (манекенных) переменных.
В качестве фиктивных переменных обычно используются дихотомические {бинарные, булевы) переменные, которые принимают всего два значения: «О» или «1» (например, значение такой переменной Z1 по фактору «пол»: Z1= О для работников-женщин
и Z1=1 — для мужчин).
В
этом случае первоначальная регрессионная
модель заработной платы изменится и
примет вид:
 (2)
(2)
Таким
образом, принимая модель (5.2), мы считаем,
что средняя заработная плата у мужчин
на
 • 1=
выше, чем у женщин, при неизменных
значениях других параметров модели. А
проверяя гипотезу H0:
= О, мы можем установить существенность
влияния фактора «пол» на размер заработной
платы работника.
• 1=
выше, чем у женщин, при неизменных
значениях других параметров модели. А
проверяя гипотезу H0:
= О, мы можем установить существенность
влияния фактора «пол» на размер заработной
платы работника.
Следует отметить, что в принципе качественное различие можно формализовать с помощью любой переменной, принимающей два разных значения, не обязательно «О» или «1». Однако в эконометрической практике почти всегда используютсяфиктивные переменные типа «0—1», так как при этом интерпретацияполученных результатов выглядит наиболее просто.
Рассмотрим методы анализа качественных переменных на конкретном примере.
Задача 2
По условной области была взята выборка, состоящая из 18 предприятий, каждое предприятие характеризуется двумя качественными переменными:
— состояние приватизации;
— состояние рентабельности. Переменная А имеет два класса:
(A1) — приватизированные и (А2) — неприватизированные.
Переменная В тоже имеет два класса:
(B1) — рентабельные и (В2) — нерентабельные.
Количество предприятий fij, обладающих свойствами AiBj, представлено в таблице сопряженности (табл. 1)
Таблица 1
Перекрестные данные двух качественных переменных
Состояние приватизации (Аi) i = l, m |
Состояние рентабельности (B j) j = l, k |
Всего |
Средние значения
|
|
рентабельные (В1) |
нерентабельные (B2) |
|||
Приватизированные (А1) |
f11 = 8 |
f12 = 4 |
f10 = =f11+f12=12 |
|
Неприватизированные (А2) |
f21 = 2 |
f22 = 4 |
f20= f21+f22=6 |
|
Всего |
f01=f11+f21=10 |
f02=f12 + f22 = 8 |
f00=f10+f20=f01+f02=18 |
|
Средние значения
|
|
|
|
|
Анализ качественных переменных основывается на двух простых утверждениях:
изменения частот объектов можно объяснить отдельным влиянием переменных, а также их взаимовлиянием;
если доля приватизированных предприятий среди прибыльных равна доле приватизированных предприятий среди убыточных предприятий, то приватизация не оказывает влияния на рентабельность.
Необходимо решить следующие задачи.
Задача 1.
Найти долю приватизированных предприятий среди рентабельных и долю приватизированных среди нерентабельных предприятий.
Доля приватизированных предприятий среди рентабельных составляет:
d1=

Доля приватизированных среди нерентабельных предприятий составляет:
d2=

Задача 2.
Найти вероятность рентабельности и нерентабельности приватизированного предприятия.
Вероятность того, что приватизированное предприятие будет рентабельным, составляет:
p1=
Вероятность того, что приватизированное предприятие будет нерентабельным, составляет:
p2= =0,384615
=0,384615
Задача 3.
Определить, в каком случае приватизация оказывает положительное влияние на рентабельность.
Если вероятность рентабельности приватизированного предприятия больше вероятности его нерентабельности, то приватизация оказывает положительное влияние на рентабельность.
Р1 > Р2 или d, > d2 или f11/f01 > f12/f02;
K= P1/P2 = 1,6.
Вывод. Если предприятие приватизировано, то вероятность его рентабельности в 1,6 раза больше вероятности нерентабельности. Приватизация оказывает положительное влияние на рентабельность.


 =6
=6 =3
=3
 Bj
Bj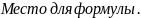
 =5
=5 =4
=4 =4,5
=4,5