1)Релятивистский импульс

Уравнения классической механики инвариантны по отношению к преобразованиям Галилея, по отношению же к преобразованиям Лоренца они оказываются неинвариантными. Из теории относительности следует, что уравнение динамики, инвариантное по отношению к преобразованиям Лоренца, имеет вид: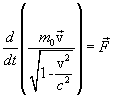 где  - инвариантная, т.е. одинаковая во всех системах отсчета величина называемая массой покоя частицы, v- скорость частицы,  - сила действующая на частицу. Сопоставим с классическим уравнением Мы приходим к выводу, что релятивистский импульс частицы равен 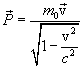Выражение, обеспечивающее инвариантность закона сохранения импульса, может быть получено, если вместо времени t подставить собственное время τ.

Тогда  .

Основное уравнение динамики движения релятивистской частицы имеет вид, схожий с основным уравнением движения классической динамики:  однако, при дифференцировании по времени правой части нужно учесть, что релятивистская масса не есть постоянная величина. Отметим, что классическая формулировка второго закона Ньютона  несправедлива даже с релятивистской массой. Найдём связь массы и энергии тела Для этого преобразуем уравнение (12.6):

Если дифференциалы величин равны, то сами величины могут различаться на постоянную величину:  . Значение этой константы можно найти из условия, что при , выражение для кинетической энергии должно стремиться к  Значение ее окажется равным  . Таким образом, получаем релятивистское выражение для кинетической энергии:  . Отметим, что классические выражения для кинетической энергии, как  неприменимы, даже если в них подставить релятивистские массы. Второе слагаемое в этом выражении имеет смысл энергии покоя, внутренней энергии тела, энергии связанной с самим фактом существования тела и наличием у него массы в неподвижном состоянии. Сумма кинетической энергии и энергии покоя называется полной энергией тела. Выражение для полной энергии можно получить из формулы (12.9).

2)Волновое уравнение - линейное дифференциальное уравнение в частных производных, описывающее малые колебания струны, колебательные процессы в сплошных средах и в электродинамике.      В общем случае волна, распространяющаяся в пространстве, описывается уравнением

(1)

где u = u(x,y,z,t) − возмущение в точке x,y,z в момент времени t, v − скорость распространения волны. Уравнение (1) инвариантно относительно замены v → -v.

Билет 14.

1)Полная релятивистская энергия.

Полная энергия и импульс частицы определяются соотношениями E = mc2γ,	(3)
p = γmv = vE/c2.

    Полная энергия и импульс частицы зависят от системы отсчетаю. Масса не меняется при переходе от одной инерциальной системы отсчета к другой. Она является лоренцевым инвариантом. Полная энергия импульс и масса связаны соотношением E² - p²c² = m²c⁴,где E, р и  m - полная энергия, импульс и масса частицы, с - скорость света в вакууме. Из соотношения (3) и (4) следует, что если энергия E и импульс p измеряются в двух различных системах движущихся друг относительно друга со скоростью v, то энергия  и импульс   будут иметь в этих системах различные значения. Однако величина E² - p²c², которая называется релятивистский инвариант, будет в этих системах одинаковой.      Полная и кинетическая энергия связаны между собой соотношением Е =  T + Е₀ = Т + mc², Т = Е - mc²,  где T - кинетическая энергия частицы, Е₀ - энергия покоя частицы. При изменении скорости движения изменяется релятивистский импульс и полная энергия тела. Их изменения взаимосвязаны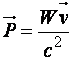 в скалярной форме

;             ;               . 

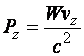При переходе от одной инерциальной системы отсчета к другой изменяется скорость движения, а следовательно, импульс и энергия. Несложно показать, что выражение является инвариантом относительно преобразований Лоренца и не зависит от выбора системы отсчета. Следовательно, .

2 )Скорость распространения упругих волн (V) — скорость распространения фазы упругого возмущения в разл.упругих средах. Скорость волны определяется скоростью распространения колебаний от одной точки среды к другой: Так как то, Скорость распространения волн тем меньше, чем инертнее среда, т.е. чем больше ее плотность. С другой стороны, она имеет большее значение в более упругой среде, чем в менее упругой. Скорость продольных волн определяется по формуле: , а поперечной: , где ρ- плотность среды, E - модуль Юнга, G - модуль сдвига. Так как для большинства твердых тел E>G то скорость продольных волн больше скорости поперечных.

Билет 15.