2)Физический маятник.

 

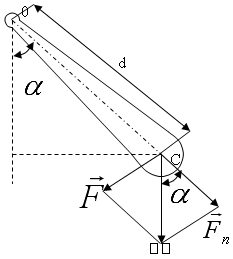
Физическим маятником называется твердое тело, колеблющееся относительно неподвижной горизонтальной оси (оси подвеса), не проходящей через центр тяжести. При небольших углах отклонения (α-мал) физический маятник совершает гармонические колебания. Сила, возвращающая маятник в положение равновесия, представляет собой составляющую силы тяжести, приложенную в точке С:

F=mg·sinα

Момент этой силы относительно оси O равен:

M=-Fl=-mgd·sinα,

где l=d·sinα - плечо силы F относительно оси O, знак минус соответствует тому, что момент M стремится вернуть маятник в положение равновесия, аналогично квазиупругой силе.

В соответствии с уравнением динамики вращательного движения:

M=Iε,

где ε=d²α/dt² - угловое ускорение, I - момент инерции маятника относительно оси О. Получаем:

I·d²α/dt²=-mgd·sinα (9)

Ограничившись малыми колебаниями (sinα~α), после преобразований получаем уравнение (9) в виде:

(d²α/dt²) + (mgdα/I)=0 (10)

Сравнив выражения (5) и (10) мы видим их математическую аналогию, что позволяет записать выражения для циклической частоты и периода колебаний физического маятника:

ω₀=√(mgd/I) (11)

T₀=2π/ω₀=2π√(I/mgd), (12)

где d - расстояние от центра тяжести до оси вращения.

Билет 4.

1)Движение центра масс твердого тела

Центр масс твёрдого тела – геометрическая точка,, положение которой характеризует распределение масс в теле или механической системе. Координаты Ц. и. определяются формулами :

.

Для тела при непрерывном распределении масс:

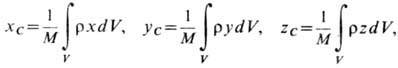,где m_k - массы материальных точек, образующих систему; x_k, y_k, z_k- координаты этих точек; М =Sm_k- масса системы; r( х, у, z) - плотность; V-объём.

Для системы тел , где   — радиус-вектор центра масс,   — радиус-вектор i-й точки системы,   — масса i-й точки.

Для случая непрерывного распределения масс: где   — суммарная масса системы,   — объём,   — плотность. Центр масс, таким образом, характеризует распределение массы по телу или системе частиц. Можно показать, что если система состоит не из материальных точек, а из протяжённых тел с массами  , то радиус-вектор центра масс такой системы   связан с радиус-векторами центров масс тел   соотношением^[2]:

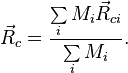Понятие Ц. и. отличается от понятия центра тяжести тем, что последнее имеет смысл только для твёрдого тела, находящегося в однородном поле тяжести; понятие же Ц. и. не связано ни с каким силовым полем и имеет смысл для любой механич. системы. Для твёрдого тела положения Ц. и. и центра тяжести совпадают. При движении механич. системы её Ц. и. движется так, как двигалась бы материальная точка, имеющая массу, равную массе системы, и находящаяся под действием всех внеш. сил, приложенных к системе. При  поступательном движении все точки твердого тела движутся так же, как и центр масс (по таким же траекториям), поэтому для описания поступательного движения достаточно записать и решить уравнение движения центра масс. При  поступательном движении все точки твердого тела движутся так же, как и центр масс (по таким же траекториям), поэтому для описания поступательного движения достаточно записать и решить уравнение движения центра масс.

2) Энергия гармонического осциллятора. Гармонический осциллятор (в классической механике) — система, которая при смещении из положения равновесия испытывает действие возвращающей силы F, пропорциональной смещению x (согласно закону Гука): , где k — коэффициент жёсткости системы.

Во время колебательных процессов происходит периодическое превращение потенциальной энергии системы в кинетическую. Например, отклонив математический маятник в сторону и, следовательно, подняв его на высоту h, ему сообщают потенциальную энергию  . Она полностью переходит в кинетическую энергию движения  , когда груз проходит положение равновесия и скорость его максимальна. При колебаниях пружинного маятника кинетическая энергия движения груза переходит в потенциальную энергию деформированной системы. Величина полной энергии колеблющейся системы в любой момент времени равна сумме ее кинетической и потенциальной энергии:

или

	.		(7.2)

Поскольку скорость – это первая производная от координаты по времени, то

.

Учитывая, что   и подставив выражения для   и  , получим:

.

То есть полная энергия системы, совершающей колебания, пропорциональна ее массе, квадрату амплитуды и квадрату собственной частоты. Так как силы, действующие на колеблющуюся частицу, являются консервативными, то ее механическая энергия остается постоянной. В процессе же колебаний происходит превращение кинетической энергии в потенциальную и обратно.

На рис. 7.3 приведен график зависимости потенциальной энергии от координаты частицы. С ростом x уменьшается кинетическая энергия и увеличивается потенциальная. Максимального значение потенциальная энергия достигает в поворотных точках  , при этом кинетическая энергия равна нулю. Среднее за период значение кинетической энергии равно среднему за период значению потенциальной энергии.

Билет 5.