Часть 2

Задание 1

Возможные значения дискретной случайной величины Х есть 0,1,2,3,4,5 Соответствующие вероятности равны р₀= ; р₁= . Найти вероятность р₂. Построить функцию распределения случайной величины Х, найти ее математическое ожидание и дисперсию.

Решение типового варианта.

Часть 1.

Задание 1. Сколько двухбуквенных комбинаций, не содержащих повторения букв, можно составить из 32 букв русского алфавита?

Решение. Искомые комбинации будут отличаться между собой или буквами, или их порядком. Поэтому искомое число равно числу размещений из 32 букв по 2, по формуле вычисления размещений имеем: двухбуквенные комбинации.

По данным «Словаря русского языка» из этих 992 комбинаций 114 выступают в качестве самостоятельных слов. Например, да, ад, еж, ус, он, як, яр, и т.д. Остальные 878 комбинаций бессодержательны с точки зрения русского языка.

Задание 2. Известно, что тексты, принадлежащие А. С. Пушкину, содержат 544777 словоупотреблений. Среди них 8771 раз употреблены различные формы слова «быть». Найдите вероятность того, что слово, выбранное наугад из произведений А. С. Пушкина окажется формой слова «быть».

Решение. Мы имеем: n=544777, n(A)=8771,

и по формуле вычисления вероятностей р(А)=n(A)/n=8771/544777=0,0161.

Задание 3(1). Группа туристов из пятнадцати юношей и пяти девушек выбирает по жребию хозяйственную команду в составе четырех человек. Какова вероятность того, что в составе этой команды окажутся два юноши и две девушки?

Решение. Испытание состоит в том, что из двадцати человек выбирают 4 человека. Так как выбор осуществляется по жребию, то все исходы испытания равновероятны и, кроме того, они несовместны. Число исходов испытания , так как выборка состоит из четырех элементов и порядок их расположения в выборке не учитывается. Пусть событие А состоит в том, что в составе выбранных окажутся два юноши и две девушки. Двух юношей из 15 можно выбрать способами и после каждого такого выбора двух девушек из 5 можно выбрать способами. По правилу произведения событию А благоприятствует исходов испытания. Искомая вероятность вычисляется по формуле

р(А)=т/n= .

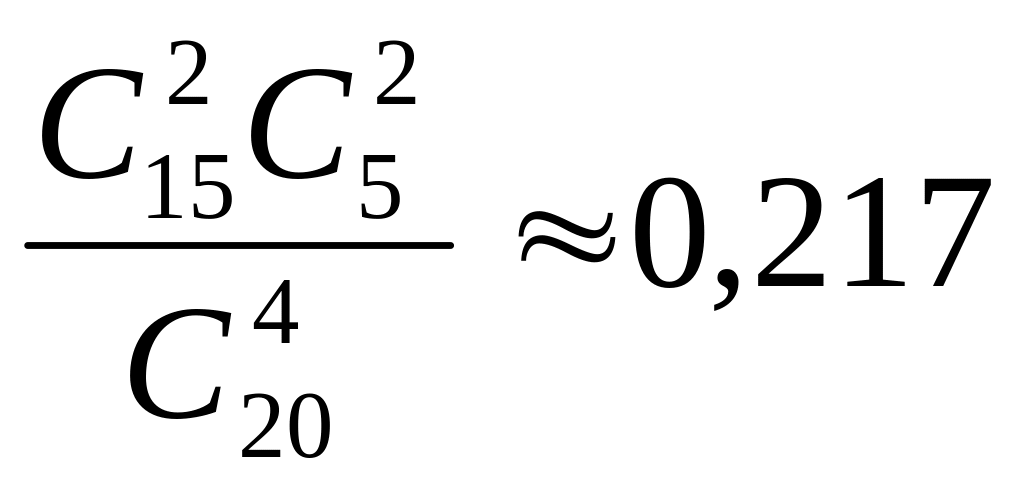Задание 3(2). На карточках написаны целые числа от 1 до 15 включительно. Наудачу извлекаются две карточки. Какова вероятность того, что сумма чисел, написанных на этих карточках, равна десяти.

Решение. Испытание состоит в том, что извлекают две карточки из 15 штук. Число исходов испытания . Событию А, состоящему в том, что сумма чисел, написанных на этих карточках, равна десяти, благоприятствует т=9 исходов (1+9, 2+8, 3+7, 4+6, 5+5, 6+4, 7+3, 8+2, 9+1). Таким образом, вероятность события А равна р(А)=т/п=9/ =0,09.

Задание 4.

В первом ящике 2 белых и 10 черных шаров; во втором ящике 8 белых и 4 черных шара. Из каждого ящика вынули по шару. Какова вероятность, что оба шара белые; один белый и один черный; хотя бы один белый?

Решение. В данном случае речь идет о совмещении событии А и В,

а) событие А – появление белого шара из первого ящика, событие В – появление белого шара из второго ящика. При этом А и В – независимые события. Имеем р(А)=2/12=1/6, р(В)=8/12=2/3. Применив теорему умножения вероятностей, находим

р(АВ)= р(А)∙р(В)=(1/6)∙(2/3)=1/9.

б) Пусть

событие А – появление белого шара из первого ящика;

событие В – появление белого шара из второго ящика;

событие С – появление черного шара из первого ящика (С= );

событие D – появление черного шара из второго ящика (D= ).

Тогда р(А)=2/12=1/6, р(В)=8/12=2/3, р(С)= р( )=1-1/6=5/6, р(D)= р( )=1-2/3=1/3.

Определим вероятность того, что шар, вынутый из первого ящика, белый, а из второго ящика – черный:

р(АD)= р(А)∙р(D)=(1/6)∙(1/3)=1/18.

Определим вероятность того, что шар, вынутый из первого ящика, черный, а из второго ящика – белый:

р(ВС)= р(В)∙р(С)=(2/3)∙(5/6)=10/18=5/9.

Определим теперь вероятность того, что шар, вынутый из одного ящика (безразлично из первого или второго), окажется белым, а шар, вынутый из другого ящика, - черным. Применяем теорему сложения вероятностей:

р= р(АD)+ р(ВС)=1/18+5/9=11/18.

в) р=р₁+р₂,

где

р₁ – вероятность того, что оба шара белые (см. случай а);

р₂ – вероятность того, что шар, вынутый из одного ящика (безразлично из первого или второго), окажется белым, а шар, вынутый из другого ящика, - черным (см. случай б).

Таким образом, вероятность того, что хотя бы один шар будет белым равна:

р=1/9+11/18=13/18.

Задание 6. Вероятность попадания стрелком в цель равна 0,7. Сделано 25 выстрелов. Определить наивероятнейшее число попаданий в цель.

Решение. Здесь п=25, р=0,7, q=0,3. Следовательно,

, т.е.

Так как т – целое число, то т=18.

Задание 7. Вероятность выхода первого станка из строя в течении рабочего дня равна 0,03, второго – 0,04. Какова вероятность того, что оба станка за 5 дней ни разу не выйдут из строя?

Решение. Так как

1-0,03=0,97 – вероятность того, что первый станок не выйдет из строя в течении дня, то по теореме умножения вероятностей 0,97⁵ – вероятность того, что первый станок не выйдет из строя в течении 5 дней.

1-0,04=0,96 – вероятность того, что второй станок не выйдет из строя в течении дня, то по теореме умножения вероятностей 0,96⁵ – вероятность того, что второй станок не выйдет из строя в течении 5 дней.

Тогда вероятность того, что оба станка за 5 дней ни разу не выйдут из строя будет равна р=0,85∙0,8=0,68.