Вопросы для самоконтроля

1. Какие методы используются для расчетов прочности железобетонных элементов по сечениям, нормальным к продольной оси при действии изгибающего момента и продольной оси?

2. Какие виды диаграмм деформирования и формы эпюр напряжений в бетоне сжатой зоны применяются в методах расчета прочности железобетонных элементов при действии изгибающего момента и продольной силы?

3. Какова область применения расчета прочности сечений при действии изгибающего момента и продольной силы по методу предельных усилий?

4. По какому критерию определяется расчетный случай разрушения нормальных сечений конструкций при действии изгибающего момента и продольной силы в методе предельных усилий?

5. Как изображается эмпирическая зависимость деформаций и напряжений в растянутой арматуре от относительной высоты сжатой зоны?

6. Что такое граничная относительная высота сжатой зоны сечения элемента и от чего она зависит?

7. Как записать основные расчетные формулы условий обеспечения прочности по нормальным сечениям для элементов прямоугольного профиля?

8. Какие условия определяют необходимость установки сжатой арматуры?

9. Какие условия обеспечивают прочность изгибаемых элементов прямоугольного профиля с двойной арматурой?

10. Какие условия обеспечивают прочность изгибаемых элементов таврового профиля?

11. Как определить положение границы сжатой зоны и расчетный случай для таврового профиля?

12. Какие установлены требования к вводимой в расчет прочности ширины свесов сжатой польки элементов таврового профиля?

Лекция 11. Прочность растянутых элементов

11.1. Центрально растянутые элементы.

Разрушение центрально растянутых элементов происходит после того, как в бетоне образуются сквозные трещины, он выключается из работы, а напряжения в арматуре для сечения, пронизанного трещиной, достигают предельных значений (физического или условного предела текучести). Условия равновесия для центрально растянутого элемента имеют вид:

(11.1)

или, записав равнодействующую F_st в напряжениях,

. (11.2)

Требуемую площадь растянутой арматуры из ф. (11.2) определяют:

, (11.3)

где f_yd – расчетное сопротивление растянутой арматуры.

Лекция 12. Прочность сечений, наклонных к продольной оси при действии поперечных сил

12.1. Формы разрушения наклонного сечения

В отличие от зоны «чистого изгиба», где действуют, главным образом, нормальные напряжения, в приопорной зоне железобетонная конструкция работает в ус­ловиях плоского напряженного состояния при совместном действии нормальных и касательных напряжений. Это приводит к тому, что в приопорной зоне конструкции в результате дей­ствия главных напряжений образуются наклонные или диагональные трещины, ориентированные под некоторым углом  к направлению продольной растянутой арматуры и разделяющие элемент на отдельные блоки, связанные между собой продольной арматурой в растянутой зоне, поперечной и (или) отогнутой арматурой, нетреснувшей частью бетона над вершиной наклонной трещины (рис. 12.1). В общем случае в расчетном наклонном сечении по линии А–В–С (рис. 12.1) действуют продольная F_cc1 и поперечная V_cd составляющие сил в бетоне над вершиной наклонной трещины; вертикальная V_ax и горизонтальная V_ay составляющие поперечной силы, возникающие за счет зацепления по берегам трещины; составляющая поперечной силы V_d, являющаяся результатом т.н. «нагельного эффекта» продольной арматуры, а также продольная составляющая F_t1, вызывающая ее растяжение; продольная и поперечная составляющие сил в поперечной арматуре (хомутах и отгибах) V_sw, пересекающих наклонную трещину.

Рис. 12.1. Схема внутренних усилий в наклонном сечении балки

Разрушение наклонного сечения может иметь одну из следую­щих форм, показанных рис. 12.2.

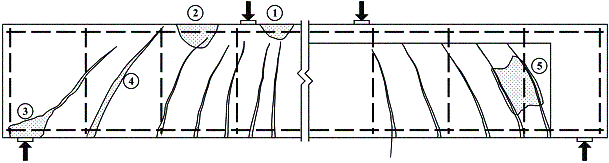
1 - изгибное разрушение в зоне действия максимальных изгибающих моментов; 2 - при срезе по сжатой зоне (форма I); 3 - то же по растянутой зоне (форма II); 4 - при срезе по диагональной трещине (форма III); 5 – по сжатой полосе между диагональными трещинами (форма IV).

Рис. 12.2. Формы разрушения балки

Форма I.

По наклонной трещине при достижении напряжениями в поперечной арматуре значений, равных пределу текучести от разрушения бетона над вершиной наклонной трещины (разрушение по сжатой зоне). В этом случае при развитии верхнего конца диагональной трещины сокращается высота сжатой зоны се­чения и деформации наиболее сжатой грани бетона по наклонному сечению достигают предельных значений (_cu).

Форма II.

По наклонной трещине при напряжениях в поперечной арматуре, равных пределу текучести в результате достижения предельных деформаций в растянутой продольной арматуре (разрушение по растянутой зоне). При нарушении анкеровки продольной арматуры или ко­гда раскрытие наклонной трещины в нижней части сечения приводит к развитию значительных де­формаций продольной арматуры при повороте образующихся частей балки относительно друг друга. В этом случае вдоль растянутой арматуры по направлению к опоре формируют­ся продольные трещины. Вместе с тем, раскалыва­ние является вторичным эффектом и связано с проскальзыванием арматуры относительно бетона.

Форма III.

По наклонной трещине при напряжениях в поперечной арматуре, равных пределу текучести, когда диагональная трещина доходит до верхней грани сечения и вызывает полное разделение бал­ки на две или несколько частей без разрушения бетона от сжатия. Диагональная трещина в этом случае раскрывается мгновенно. Такую форму разрушения называют разрушением при диагональ­ном растяжении.

Форма IV.

Разрушение по наклонному сечению, обусловленное раз­рушением при сжатии бетона полосы, заключенной между диагональными трещинами.

Разрушение по сжатой зоне (форма I) имеет место при сильной, хорошо заанкеренной про­дольной арматуре, а разрушение по растянутой зоне (форма II) — напротив - при ослабленной про­дольной арматуре в результате ее обрывов или ослаблении анкеровки продольной арматуры на опорах. Этот тип разрушения характерен для относительно коротких балок, армированных стерж­нями с низкими характеристиками сцепления. Третья форма разрушения достигается, когда меха­ническое сцепление и анкеровка арматуры достаточны. Разрушение по наклонной сжатой полосе (форма IV) наблюдается при большом коэффициенте поперечного армирования и тонкой стенке, например в элементах таврового и двутаврового сечения.

При расчете элементов по прочности наклонных сечений при совместном действии изги­бающих моментов, продольных и поперечных сил нормы допускают применять следующие уп­рощенные модели:

а) общая деформационная модель для наклонных сечений с диагональными трещинами (общий ме­тод), включающая уравнения равновесия и условия совместности относительных деформаций для железобетонного элемента в условиях плоского напряженно-деформированного состояния; транс­формированные диаграммы деформирования бетона для железобетонного элемента с диагональны­ми трещинами; диаграммы деформирования арматуры; зависимости, связывающие касательные на­пряжения и перемещения в сечении, проходящем вдоль диагональной (наклонной трещины);

б) стержневые модели, включающие сжатые и растянутые пояса, соединенные между собой сжа­тыми и растянутыми подкосами (модель «ферменной аналогии»), использующие уравнения равновесия внешних и внутренних сил в расчетном наклонном сечении;

в) модели наклонных сечений, включающие уравнения равновесия внешних и внутренних сил в расчетном наклонном сечении.