8.2. Критерий, определяющий расчетный случай разрушения

Метод расчета по предельным усилиям базируется на принципе пластического разрушения сечения, при котором достигаются предельные напряжения в растянутой арматуре и сжатом бетоне (принцип А.Ф. Лолейта).

На основании принципа А.Ф. Лолейта расчет нормального сечения по прочности производят, используя только лишь условия статического равновесия. Поэтому при расчете конструкции по методу предельных усилий необходимо прежде всего выяснить случай, по которому происходит разрушение нормального сечения.

Как было показано ранее, в третьей стадии напряженно-деформированного состояния разрушение сечения может происходить по двум случаям: по растянутой арматуре или по сжатому бетону. Деформации, а, следовательно, и напряжения, в растянутой арматуре зависят от высоты сжатой зоны сечения (х). Расчетная формула для определения относительных деформаций и напряжений в растянутой арматуре в зависимости от высоты сжатой зоны бетона, применяемая в методе предельных усилий, была получена базируясь на опытных данных. Обработкой результатов экспериментальных исследований установлено, что в предельном состоянии связь между приращениями деформаций арматуры De_s от внешних воздействий и относительной высоты сжатой зоны (при принятой прямоугольной эпюре распределения напряжений в сжатом бетоне) имеет в общем случае вид гиперболы (рис. 8.1).

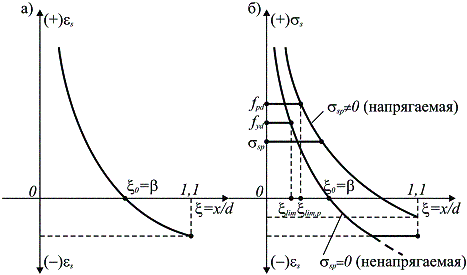
Рис. 8.1. Зависимость деформаций (а) и напряжений (б) в растянутой арматуре от относительной высоты сжатой зоны

Величина x₀, по существу, характеризует отклонение фактической эпюры напряжений в сжатой зоне сечения от принятой прямоугольной, то есть полноту эпюры напряжений в сжатом бетоне, обозначаемую далее b. Коэффициент полноты эпюры напряжений определяют по эмпирической формуле:

(8.1)

где a_с – коэффициент, принимаемый равным 0,85 для тяжелого бетона и 0,8 – для легкого бетона.

На рис. 8.1б показана зависимость напряжений в продольной арматуре s_s от относительной высоты сжатой зоны сечения x = x/d. Относительная высота сжатой зоны x_lim (относительная граничная высота сжатой зоны), при которой напряжения в растянутой арматуре достигают предела текучести, может быть определена из зависимости:

, (8.2)

где: для конструкций без предварительного напряжения, армированных мягкими сталями s_s,R = f_yd;

Таким образом, если

(8.3)

- растянутая арматура достигает предела текучести и, тем самым, реализуется принцип пластического разрушения нормального сечения;

(8.4)

- разрушение происходит по сжатому бетону и имеет место второй случай разрушения.

Следует отметить, что расчетная зависимость для определения x_lim является универсальной и может быть использована при расчете простых сечений при действии изгиба, внецентренного сжатия, внецентренного растяжения.

8.3. Расчетные уравнения

Проверку прочности нормальных сечений изгибаемых железобетонных элементов производят из условия:

, (8.6)

где: M_Sd –расчетный момент в рассматриваемом сечении, вызванный действием внешних нагрузок;

M_Rd –предельный момент, воспринимаемый сечением при заданных геометрических размерах, прочностных характеристиках бетона, количестве и размещении арматуры.

Прочность изгибаемых железобетонных элементов имеющих как минимум одну плоскость симметрии и изгибаемых в этой плоскости (рис.8.2) следует проверять из условия M_Sd £ M_Rd, где:

(8.7)

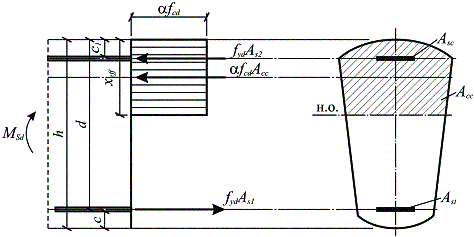
Рис. 8.2. Схема усилий и эпюра напряжений в сечении, нормальном к продольной оси изгибаемого железобетонного элемента

При этом высота условной сжатой зоны x_eff определяется из условия

(8.8)

При расчете элементов, имеющих полку в сжатой зоне сечения, следует ограничивать значение ее расчетной ширины b_eff из условия, что размер свеса полки в каждую сторону от ребра должен быть не более 1/6 пролета элемента и не более:

- при наличии поперечных ребер или при h'_f ³ 0,1h ¾ половины расстояния в свету между продольными ребрами;

- при отсутствии поперечных ребер или при расстоянии между ними большем, чем расстояние между продольными ребрами, и при h'_f < 0,1h равным 6h'_f .

- при консольных свесах полки и условии, что:

h'_f ³ 0,1h равным 6h'_f ;

0,05h £ h'_f £ 0,1 равным 3h'_f ;

h'_f < 0,05h - свесы не учитываются.

Расчет железобетонных изгибаемых элементов прямоугольного профиля (сечением b_w×h) следует производить из условия M_Sd £ M_Rd, где:

(8.9)

(8.10)

При этом высоту условной сжатой зоны x_eff определяют из условия

(8.11)

(8.12)

Расчет железобетонных изгибаемых элементов таврового и двутаврового сечений, имеющих полку в сжатой зоне сечения, следует производить следующим образом:

- если граница сжатой зоны проходит в пределах высоты полки (рис. 8.3а), т.е. соблюдается условие:

(8.13)

расчет производится как для прямоугольного сечения шириной, равной ширине полки b_f^/, по формуле:

(8.14)

Рис. 8.3. Положение границы условной сжатой зоны в сечении изгибаемого железобетонного элемента таврового сечения

а) в полке; б) в ребре

- если граница сжатой зоны проходит в ребре (рис. 8.3б), т.е. условие не соблюдается, расчет производится из условия M_Sd £ M_Rd, где:

(8.15)

При этом высоту сжатой зоны x_eff следует определять по формуле

(8.16)

Формулы действительны при x_eff≤ξ_lim·d, Для элементов выполненных из бетона классов С25/30 и ниже с арматурой классов S240, S400 и S500 при x_eff>ξ_lim·d допускается производить расчет из указанного условия принимая x_eff=ξ_lim·d.

При расчете внецентренно сжатых элементов следует различать два случая:

— случай большого эксцентриситета, когда x_eff /d £ x_lim (рис. 8.4);

— случай малого эксцентриситета, когда x_eff /d > x_lim (рис. 8.5).

Рис. 8.4. Схема усилий и эпюра напряжений в сечении, нормальном

к продольной оси внецентренно сжатого железобетонного элемента

(случай большого эксцентриситета)

Расчет внецентренно сжатых железобетонных элементов по прочности сечений, нормальных к продольной оси, для случая большого эксцентриситета (при x_eff /d £ x_lim) следует производить как для изгибаемых элементов (см. рис. 8.4), принимая

(8.17)

а высоту сжатой зоны определять из условия равновесия

_. (8.18)

Рис. 8.5. Схема усилий и эпюра напряжений в сечении, нормальном

к продольной оси внецентренно сжатого железобетонного элемента

(случай малого эксцентриситета)

При x_eff > x_lim×d расчет допускается производить из того же условия (как для изгибаемых элементов), но при этом высота сжатой зоны для элементов из бетона классов по прочности С²⁵/₃₀ и ниже должна определяться из условия

, (8.19)

где

(8.20)

Для элементов из бетона классов по прочности выше С²⁵/₃₀ при x_eff > x_lim×d расчет следует производить по деформационной расчётной модели.

В случае, когда расчетная продольная сила N_Sd не превышает 0,08N_cd (где N_cd = f_cd×A_c), допускается производить расчет внецентренно сжатых элементов по прочности как изгибаемых элементов, без учета продольной силы.