Физические измерения и обработка результатов

Введение

Физика - экспериментальная наука. Она основывается на экспериментально установленных фактах. Факты остаются, а их интерпретация может со временем меняться. Факты устанавливаются из наблюдений и опытов, которые в свою очередь приобретают особую ценность, когда они выражают физические величины числами, которые порождаются измерениями.

Измерением называют процесс сравнения параметров измеряемого объекта с такими же параметрами эталонного объекта (измерительного прибора). Следует различать два способа измерения. Прямое - при котором непосредственно измеряются требуемые параметры, например, линейные размеры тела, вес, сопротивление и т.д. Косвенное - при котором требуемую величину вычисляют по формуле содержащей непосредственно измеренные величины.

Ясно, что по самому своему определению измерение (сравнение) не дает точного, истинного значения измеряемой величины, которое обозначим через 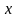- измерение всегда осуществляется с ошибками (погрешностями). В свою очередь точность измерений зависит от способов контроля и обработки ошибок.

Контроль ошибок, помимо методов стандартизации измерительных приборов, включает, также, классификацию ошибок. Различают три типа ошибок, возникающих при измерениях: грубые ошибки или промахи, систематические и случайные.

Промахи - ошибки, сделанные вследствие неверной записи результата измерения, неправильно прочитанного показания прибора и т.д. Их источником, как правило, является невнимание, неаккуратность экспериментатора.

Систематические ошибки вызываются факторами, действующими одинаковым образом при многократном проведении одних и тех же измерений. Их величина одинакова во всех измерениях, проводящихся одним и тем же методом с помощью одних и тех же измерительных приборов. Причиной возникновения систематических ошибок может служить, например, неисправный измерительный прибор, которым производятся измерения.

Случайные - ошибки возникающие вследствие причин, действие которых неодинаково в каждом измерении и не может быть учтено. Их величина различна даже для измерений, выполненных одинаковым образом.

Данная разработка посвящена описанию статистических методов обработки случайных ошибок, решению вопроса о точности измерений и оценке истинных значений измеряемых величин.

Результат измерения и математическое ожидание результата

Если отдельные наблюдения дают несколько отличные друг от друга результаты, то мы имеем дело с ситуацией, когда случайная погрешность играет существенную роль. Наличие случайно действующих факторов приводит к тому, что результаты отдельных наблюдений представляют собой случайные величины, колеблющиеся вокруг, некоторого среднего значения. За результат измерения принимают среднее арифметическое результатов наблюдений, в которые предварительно введены поправки для исключения систематических погрешностей, т.е.

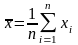, (1)

где 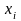- результат наблюдения; - конечное число наблюдений. Формула (1) определяет так называемое выборочное среднее значение случайной величины. Чем больше произведено наблюдений, тем более устойчив и менее подвержен влиянию случайных факторов средний результат, так как положительные и отрицательные погрешности отдельных наблюдений в какой-то степени компенсируют друг друга. Если вообразить, что число результатов наблюдений бесконечно, то тогда средний, результат будет абсолютно устойчивый, т.е. выразится вполне определенным, не случайным числом. Это число называют математическим ожиданием результата. В математической статистике его называют генеральным средним значением случайной величины.

Итак, математическим ожиданием результата измерений называется среднее значение бесконечно большого числа результатов наблюдений. Обозначим его буквой .

Совпадает ли с истинным значением измеряемой величины? Поскольку математическое ожидание - это результат, освобожденный от случайных погрешностей, и поскольку существуют еще систематические погрешности, то мы придем к выводу, что 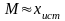. А на какую величину они отличаются? На величину систематической погрешности, если таковая присутствует.

Теперь можно дать еще одно определение систематической погрешности: систематической погрешностью 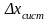называется разность между математическим ожиданием результата и истинным значением измеряемой величины, т.е.

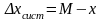(2)

Среднее значение конечного числа измерений 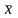отличается от математического ожидания измеряемой величины. Разность между ними и есть случайная погрешность среднего арифметического результатов измерений:

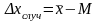(3)

Случайной погрешностью наблюдения называется разность между результатом наблюдения и математическим ожиданием результата:

.
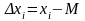