1.1.Одноканальная модель смо с ожиданием

Система массового обслуживания имеет один канал. Входящий поток заявок на обслуживание - простейший поток с интенсивностью . Интенсивность потока обслуживания равна  (т. е. в среднем непрерывно занятый канал будет выдавать  обслуженных заявок). Длительность обслуживания - случайная величина, подчиненная показательному закону распределения. Поток обслуживаний является простейшим пуассоновским потоком событий. Заявка, поступившая в момент, когда канал занят, становится в очередь и ожидает обслуживания.

Предположим, что независимо от того, сколько требований поступает на вход обслуживающей системы, данная система (очередь + обслуживаемые клиенты) не может вместить более N требований (заявок), т. е. клиенты, не попавшие в ожидание, вынуждены обслуживаться в другом месте. Наконец, источник, порождающий заявки на обслуживание, имеет неограниченную (бесконечно большую) емкость.

Граф состояний СМО в этом случае имеет вид, показанный на рис. 5.2.

Рис. 0.2. Граф состояний одноканальной СМО с ожиданием (схема гибели и размножения)

Состояния СМО имеют следующую интерпретацию:

S₀ –­­ «канал свободен»;

S₁ ­–­­­ «канал занят» (очереди нет);

S₂ – «канал занят» (одна заявка стоит в очереди);

S_k – «канал занят» (k-1 заявок стоит в очереди);

S_m+1 – «канал занят» (m заявок стоит в очереди).

Стационарный процесс в данной системе будет описываться следующей системой алгебраических уравнений:

Пользуясь уравнениями для процесса гибели и размножения получим:

(0.0)

где – приведенная интенсивность (плотность) потока;

Тогда вероятность что занят 1 канал и k-1 мест в очереди:

Следует отметить, что выполнение условия стационарности < 1 для данной СМО не обязательно, поскольку число допускаемых в обслуживающую систему заявок контролируется путем введения ограничения на длину очереди (которая не может превышать m), а не соотношением между интенсивностями входного потока, т. е. не отношением .

Определим характеристики одноканальной СМО с ожиданием и ограниченной длиной очереди, равной m:

вероятность отказа в обслуживании заявки;

; (0.0)

относительная пропускная способность системы:

; (0.0)

абсолютная пропускная способность:

А = q; (0.0)

среднее число заявок, находящихся в очереди:

; (0.0)

среднее число заявок, находящихся под обслуживанием:

(0.0)

среднее число заявок, находящихся в системе(связанных с СМО):

; (0.0)

среднее время пребывания заявки в системе:

Т_сист.= Т_ож. + t_об; (0.0)

средняя продолжительность пребывания клиента (заявки) в очереди:

. (0.0)

Если имеется неограниченное число мест ожидания в очереди m, то вышеуказанные формулы справедливы только при ρ < 1, так как при ρ 1 нет установившегося режима (очередь неограниченно растет) и при q=1, A=λq=λ.

1.2.Многоканальная модель смо с ожиданием

Процесс массового обслуживания при этом характеризуется следующим: входной и выходной потоки являются пуассоновскими с интенсивностями  и  соответственно; параллельно обслуживаться могут не более n клиентов. Система имеет n каналов обслуживания. Средняя продолжительность обслуживания одного клиента равна 1/.

Рис. 0.3. Граф состояний многоканальной СМО с ожиданием

Состояния системы будем нумеровать по числу заявок, связанных с системой:

По стрелкам слева направо систему переводит всегда один и тот же поток заявок с интенсивностью λ, по стрелкам справа налево систему переводит поток обслуживаний, интенсивность которого равна µ, умноженному на число занятых каналов.

Решение будет действительным, если выполняется следующее условие: .

Вероятностные характеристики функционирования в стационарном режиме многоканальной СМО с ожиданием и неограниченной очередью определяются по следующим формулам.

Вероятность того, что все посты свободны:

при неограниченной длине очереди:

(0.0)

при длине очереди ограниченной числом m:

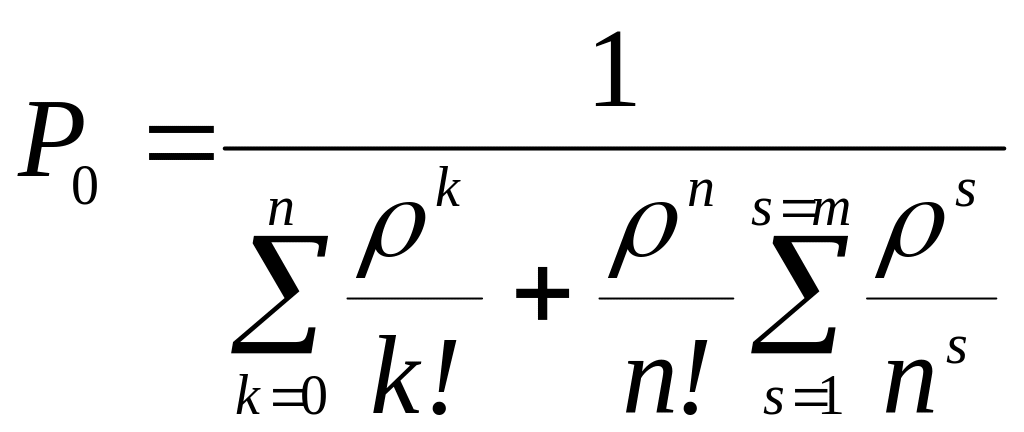; (0.0)

вероятность отказа система (все посты заняты, все места в очереди заняты):

; (0.0)

вероятность того, что занято k постов и r постов ожидания:

; (0.0)

; (0.0)

среднее число заявок в очереди:

, (0.0)

где ;

среднее число занятых каналов:

(0.0)

складывая среднее число заявок в очереди и среднее число занятых каналов , получим среднее число заявок, связанных с системой:

; (0.0)

среднее время ожидания заявки в очереди:

; (0.0)

средняя продолжительность пребывания заявки в системе:

t_сист = +1/.. (0.0)