Построение временных задержек

Реакция LTI-модели на сформированный импульсный сигнал реализуется на основе функции lsim в следующих формах:

lsim(sys,u,t) impulse(sys,u,t,x0)

[y,t,x] = lsim (sys,u,t,x0)

где t - вектор-строка моментов времени; u - вектор-строка значений входного сигнала, а остальные параметры аналогичны ранее рассмотренным функциям.

Для компенсации влияющих факторов используются стандарт-сигналы, реализуемые на основе функции gensig в следующих формах:

[u,t]= gensig(type,tay) [u,t]= gensig(type,tay,Tf,Ts),

где type – строковая переменная, задающая тип сигнала (‘sin’ – синусоиды; ‘square’ – прямоугольной формы; ‘pulse’ – периодических импульсов) с единичной амплитудой; tay и Tf – период и продолжительность сигнала (с); Ts – период дискретности генератора импульсов (с).

Рассмотрим пример формирования на основе функции gensig прямоугольного сигнала с периодом 5 с, продолжительностью 30 с и периодом дескритизации 0,1 с. На рис. 19 представлены исходные результаты формирования сигнала.

Рис. 19. График импульсного стандарт-сигнала

При заданных параметрах матрицы передаточной функции

найдем реакцию на сформированный сигнал, как показано на рис. 20:

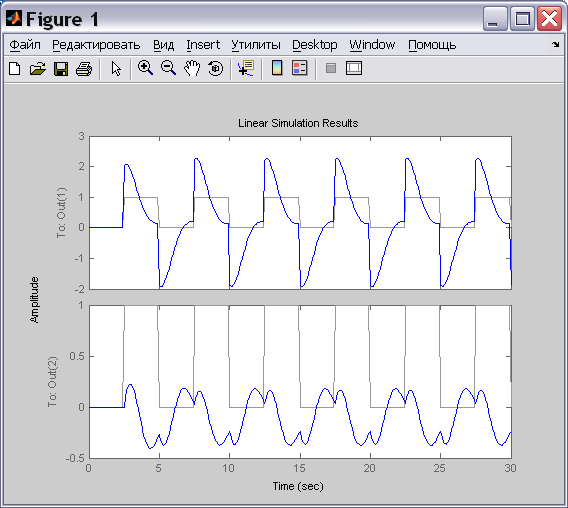
Рис. 20. Графики реакции двумерного объекта на периодический прямоугольный сигнал

Задание 12. Выполните операции вычисления реакции двумерного объекта на периодический прямоугольный сигнал.

Определение временных задержек осуществляется на основе 4-х функций: delay2z (определения дискретных задержек), hasdelay (определения наличия задержек), totaldelay (определение суммарных задержек) и pade (для формирования Паде аппроксимации). Например, при определении дискретных задержек достаточно выполнить команды (рис. 21):

Рис. 21. Пример выполнения функции delay2z

Задание 13. Выполните операции определения задержек с использованием разных функций.

Моделирование частотного отклика систем

Для моделирования частотного отклика систем используется группа функций, назначение которых представлено в таблице 2.

Таблица 2. Перечень функций для моделирования частотного отклика систем

Наимен-ие	Выполняемые операции
allmargin	служит для расчета и построения частотного отклика системы
bode	формирует диаграмму Боде (графики ЛАЧХ и ФЧХ)
evalfr	вычисляет значение комплексного коэффициента передачи для одного заданного комплексного значения частоты
fregresp	вычисляет значение комплексного коэффициента передачи для заданного набора частот
linspace	формирует вектор-строку линейно-возрастающих частот
logspace	формирует вектор-строку логарифмически возрастающих частот
ltiview	открывает окно просмотра LTI-моделей
margin	вычисляет запасы устойчивости по фазе и амплитуде

Рассмотрим пример построения диаграммы Боде для узкополосной системы (рис. 22):

Рис. 22. График примера построения диаграммы Боде для узкополосной системы

Задание 14. Выполните операции построения диаграммы Боде для узкополосной системы.

Рассмотрим пример определения запаса устойчивости по логарифмической амплитудно-частотной характеристике (ЛАЧХ) с помощью функции margin, как приведено на рис. 23:

Рис. 23. Пример построения ЛАЧХ на основе функции margin

Задание 15. Выполните операции построения ЛАЧХ на основе функции margin.

Функция norm используется для вычисления норм типа или для непрерывной или дискретной LTI-модели (норма равна бесконечности для неустойчивых систем) и применяется в следующих формах:

norm(sys) norm(sys,2) norm(sys,inf)

norm(sys,inf,tol) [ninf,fpeak]= norm(sys)

Норма для устойчивой непрерывной системы с передаточной матрицей W(p) есть квадратный корень из среднего значения квадрата импульсной характеристики системы, а с переходом к преобразованию Лапласа данная норма (по теореме Парсеваля) определяется соотношением:

где tr{*} – обозначение следа матрицы, - матрица, сопряженная относительно . При этом норма равна максимальному значению модуля частотной характеристики:

- - для одномерных моделей; или - для многомерных моделей, где максимальное сингулярное число матрицы , т.е. неотрицательный корень квадратный из максимального собственного числа матрицы ;

- .

Функция norm использует следующие аргументы: sys – имя модели; 2 – задание нормы ; inf - задание нормы ; tol – точность при расчете нормы (при умолчании tol = 1е-2).

К формируемым величинам относятся: ninf – норма модели (при умолчании - ); fpeak – частота, на которой норма достигает максимального значения.

Рассмотрим пример применения функции norm:

Рассмотрим использование функции sigma для построения частотной характеристики сингулярных чисел непрерывной модели матрицы . При этом формы описания функции аналогичны вышерассмотренным:

sigma(sys) sigma(sys,w) sigma(sys,w,type)

sigma(sys1,sys2,…,sysN) sigma(sys1,sys2,…,sysN,w)

sigma(sys1,sys2,…,sysN,w,type)

[sv,w]= sigma(sys) [sv]= sigma(sys,w) и др.

На рис. 24 представлен пример графиков частотных характеристик для сингулярных точек системы

Рис. 24. Пример выполнения функции sigma

Задание 16. Выполните операции построения частотной характеристики сингулярных чисел модели.