Определение устойчивости систем в пакете Control System

Функция eig позволяет вычислить полюсы LTI-модели в формах:

d = eig(A) d = eig(A,B) [V,D] = eig(A) [V,D] = eig(A,B)

[V,D] = eig(A,B,flag) [V,D] = eig(A,’nobalance)

Рассмотрим примеры реализации этой функции (рис. 11):

Рис. 11. Пример использования функции eig

Задание 4. Выполните операции вычислений с помощью функции eig.

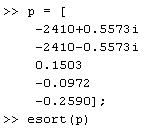
Функция esort используется для сортировки полюсов непрерывной LTI-модели в порядке убывания значений их действительной части в формах:

s = esort(p) [s,ndx]= esort(p)

Неустойчивые полюсы располагаются в начале списка. В этой функции р есть вектор-строка полюсов модели; s – вектор, содержащий отсортированные полюсы; ndx - вектор, содержащий индексы, используемые при сортировке. На рис. 12 представлены результаты использования функции esort:

Рис. 12. Пример использования функции esort

Задание 5. Выполните операции сортировки неустойчивых полюсов.

Функция pzmap формирует карту нулей и полюсов с выполнением следующих команд:

При дополнительном использовании функции rlocus можно выполнить расчет и построить корневой годограф по известной LTI-модели с выполнением команд:

Но для получения удобочитаемой формы графической иллюстрации с построением сетки окна удобнее воспользоваться функцией sgrid (рис. 13):

Рис. 13. Пример построения карты нулей и полюсов

Задание 6. Выполните пример построения карты нулей и полюсов.

Функция sgrid и sgrid(z,wn) также выполняют построение сетки окна на z-плоскости, например, как показано на рис. 14:

Рис. 14. Пример построения карты нулей и полюсов на основе функций rlocus и sgrid

Задание 7. Выполните операции построения сетки окна на z-плоскости.

Построение диаграммы Найквиста (годографа) осуществляется на основе функции nyquist в следующих формах записи:

nyquist(sys) nyquist(sys,w)

nyquist(sys1, sys2,… sysN) nyquist(sys1, sys2,… sysN,w)

[re,im,w]= nyquist(sys) [re,im]= nyquist(sys,w)

Где w – вектор частот; re и im векторы значений вещественной и мнимой частей комплексного коэффициента передачи для заданного набора частот.

На рис. 15 представлен пример построения диаграммы Найквиста:

Рис. 15. Пример построения диаграммы Найквиста

Задание 8. Выполните операции построения диаграммы Найквиста.

Построение диаграммы Николса (годографа) на основе функции nichols используется также в разных формах записи:

nichols(sys) nichols (sys,w)

nichols (sys1, sys2,… sysN) nichols (sys1, sys2,… sysN,w)

[mag,phase,w]= nichols (sys) [mag,phase]= nichols (sys,w)

На рис. 16 представлен пример построения диаграммы Николса

Рис. 16. Пример построения диаграммы Николса

Задание 9. Выполните операции создания диаграммы Николса.

Анализ показателей качества управления Анализ переходных и импульсных характеристик

Функция step позволяет рассчитать и построить реакцию модели на единичную ступенчатую функцию, т.е. формирует переходную функцию системы в следующих формах:

step(sys) step(sys,t)

step(sys1, sys2,…, sysN,) step(sys1, sys2,…, sysN,t)

step(sys1, ‘PlotStyle1’,…, sysN, ‘PlotStyleN’)

[y,t,x] = step(sys)

В качестве примера использования этой функции поостроим графики переходных процессов для модели второго порядка:

На рис. 17 представлен пример решение такой задачи с применением функции step:

Рис. 17. График переходных характеристик системы 2-го порядка

Задание 10. Выполните операции расчета и построения реакции модели на единичную ступенчатую функцию..

Формирование импульсной характеристики модели (или нескольких их видов) с использованием функции impulse, формируемых как

impulse(sys) impulse(sys,t)

impulse(sys1, sys2,…, sysN,) impulse (sys1, sys2,…, sysN,t)

impulse(sys1, ‘PlotStyle1’,…, sysN, ‘PlotStyleN’)

[y,t,x] = impulse (sys)

Решение данной задачи выполняется на предыдущем примере модели 2-го порядка (1), как указано на рис. 18:

Рис. 18. График импульсных характеристик системы 2-го порядка

Задание 11. Выполните операции расчета и построения импульсных характеристик системы 2-го порядка.