6. Влияние отражения радиоволн от гладкой поверхности Земли.

Влияние отражения радиоволн от гладкой поверхности Земли выражается через множитель ослабления, обусловленный интерференцией прямой и отражённой от гладкой поверхности Земли волн в предположении, что r < R_пр. Для коротких пролетов, когда r < 0,2R_пр можно пренебречь сферичностью Земли и считать её плоской (Рис.2.6.1).

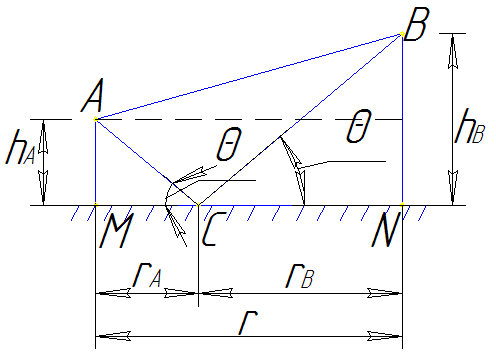
Рис.2.6.1

Передающая антенна расположена в точке А на высоте h_A, имеет коэффициент усиления равный G_T и излучает мощность Р_изл. Найдем напряженность поля в точке В, расположенной на высоте h_В над поверхностью Земли и лежащей в направлении максимального излучения передающей антенны.

Будем считать, что высоты подвеса антенн и .

В точку приёма В приходят две волны – прямая и отраженная от поверхности Земли в точке С, положение которой определяется равенством углов скольжения q.

Комплексная амплитуда прямой волны, пришедшей в точку приёма В

(19)

где r_пр = АВ – длина пути, проходимого прямой радиоволной.

Комплексная амплитуда отражённой волны

(20)

где r_отр = АС + СВ, модуль коэффициента отражения радиоволны от земной поверхности, фазовый сдвиг при отражении радиоволны от земной поверхности.

Т.к. разность длины хода прямой и отражённой волнами не очень большая, то при определении их амплитуд будем полагать, что r_пр » r_отр » r.

Тогда для комплексной амплитуды напряженности поля, образованного взаимодействием прямой о отраженной волн в точке приема В можно записать

_{. ,}

_или

₍₂₁₎

где - разность хода отраженной и прямой волн.

Отсюда комплексный множитель ослабления будет иметь вид

_, (22)

а его модуль

(23)

Следовательно, для определения множителя ослабления необходимо знать величину модуля и фазы коэффициента отражения волны от земной поверхности, а также разность хода прямой и отражённой волн.

Разность хода можно выразить через высоты поднятия антенн над земной поверхностью и длину пролета. Из Рис.2.6.1 следует

_{, (24)}

учитывая, что , и , тогда выражение для разности хода будет иметь вид

(25)

С учётом формулы (25) выражения (22) и (21) запишутся в следующем виде:

(26)

. (27)

Формулы (22), (23), (26) и (27) называются интерференционными, т.к. при изменении любой из величин , определяющих разность хода прямых и отражённых волн, и, следовательно, условия их интерференции, соответствующие изменения множителя ослабления носят осциллирующий характер, при котором имеют место интерференционные минимумы и максимумы (Рис.2.6.2).

Интерференционный максимум появляется при условии, что прямая и отражённая волны приходят в точку приёма В с одинаковыми фазами т.е.

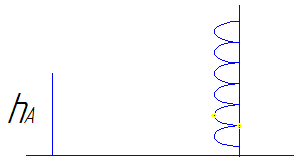
Рис.2.6.2

При этом модуль множителя ослабления

_{, (29)}

_{где Фm – модуль коэффициента отражения для m-го максимума.}

Если прямая и отражённая волны приходят в точку приёма В в противофазе, т.е.

(30)

то имеет место интерференционные минимумы, при которых модуль множителя ослабления

₍₃₁₎

_где модуль коэффициента отражения для n-го минимума.