3. Область пространства, существенно участвующая в формировании поля на заданной линии связи.

Эллипсоид существенный для распространения радиоволн.

Для выделения из всего пространства той его области, которая существенна для распространения радиоволн, от источника А к точке В необходимо провести расчет поля с помощью принципа Гюйгенса – Кирхгофа, разделив пространство на зоны Френеля.

Согласно принципу Гюйгенса-Френеля, каждый элемент фронта волны является воображаемым вторичным источником сферической волны (элементом Гюйгенса), который по представлениям Френеля обладает направленным излучением с максимумом в направлении, перпендикулярном поверхности фронта и нулевым излучением в обратном направлении.

Определим поле в точке приёма, суммируя поля вторичных источников. Согласно теореме Кирхгофа, достаточно просуммировать поля источников, распределённых на воображаемой замкнутой поверхности, которая охватывает или источник А или точку приёма В.

Выберем поверхность, которая охватывает источник, и составим её из бесконечной плоскости S₀, расположенной перпендикулярно линии АВ (Рис.1.4.3) и полусферы бесконечного радиуса, которая замыкает плоскость S₀.

Вклад источников, распределённых на бесконечно удалённых участках поверхности , будет бесконечно мал, и поле формируется источником на поверхности , расположенном на конечном расстоянии от точки приёма.

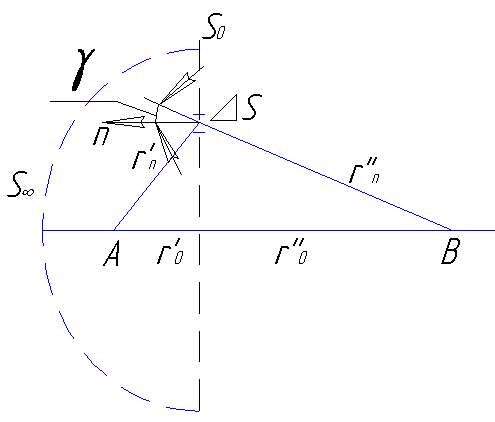
Рис.1.4.3

Суммарное действие источников элемента поверхности оценивается суммой элементарных составляющих поля с амплитудой и фазой , где С – постоянная, зависящая от свойств первичного источника.

Суммарное поле от всех источников рассчитывается с учётом их распределения по зонам Френеля на плоскости .

На Рис.1.4.4 показано векторное суммирование элементарных составляющих DЕ, возбуждаемых источниками двух зон Френеля с номерами n и n+1.

Рис.1.4.4.

Расчёты показывают, что результирующие векторы полей отдельных зон коллинеарны, при этом векторы соседних зон направлены противоположно из-за различия на длин путей от симметричных участков зон до точки В.

Амплитуда вектора поля , поскольку расстояние и с увеличением уменьшается значение .

В результате коллинеарности векторов полей от отдельных зон амплитуда результирующего поля определяется алгебраическим суммированием, при этом учёт фазы приводит к знакопеременному ряду. Каждый член ряда равен амплитуде поля, наведённого в точке наблюдения источниками n-й зоны Френеля.

Для выявления количественных соотношений удобно записать ряд в виде

(6)

Поскольку соседние члены ряда мало отличаются друг от друга, то значение поля в каждый из скобок (6) близко к нулю и в первом приближении результирующее поле будет равно:

, , (7)

т.е. в принятом приближении напряжённость поля равна половине той величины, которая создаётся источниками первой зоны. Другая половина, а также поля от других источников высших зон взаимно компенсируются за счёт противофазности полей смежных зон.

Результат последовательного от зоны к зоне алгебраического суммирования полей представлен на графике Рис. 1.4.5.

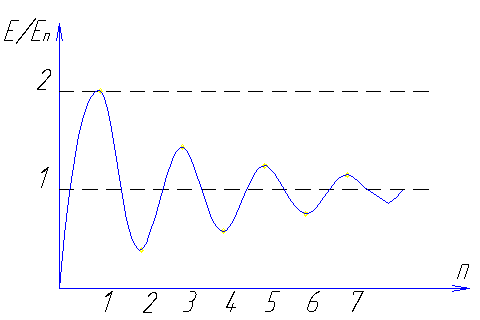
Рис. 1.4.5

При суммировании полей от источников только первой зоны напряжённость поля плавно возрастает до , где - напряжённость поля в свободном пространстве. При дальнейшем сложении проявляется действие противофазных полей 2-й зоны и результирующее поле уменьшается. Компенсирующее действие полей четных зон обуславливает немонотонный закон приближения величины . Максимальные значения поля Е наблюдаются при ограничении области распространения радиусом нечётной зоны Френеля, а минимальные значения – чётной.

В результате суммирования поле в точке приёма создаётся в основном вторичными источниками первых зон Френеля, что и приводит к понятию существенной области распространения.

Существенную область ограничивают примерно восьмью первыми пространственными зонами Френеля, называя её существенным эллипсоидом. При таком приближении ошибка в определении поля не превышает 16%.

Максимальный радиус существенного эллипсоида соответствует середине трассы и согласно формуле (3) для зоны

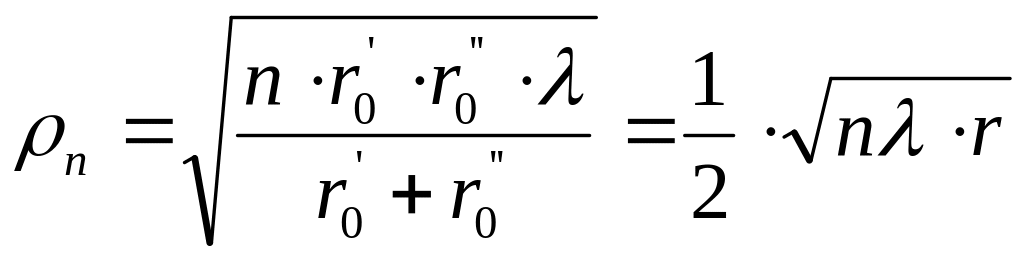(8)

В прикидочных расчетах существенную область ограничивают эллипсоидом первой зоны с максимальным радиусом

. (9)

Чем короче волна, тем меньше поперечные размеры существенного эллипсоида. Например, на волнах l = 10 м – 10 см при протяженности линии связи r = 10 км радиус r_1max = 160 – 16 м. При этом большая ось существенного эллипсоида, соизмеримая с длиной радиолинии в сотни и тысячи раз больше его малой оси, т.е. эллипсоид сильно вытянут вдоль трассы.

Понятие существенной зоны широко применяется при изучении условий распространения на линиях, где электрические параметры трассы распространения неоднородны. Одной из типичных задач является исследование условий распространения волны при разных высотах поднятия над Землей антенны. Например, на линии протяженностью 40 км при работе на волне 10 см радиус существенной области r_1max = 32 м. При этом ослабление поля зависит от степени затенения существенной области неровностями земной поверхности. Если высоты подвеса антенн таковы, что часть существенной области затенена поверхностью Земли, то потери на линии связи значительно возрастают.