

Министерство образования Российской Федерации
Национальный минерально-сырьевой университет «Горный»

Кафедра общей технической физики. Отчет по лабораторной работе №6 Определение момента инерции с помощью маятника Обербека
Выполнил: студент гр. ЭРС-12-2 ______________ /Слотин А.С./
(подпись) (Ф.И.О.)
Проверил: ассистент ____________ /Дашина а.Ю./
(должность) (подпись) (Ф.И.О.)
Санкт-Петербург
2013 год
Цель работы – исследовать зависимость момента инерции крестовины с надетыми на нее грузиками от распределения массы относительно оси вращения, проходящей через центр масс.
Краткое теоретическое содержание
В основе эксперимента лежит основное уравнение динамики вращательного движения твердого тела
![]() (1)
(1)
где М - суммарный момент внешних сил, приложенных к телу относительно оси вращения; J - момент инерции тела относительно той же оси; - угловое ускорение.
В динамике вращательного движения различают два понятия: момент силы относительно точки и момент силы относительно оси вращения.
Момент силы относительно точки О определяется как векторное произведение
![]() ,
,
где
![]() -
сила,
-
сила,
![]() -
радиус-вектор, проведенный из точки О,
в точку приложения силы.
-
радиус-вектор, проведенный из точки О,
в точку приложения силы.
Момент силы
относительно оси вращения есть
проекция
![]() на произвольную ось z,
которая проходит через точку О:
на произвольную ось z,
которая проходит через точку О:
![]()
![]() .
.
Момент инерции тела является мерой инертности тела при вращательном движении, подобно тому как масса тела является мерой инертности тела при поступательном движении. Момент инерции тела зависит от распределения массы тела относительно оси вращения. Для вычисления момента инерции твердого тела относительно данной оси разобьем мысленно тело на большое число весьма малых элементов - материальных точек (рис.1). Тогда момент инерции тела

![]()
или
![]() ,
,
где mi - масса элемента; ri - расстояние от элемента до оси вращения; - плотность вещества в элементе объема dV, находящегося на расстоянии r от оси вращения. Таким образом, задача нахождения момента инерции сводится к интегрированию.
Из формулы (1) следует, что угловое ускорение вращающегося тела прямо пропорционально моменту внешних сил М и обратно пропорционально моменту инерции J. Следует подчеркнуть, что момент инерции не зависит ни от момента внешних сил М, ни от углового ускорения.
Маятник Обербека состоит из крестовины, на стержнях которой находятся грузы. Они могут перемещаться по стержням и закрепляться в нужном положении (рис.2 ). Крестовина с грузами насажена на вал, на котором укреплены два шкива различного радиуса. На шкив намотана нить, которая переброшена через блок. К ее концу привязана гирька, момент силы тяжести которой уравновешивает момент сил трения (вес этой гирьки в расчетах не учитывается).
К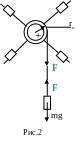 концу нити подвешивают груз массой m,
под действием силы тяжести которого
система приводится в движение. На груз
действует сила тяжести P=mg
и сила натяжения F,
поэтому на основании второго закона
Ньютона можно записать
концу нити подвешивают груз массой m,
под действием силы тяжести которого
система приводится в движение. На груз
действует сила тяжести P=mg
и сила натяжения F,
поэтому на основании второго закона
Ньютона можно записать
![]() (2)
(2)
где g - ускорение свободного падения; а - ускорение, с которым движется груз.
Крестовина приходит во вращательное движение под действием момента силы натяжения
М = Frо , (3)
где rо - радиус шкива.
Из уравнений (1)-(3) можно получить
![]() ,
(4)
,
(4)
Так как угловое ускорение связано с ускорением а соотношением = а/r0 , то формулу (4) можно записать в виде
![]() ,
(5)
,
(5)
где а = 2h/t2; h - путь, пройденный грузом за время t.
Таким образом,
.
![]() (6)
(6)
Законы и соотношения, используемые при выводе рабочих формул
Основное уравнение динамики вращательного движения твердого тела
![]()
где
М - суммарный момент внешних сил (![]() ),
приложенных к телу относительно оси
вращения; J
- момент инерции тела (
),
приложенных к телу относительно оси
вращения; J
- момент инерции тела (![]() )
относительно той же оси;
- угловое ускорение (
)
относительно той же оси;
- угловое ускорение (![]() ).
).
Второй закон Ньютона: ускорение, с которым движется тело, прямо пропорционально силе, действующей на тело, совпадает с ней по направлению и обратно пропорционально массе тела.
![]() - 2 закон Ньютона в импульсной форме
- 2 закон Ньютона в импульсной форме
![]() ,
при m=const
,
при m=const
