2. Динамическое исследование движения системы

Приведенный к начальному звену - кривошипу О₁А - момент сил сопротивлений с отношениями скоростей в виде отрезков планов выражаем формулой [1]

, [1]

где М - приведенный момент сопротивления, Нм;

P_сi - сила сопротивления для рабочего и холостого ходов, Н;

G_i - сила тяжести масс соответствующего звена, Н;

p –полюс плана скоростей;

, - изображения на планах скоростей механизма проекций скоростей точек приложения сил на линии действия соответствующих сил, мм;

=40 мм - изображение скорости кривошипной точки A, мм;

r_A=OA - радиус кривошипа, м.

В составляющих момента от сил тяжести масс звеньев знак «плюс» соответствует направлению вектора вверх, знак «минус» – направлению вектора вниз.

В качестве примера для одного положения выполняем численные расчеты приведенных моментов сил сопротивлений. Изображения скоростей на планах в миллиметрах чертежа получены в кинематическом исследовании механизма.

Для такта холостого хода (расчет в положении 2)

Для такта рабочего хода (расчет в положении 8)

Результаты расчетов приведенного момента сил сопротивлений по формуле (1) за цикл движения механизма представлены в табл. 2.

Таблица 2. Результаты расчёта приведённого момента сопротивлений

Положения		0	1	2	3	4	5	6	7	8	9	10	11	12
Fп с	Н	2500	2500	2500	2500	2500	2500	6000	6000	6000	6000	6000	6000	6000
	мм	50
	мм	0	53	63	46	22	17	10	23	34	37	45	33	0
	мм	0	-24	-25	-13	-14	-3	19	28	25	23	6	-9	0
	мм	0	-4	-7	-10	-8	-5	5	8	9	9	2	-3	0
	мм	0	-3,5	-6	-9	-7	-3	4,5	7,5	8	7	1	2,5	0
	Н	981
	Н	1471,5
	Н	1962
Мсс	Нм	0	240,5	277,25	174,69	39,4	80,49	247	479,88	643,7	678,85	701,9	449,6	0
	мм	0	48	55	35	8	16	47	96	129	136	140	99	0

С троим график ММ() на чертеже (см. л. 1, ТММКП рис.1) с необходимой крупностью изображений в масштабах моментов сил _М и углов μ_φ.

г де М_max - максимальный момент, Нм;

_max – его черчежное изображение на графике, мм;

240 мм – изображение одного оборота кривошипа на графике моментов сил.

Интегрированием [1] приведенного момента сил по углу положения начального звена строим график работ приведенных сил сопротивлений в масштабе

_Аh _М _,

где _А в Дж/мм;

h – полюсное расстояние при интегрировании, мм.

_А=8050,0262 = 10,48 Дж/мм.

С учетом постоянного момента движущих сил строим прямолинейный график работ этих сил, исходя из того, что за цикл установившегося движения системы сумма работ сил сопротивлений и движущих сил равна нулю. Дифференцированием графика работ движущих сил по углу положения начального звена получаем в масштабе на графике момент движущих сил.

Алгебраическим суммированием ординат графиков работ приведенных сил сопротивлений и движущих сил строим масштабный график избыточных работ исследуемой системы.

Таблица 3. Результаты расчёта избыточной работы.

Положения		0	1	2	3	4	5	6	7	8	9	10	11	12
А	мм	0	9	13	18	29	42	50	59	38	23	5	-6	0
А	Дж	0	94	136	189	304	440	524	618	398	241	52	-63	0

Составляем расчетную формулу приведенного к начальному звену момента инерции системы

[2]

где J_Si - момент инерции звена относительно оси S_i в кгм^;

m_i - масса звена, кг.

По формуле (3) рассчитаем постоянную часть приведенного момента инерции и выделим переменную часть в функции угла положения начального звена.

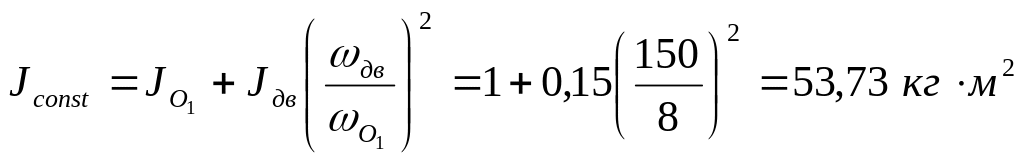[3]

[4]

где - момент инерции начального кривошипа относительно оси О, кгм²;

J_дв - момент инерции ротора двигателя, кгм^;

_дв - угловая скорость ротора, рад/с.

₁ - угловая скорость начального кривошипа, рад/с.

Для данного механизма формулу (4) представим в удобном для расчетов виде где отдельные составляющие по звеньям получают выражения

где m=m₅ холостого хода, а для рабочего - m=m₅ + m_M .

Для примера расчеты выполняем в положений 2 и 8.

Приведенный момент инерции.

Результаты расчетов за цикл движения механизма представлены в табл. 4.

Таблица 4. Результаты приведённого момента инерции

Положения		0	1	2		3	4	5	6	7	8	9	10	11	12
	кг м2	1
	кг м2	0,15
	с-1	150
	с-1	8
		2
	кг м2	1,5
	кг м2	100
	с-1	1,74	3,04	3,00		0,91	0,65	1,52	1,91	1,87	1,52	0,65	0,44	0,44	1,74
	с-1	0,00	3,39	4,27		3,27	1,70	0,48	0,85	1,82	2,42	2,00	2,73	1,94	0,00
	с-1	0,00	0,09	0,13		0,21	0,14	0,05	0,08	0,16	0,17	0,18	0,03	0,05	0,00
m2	кг	100
m3	кг	150
m4	кг	200
m5	кг	500
mM	кг	1000
	м/с	0,4	0,68	0,90	0,92		0,66	0,46	0,40	0,58	0,72	0,62	0,84	0,72	0,4
	м/с	0,00	0,56	0,68	0,56		0,28	0,10	0,14	0,30	0,40	0,44	0,46	0,36	0,00
	м/с	0,00	1,10	1,30	0,98		0,50	0,14	0,22	0,50	0,72	0,78	0,90	0,66	0,00
	м/с	0	1,08	1,28	0,92		0,44	0,14	0,2	0,48	0,68	0,74	0,90	0,76	0
	кг м2	53,73	53,73	53,73	53,73		53,73	53,73	53,73	53,73	53,73	53,73	53,73	53,73	53,73
	кг м2	0,34	20,11	21,12	12,09		3,27	0,54	1,53	7,14	13,9	15,94	23,3	16,11	0,34
	кг м2	54,07	73,84	74,85	65,82		57,00	54,27	55,26	60,87	67,63	69,67	77,03	69,84	54,07
	мм	2	134	140	81		22	4	10	48	93	106	155	107	2

Строим на чертеже график приведенного момента инерции (J_v) системы в функции угла положения начального звена в масштабе

Учитывая последующую необходимость исключения углового параметра, оси графика изображаем повернутыми на 90 по часовой стрелке (см. график моментов инерции на листе 1 КПР ТММ).

Решением дифференциального уравнения движения системы в форме квадратуры получена формула [5] для расчетов угловой скорости начального кривошипа в каждом положении механизма

[5]

где Т _T, Дж, учитывая знак;

- изображения избыточной энергии на графике, мм;

J_() и _ - соответственно приведенный момент инерции системы и угловая скорость звена приведения в начале цикла движения (в положении 0), принимаемая равной заданному среднему ее значению.

Д ля примера в 2-ом положении угловая скорость кривошипа рассчитывается по формуле [2]

Результаты расчетов избыточной энергии и угловой скорости начального звена по формуле [6] за цикл движения механизма представлены в табл. 5.

Таблица 5. Результаты расчёта угловой скорости

Положения	0	1	2	3	4	5	6	7	8	9	10	11	12
Т, Дж	0	94,32	136,24	188,64	303,92	440,16	524,00	618,32	398,24	241,04	52,40	-62,88	0,00
, кгм2	54,07	54,07	54,07	54,07	54,07	54,07	54,07	54,07	54,07	54,07	54,07	54,07	54,07
0, рад/с	8	8	8	8	8	8	8	8	8	8	8	8	8
, кгм2	54,07	73,84	74,85	65,82	57,00	54,27	55,26	60,87	67,63	69,67	77,03	69,84	54,07
, рад/с	8	7,03	7,06	7,64	8,45	8,94	9,03	8,78	7,93	7,52	6,80	6,91	8
, мм	400	352	353	382	423	447	452	439	397	376	340	346	400

Строим на чертеже график угловой скорости звена приведения в масштабе (откладывая значения от  = 8 рад/с, т.е. начало координат на чертеже по оси ординат равно  = 8 рад/с, см. лист 1 КПР ТММ)

Определяем по графику максимальную и минимальную угловые скорости _max и _min начального звена и по ним находим среднюю за цикл угловую скорость _ср,

рассчитываем коэффициент _ф неравномерности движения механизма, по которому заключаем – нужен ли маховик в данной системе.

Так как  < _ф,то требуется маховик для регулирования движения системы.