3.4. Требования к оформлению отчета
Отчет об индивидуальном задании должен быть оформлен в соответствии с правилами оформления учебных текстовых документов, изложенными в методических указаниях [6]. Его представляют в печатном виде в обложке со стандартным титульным листом, форма которого приведена в Приложении 5.
Расчетно-пояснительная записка включает в себя следующие основные части.
Введение. В нем следует дать общую характеристику роли и значений практических приложений математической статистики.
Задание и исходные данные. Следует конкретизировать постановку задач разделов 1 - 3 задания в соответствии с полученными исходными данными.
Результаты моделирования и исследование статистических характеристик. Эта основная часть работы содержит последовательное решение задач из разделов 1 - 3 задания. При решении каждой задачи следует приводить описание используемого метода, необходимые формулы и пояснения к ним. Если задача решается двумя методами, следует произвести сравнение этих методов и полученных результатов.
Расчеты и результаты представляются в виде таблиц или графиков функций и помещаются в соответствующих разделах записки.
В Приложениях А, Б, и В должны быть помещены полные тексты программ, результатов моделирования и статистического анализа для разделов задания 1, 2, и 3 соответственно.
Библиографический список приводится в конце записки. В тексте самой записки следует делать ссылки на используемую литературу с указанием номера ее в списке (в квадратных скобках).
СПИСОК РЕКОМЕНДОВАННОЙ ЛИТЕРАТУРЫ
Бендат Дж., Пирсол А. Прикладной анализ случайных данных. М.: «Мир», 1989.
Ермаков С.М., Михайлов Г.А. Статистическое моделирование. М.: «Наука», 1982.
Ивченко Г.И., Медведев Ю.И. Математическая статистика. М.: «Высшая школа», 1984.
Коломиец Э.И. Математическая статистика: Метод. указания к решению задач/ Куйбышев. авиац. ин-т. Куйбышев, 1990.
Тараскин А.Ф. Статистическое моделирование и метод Монте-Карло: Учебное пособие/ Самарский гос. аэрокосм. ун-т. Самара, 1997.
Тюрин Ю.Н., Макаров А.А. Статистический анализ данных на компьютере /Под ред. Фигурнова В.Э. М.: «ИНФРА-М», 1998.
Харин Ю.С., Степанова М.Д. Практикум на ЭВМ по математической статистике. Минск: Изд-во «Университетское», 1987.
Суханов С.В. Дипломная работа. Оформление пояснительной записки: Метод. указания / Самарский гос. аэрокосм. ун-т. Самара, 1999.
Приложение 1
Варианты индивидуальных заданий Исходные данные к разделу 1
Вариант |
|
|
|
|
|
1 |
400 |
4.1 |
2.25 |
0.95 |
0.05 |
2 |
350 |
2.6 |
7.29 |
0.96 |
0.01 |
3 |
275 |
0.1 |
14.44 |
0.9 |
0.01 |
4 |
425 |
3.3 |
4.7 |
0.95 |
0.001 |
5 |
450 |
1.15 |
11.56 |
0.92 |
0.02 |
6 |
325 |
4.36 |
3.4 |
0.98 |
0.005 |
7 |
425 |
0.7 |
10.0 |
0.9 |
0.005 |
8 |
350 |
2.2 |
6.76 |
0.99 |
0.001 |
9 |
475 |
1.8 |
9.5 |
0.999 |
0.001 |
10 |
450 |
4.6 |
2.56 |
0.98 |
0.02 |
11 |
375 |
1.2 |
11.7 |
0.99 |
0.005 |
12 |
400 |
3.15 |
4.6 |
0.95 |
0.025 |
13 |
275 |
2.8 |
6.9 |
0.92 |
0.005 |
14 |
325 |
0.65 |
15.21 |
0.96 |
0.025 |
15 |
500 |
3.9 |
4.3 |
0.9 |
0.025 |
16 |
475 |
5.2 |
1.7 |
0.95 |
0.001 |
17 |
425 |
4.75 |
8.5 |
0.9 |
0.02 |
18 |
375 |
0.4 |
11.1 |
0.98 |
0.005 |
19 |
450 |
2.35 |
6.4 |
0.95 |
0.005 |
20 |
325 |
6.0 |
1.1 |
0.99 |
0.001 |
21 |
300 |
5.1 |
1.8 |
0.999 |
0.001 |
22 |
350 |
3.45 |
4.2 |
0.96 |
0.02 |
23 |
275 |
5.15 |
1.25 |
0.99 |
0.005 |
24 |
300 |
5.7 |
1.6 |
0.95 |
0.025 |
25 |
475 |
1.35 |
10.7 |
0.9 |
0.05 |
26 |
400 |
2.1 |
8.41 |
0.999 |
0.05 |
27 |
375 |
1.12 |
12.0 |
0.99 |
0.01 |
28 |
500 |
4.95 |
3.7 |
0.95 |
0.01 |
29 |
300 |
3.7 |
5.4 |
0.98 |
0.001 |
30 |
500 |
0.45 |
9.9 |
0.95 |
0.05 |
Исходные данные к разделу 2
Вариант № 1. Однопараметрическое показательное распределение:
Исходные
данные:
Рассчитать
аналитически:
.
Найти
точечную оценку параметра
методом
моментов.
Вариант № 2. Общее показательное распределение:
Исходные
данные:
Рассчитать аналитически: .
Найти
точечные оценки параметров
и
методом моментов.
Вариант № 3. Однопараметрическое распределение Лапласа:
.
Исходные
данные:
Рассчитать аналитически: .
Найти точечную оценку параметра методом моментов.
Вариант № 4. Общее распределение Лапласа:
.
Исходные данные: a = 1.5, b = -2, = 0.005, = 0.94, n = 350.
Рассчитать аналитически: .
Найти точечные оценки параметров a и b методом моментов.
Вариант
№ 5. Распределение
Релея:
Исходные данные: a = 4, = 0.025, = 0.999, n = 375.
Рассчитать аналитически: .
Найти точечную оценку параметра a методом моментов.
Вариант № 6. Однопараметрическое логистическое распределение:
.
Исходные данные: a = 1/2, = 0.025, = 0.9, n = 400.
Рассчитать аналитически: .
Найти точечную оценку параметра a методом моментов.
Вариант № 7. Общее логистическое распределение:
.
Исходные данные: a = 1/2, b = 3, = 0.025, = 0.95, n = 350.
Рассчитать аналитически: .
Найти точечные оценки параметров a и b методом моментов.
Вариант № 8. Распределение Эрланга k-го порядка:
Исходные данные: a = 2, k = 3, = 0.025, = 0.9, n = 400.
Рассчитать
аналитически:
.
Найти точечные оценки параметров a и k методом моментов.
Указание: Воспользоваться тем, что моделируемая случайная величина
,
где
случайные величины
- независимы и распределены по
показательному закону с параметром a,
то есть:
,
.
Вариант № 9. Степенное распределение:
.
Исходные данные: a = 4, = 0.05, = 0.92, N = 300.
Рассчитать аналитически: .
Найти точечную оценку параметра a методом моментов.
Вариант № 10. Степенное распределение:
.
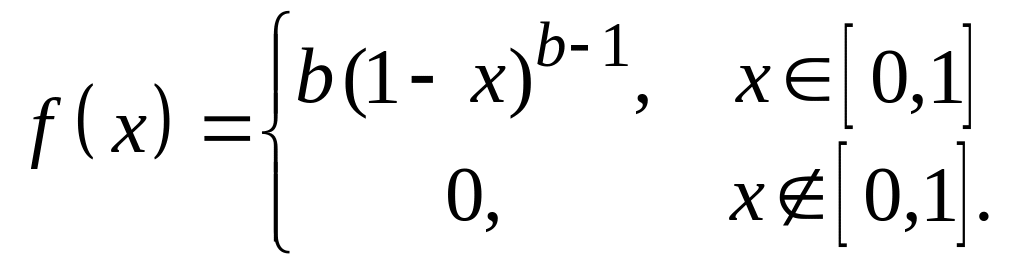Исходные данные: b = 5, = 0.05, = 0.92, N = 300.
Рассчитать аналитически: .
Найти точечную оценку параметра b методом моментов.
Вариант № 11. Однопараметрическое распределение прямоугольного треугольника:
Исходные данные: a = 0.5, = 0.1, = 0.98, n = 250.
Рассчитать аналитически: .
Найти точечную оценку параметра a методом моментов.
Вариант № 12. Однопараметрическое распределение прямоугольного треугольника:
Исходные данные: a = 3, = 0.1, = 0.98, n = 250.
Рассчитать аналитически: .
Найти точечную оценку параметра a методом моментов.
Вариант № 13. Общее распределение прямоугольного треугольника:
Исходные данные: a = -2, b= 3, = 0.01, = 0.95, n = 250.
Рассчитать аналитически: .
Найти точечные оценки параметров a и b методом моментов.
Вариант
№ 14.
Однопараметрическое распределение
Симпсона:
Исходные данные: a = 2, = 0.05, = 0.98, n = 300.
Рассчитать аналитически: .
Найти точечную оценку параметра a методом моментов.
Вариант № 15. Симметричное однопараметрическое распределение Симпсона:
Исходные данные: a = 2, = 0.05, = 0.95, n = 300.
Рассчитать аналитически: .
Найти точечную оценку параметра a методом моментов.
Вариант № 16. Общее распределение Симпсона:
Исходные данные: a = -0.8, b = 0.5, = 0.05, = 0.98, n = 300.
Рассчитать аналитически: .
Найти точечные оценки параметров a и b методом моментов.
Вариант
№ 17.
Исходные данные: a = 3, = 0.1, = 0.98, n = 350.
Рассчитать аналитически: .
Найти точечную оценку параметра a методом моментов.
Вариант
№ 18.
Исходные данные: a = 2, = 0.1, = 0.95, n = 350.
Рассчитать аналитически: .
Найти точечную оценку параметра a методом моментов.
Вариант
№ 19.
Исходные данные: a = 2, = 0.1, = 0.98, n = 250.
Рассчитать аналитически: .
Найти точечную оценку параметра a методом моментов.
Вариант
№ 20.
Исходные данные: a = 2, b = 10, = 0.1, = 0.98, n = 450.
Рассчитать аналитически: .
Найти точечные оценки параметров a и b методом моментов.
Вариант
№ 21.
.
Исходные данные: a = 2, b = -3, = 0.002, = 0.96, n = 350.
Считая
параметр a
известным,
рассчитать аналитически:
.
Найти точечную оценку параметра b
методом моментов.
Вариант № 22.
Исходные данные: a = 3, b = -3, = 0.002, = 0.98, n = 350.
Считая параметр b известным, рассчитать аналитически: . Найти точечную оценку параметра a методом моментов.
Вариант № 23. Распределение арксинуса:
Исходные данные: a = 1/2, = 0.025, = 0.94, n = 400.
Рассчитать аналитически: .
Найти точечную оценку параметра a методом моментов.
Вариант № 24.
Исходные данные: a = 2, b = 1, = 0.05, = 0.98, n = 400.
Рассчитать аналитически: .
Найти точечные оценки параметров a и b методом моментов.
Вариант № 25.
Исходные данные: a = 1.5, b = -1, = 0.01, = 0.98, n = 400.
Рассчитать аналитически: .
Найти точечные оценки параметров a и b методом моментов.
Вариант № 26.
Исходные данные: a = 1/2, = 0.01, = 0.96, n = 300.
Рассчитать аналитически: .
Найти точечную оценку параметра a методом моментов.
Вариант № 27.
Исходные данные: a = 1/2, = 0.001, = 0.95, n = 300.
Рассчитать аналитически: .
Найти точечную оценку параметра a методом моментов.
Вариант
№ 28. Гамма-распределение:
где
- гамма-функция.
Исходные данные: a = 2, = 3/2, = 0.01, = 0.99, n = 400.
Рассчитать аналитически: .
Найти точечные оценки параметров a и методом моментов.
Указание:
Воспользоваться алгоритмом моделирования
для случая, когда
или общим алгоритмом моделирования
гамма-распределения.
Вариант № 29. Общее бета-распределение:
Исходные данные: a = 2, b = 2, = 0.05, = 0.95, n = 300.
Рассчитать аналитически: .
Найти точечные оценки параметров a и b методом моментов.
Указание: Воспользоваться алгоритмом моделирования для случая целых a и b или общим алгоритмом моделирования бета-распределения.
Вариант № 30. Распределение Парето:
Исходные данные: a = 2, b = 2, = 0.05, = 0.92, n = 300.
Рассчитать аналитически: .
Найти точечные оценки параметров a и b методом моментов.
Указание:
Воспользоваться тем, что моделируемая
случайная величина
,
где
- случайная величина, имеющая
бета-распределение с параметрами a
и b
Исходные данные к разделу 3
Значения
параметров
заимствовать из раздела 1.
-
Вариант
aY
Вариант
aY
1
1.12
11.56
-0.21
16
2.35
7.5
0.24
2
-5.6
1.69
-0.15
17
-1.4
10.2
0.3
3
-3.3
4.7
0.74
18
3.7
4.41
-0.425
4
0.45
14.0
0.25
19
5.9
1.21
0.49
5
4.25
3.24
-0.33
20
2.2
6.25
0.045
6
-1.5
9.9
0.41
21
-2.35
8.0
-0.235
7
3.35
4.6
-0.29
22
-0.1
15.21
0.415
8
-5.4
1.75
0.12
23
2.4
8.5
-0.45
9
-4.5
3.61
-0.18
24
2.95
9.0
0.07
10
1.3
9.3
-0.63
25
-4.21
2.1
-0.39
11
4.48
2.56
0.08
26
5.25
1.44
0.14
12
0.5
10.7
-0.85
27
4.3
3.8
-0.54
13
-5.44
1.36
0.5
28
1.7
12.96
0.315
14
3.8
5.45
-0.37
29
-0.55
14.44
-0.125
15
-0.7
12.96
-0.05
30
-3.7
4.3
0.09
Приложение 2