Разложение непериодических колебаний. Интегральные преобразования фурье

Одиночный импульсu(t) также можно выразить рядом Фурье, мысленно представив его периодически повторяющимся с периодом T, большим или равным длительности импульса. Однако это будет верно лишь в интервале существования импульса u(t). В остальные моменты времени, когда заданный ряд, очевидно, будет периодически повторять u(t). Если необходимо получить аналитическое выражение импульсного непериодического колебания, верное в любой момент времени, следует использовать формы интегральных преобразований Фурье, которые можно вывести посредством предельного перехода при

Пусть задан импульс u(t) (рис.2.а). Сформируем периодическую последовательность f(t) таких импульсов (рис.2.б) с большим периодом Т. Тогда можно записать:

Для f(t) верно разложение в ряд Фурье (19) с коэффициентам, определяемыми по формуле (20). Интегрирование в (20) производится в пределах отрезка , где f(t) совпадает с u(t). Поэтому величина не изменится, если заменить f(t) на u(t) и интегрировать в бесконечных пределах:

Здесь величина

при произвольной частоте определяет спектральную плотность, спектральную функцию или спектральную характеристику импульса u(t).

Спектральная плотность не зависит от времени и является комплексной функцией частоты , существующей при положительных и при отрицательных значениях последней, причем, подобно (17), . Спектральная плотность однозначно определяется формой (аналитическим выражением) импульса u(t).

Формула (23) выражает прямое интегральное преобразование Фурье, которое символически можно записать так: .

Оно существует, если функция u(t)на любом отрезке конечной длины удовлетворяет условиям Дирихле и, кроме того, абсолютно интегрируема на бесконечном интервале, т. е.

Последнее всегда выполняется, если u(t) имеет конечную энергию, т. е. описывается функцией с интегрируемым квадратом.

Из (22) следует, что для вычисления комплексной амплитуды любой гармоники периодической последовательности импульсов достаточно вычислить спектральную плотность импульса u(t) образующего эту последовательность, взять значение функции на частоте искомой гармоники и умножить на 2/Т . Поэтому, учитывая, что , представим ряд (19) в форме:

Оценим, как изменится это равенство, если период сформированной последовательности беспредельно увеличивать. Тогда все импульсы кроме, исходного "отодвинутся" в бесконечность, и при конечных значениях tостанется только им пульс . Таким образом,

При величина определяющая основную частоту и расстояние между частотами соседних гармоник, стремится к чрезвычайно малой

, а сумма в пределе превращается в интеграл:

Эта формула позволяет осуществить обратное интегральное преобразование Фурье, т. е. вычислить значение импульса в любой момент времени, если известна его спектральная плотность. Пользуясь тем, что величины спектральной плотности при положительных и отрицательных значениях частоты комплексно сопряжены, выражение (24) можно записать в другой форме:

Где Re знак, значащий взятие действительной части.

Поэтому, представляя спектральную плотность в алгебраической форме

импульс , заданный только для , т.е. при , можно определить через действительную или мнимую составляющие.

Из рассмотренного следует, что интеграл Фурье (25) представляет непериодический импульс в виде бесконечной сумой гармонических составляющих с бесконечно малых амплитудами

и частотами , принимающими все значения от 0 до . Следовательно, непериодический импульс имеет непрерывный (сплошной) спектр. Причина этого — отсутствие однородности между и составляющими.

Преобразуя равенство Парсеваля (21) с учетом (22) и предельного перехода при от к , получим формулу Релея:

Итак, полная энергия непериодического колебания U(t) может быть вычислена по амплитудной спектральной характеристике

Ширина спектра является важным параметром колебания, необходимым при проектировании устройств передачи и обработки колебаний. На практике (размерность - герцы) определяется границей диапазона частот, в котором сосредоточена подавляющая часть (например, 90 %) энергии , т. е.

При осуществлении преобразований Фурье целесообразно использовать теоремы, устанавливающие их свойства и упрощающие вычисления. Приведем без доказательств некоторые из них.

Теорема наложения(суммирования)

Если ,то

Эта теорема справедлива для любого числа слагаемых.

Теорема пропорциональности

Если и A постоянная величина, то

Теорема смещения (запаздывания)

Если - отрезок времени, то

Следовательно, спектральная плотность импульса, возникшего на секунд позднее, равна спектральной плотности исходного импульса , умноженной на . Этот множитель изменяет только фазовые соотношения в спектре.

Существенное влияние на состав спектральной плотности ока­зывает симметрия импульса. Если четная функция (симметрия относительно оси ординат), т. е. , то спектральная плотность является чисто действительной функцией частоты. В случае, когда нечетная функция (симметрия относительно начала координат), т. е.

чисто мнимая функция.

Пример 2. Найти спектральную плотность экспоненциального импульса

где Е - амплитуда импульса;

параметр;

- момент "начала" импульса;

- вспомогательная единичная функция, обеспечивающая при всех , так как

Считают, что экспоненциальный импульс, представленный на рис.3.а в нормированном виде при , существует в пределах интервала , так как при "хвост" импульса меньше уровня 1%.

После подстановки в формулу (23), получаем при

Так как ,то спектральную плотность можно представить, в показательной форме:

Модуль и аргумент спектральной плотности импульса, т. е. амплитудная и фазовая спектральные характеристики, изображены сплошной и пунктирной кривыми на рис.3,б.

Последнее выражение можно использовать два нахождении по формуле (22) спектра периодической последовательности экспоненциальных импульсов, изображенной на рис.3.г для случая Амплитудно-частотный спектр последовательности приведен на рис.3.в, Этот спектр – дискретный, частоты соседних составлявших различаются на , а функция играет роль огибающей амплитуд спектра. Нетрудно проследить, как при увеличат периода (уменьшении ) составляющие спектра сближаются по частоте и уменьшается по амплитуде. В пределе (при и ) получится; сплошной спектр одиночного импульса с бесконечно малыми по амплитуде составляющими.

В заключение определим ширину спектра экспоненциального импульса, используя формулу (26). Полная энергия импульса равна:

Вычисление левой части формулы (26) не вызывает трудностей, так как, обозначив получаем табличный интеграл

После подстановки полученных выражений и в формулу (26) находим ширину спектра импульса .

Рис.З.Экспоненциальный импульс, его спектральная функции и амплитудный спектр периодической последовательности импульсов.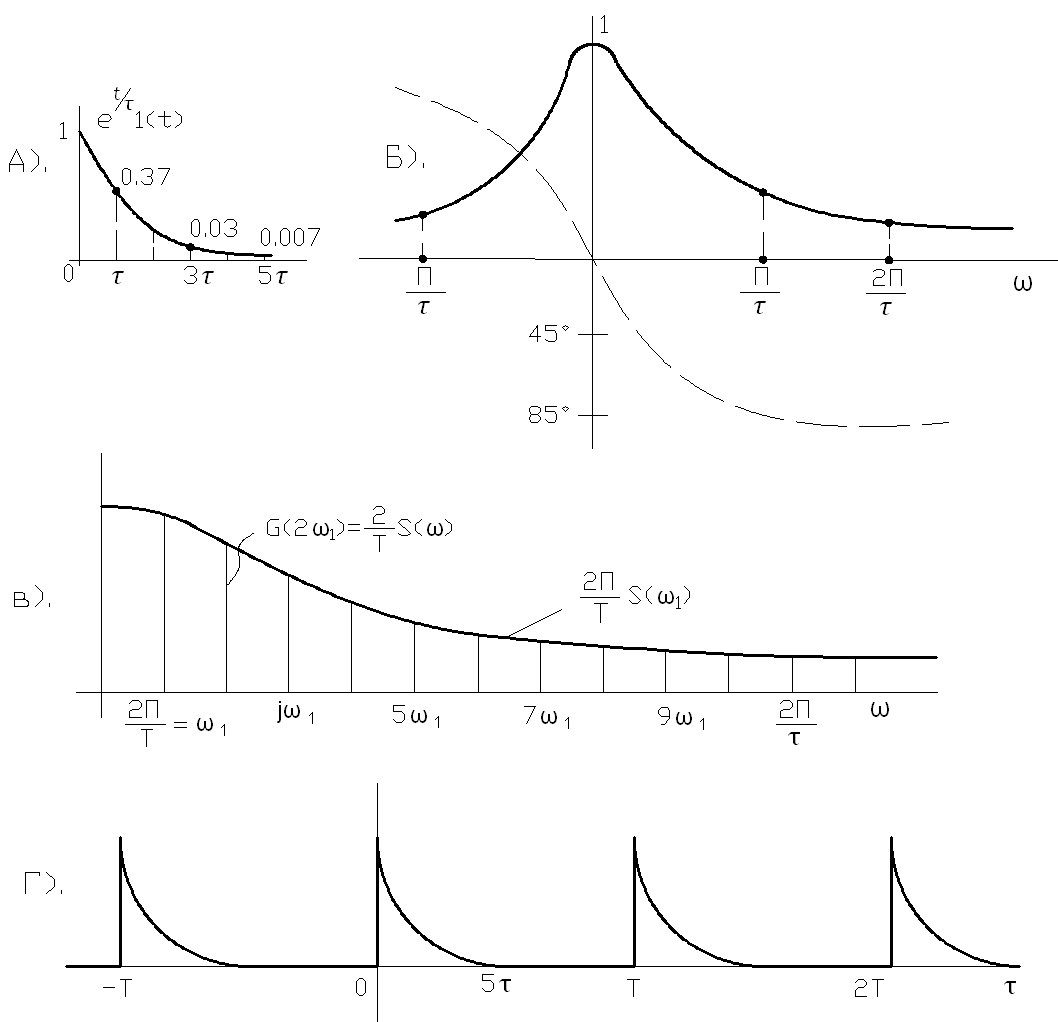

Рис.4

Таким образом чем короче импульс, тем шире его спектр.