2. Аппроксимация результатов измерения методом наименьших квадратов

Метод наименьших квадратов применяется в задачах выравнивания или сглаживания результатов измерений при выполнении, например, лабораторной работы по исследованию терморезисторов и других работ.

Пусть в результате измерений получен ряд точек с координатами (х₁, у₁), (х₂, у₂)… (х_n, у_n).

Если заранее известно, что зависимость между переменными линейного вида:

Y_T=a₀+a₁x, (2.1)

то необходимо определить коэффициенты a₀ и a₁, которые наилучшим образом описали бы зависимость, полученную при измерении. Наилучшее согласование достигается в случае, когда сумма квадратов отклонений опытных точек от точек, рассчитанных по теоретической кривой, обращается в минимум

, (2.2)

так как по условию Y_iT=a₀+a₁x, то

(2.3)

Функция S – функция двух независимых переменных a₀ и a₁, и для определения экстремума (максимума или минимума) функции нескольких переменных необходимо обращение в нуль ее частных производных первого порядка.

Вычислив частные производные функции S по a₀ и a₁ получим систему двух уравнений:

(2.4)

После преобразования получим:

(2.5)

Для определения a₀ и a₁ решаем систему двух уравнений с двумя неизвестными_. Известно, что решение системы уравнений, если оно существует, определяет значение параметров a₀ и a₁, минимизирующих S.

Пример 1. Описать линейной зависимостью соотношения между температурой и величиной сопротивления терморезистора

t0,C	40	50	60	80
R, Ом	15	20	24	35

При n=4 имеем:

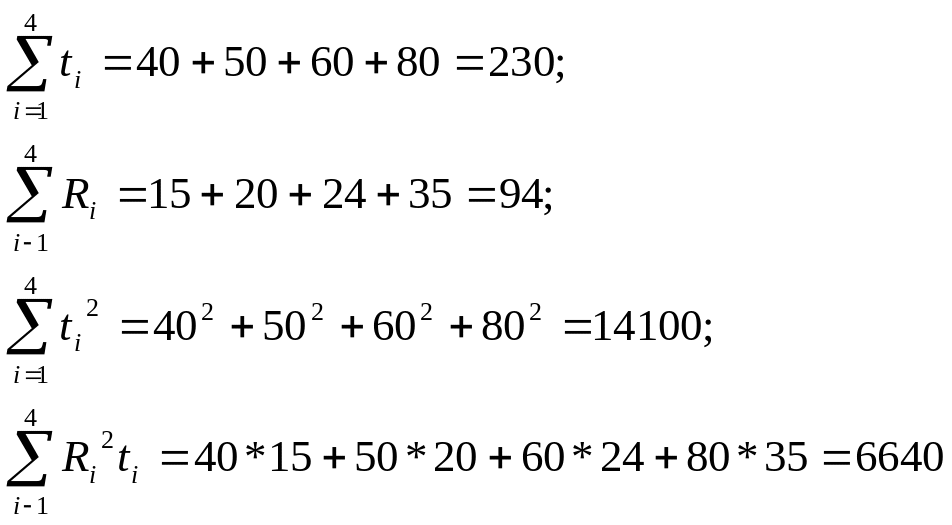
Составляем систему уравнений:

Решением системы является

а₀=-1,36 а₁=0,385

Тогда теоретическая зависимость сопротивления от температуры будет иметь вид

R_t=-1,36+0.385t

.

Метод наименьших квадратов применяется также для определения параметров нелинейной зависимости, например, квадратичной.

Пусть зависимость сопротивления от температуры описывается квадратичной зависимостью вида

R=at²+bt+c (2.6)

Необходимо определить параметры a, b и c, используя метод наименьших квадратов.

Подставим уравнение (2.6) в исходное выражение (2.2) и получим

(2.7.)

функцию трех независимых переменных a, b и c, по которым найдем частные производные первого порядка

(2.8)

Для составления системы уравнений по экспериментальным данным определим следующие коэффициенты:

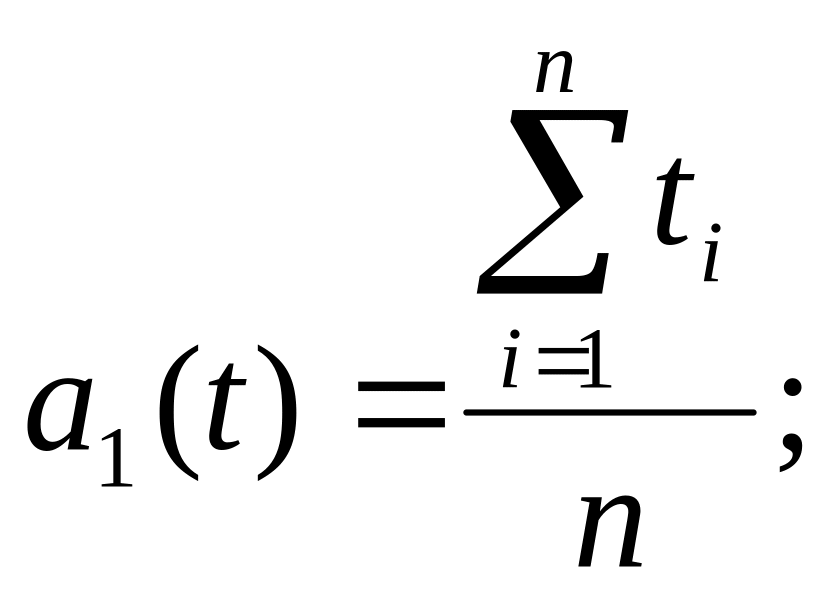
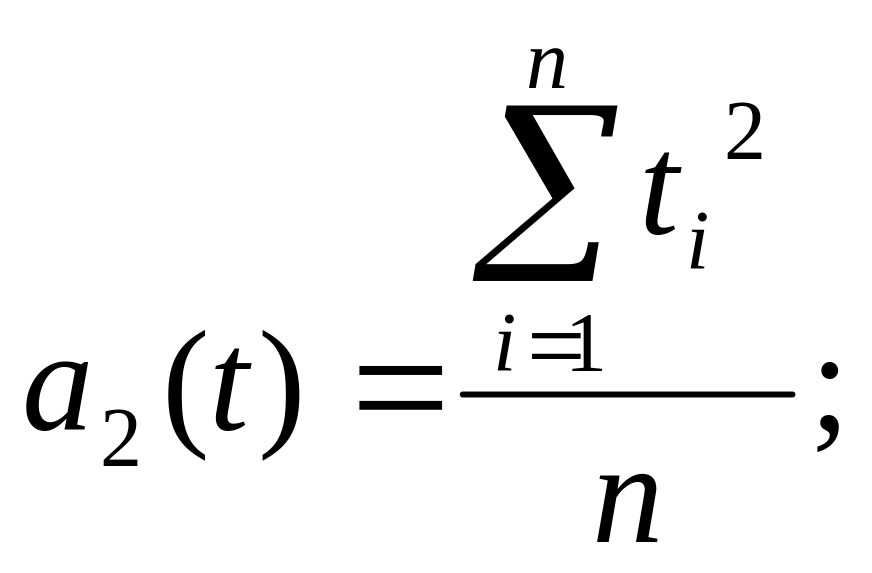
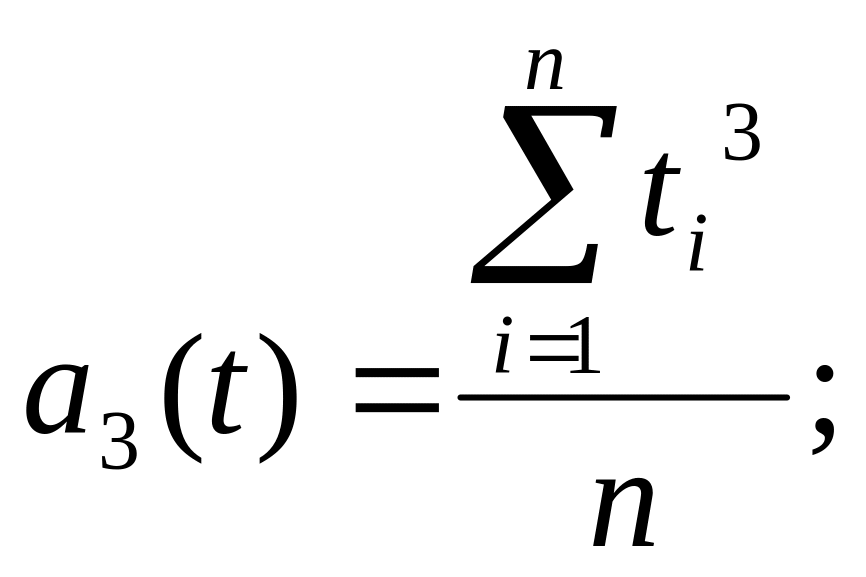
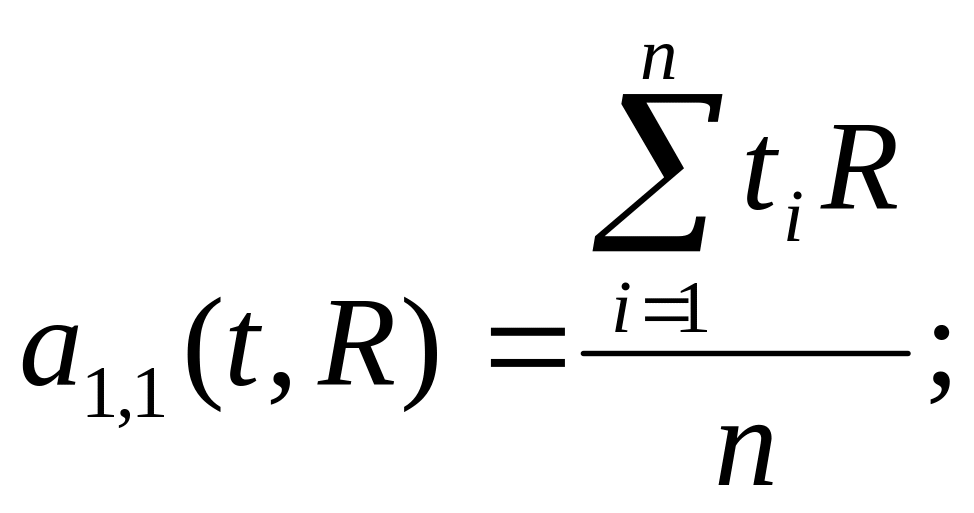
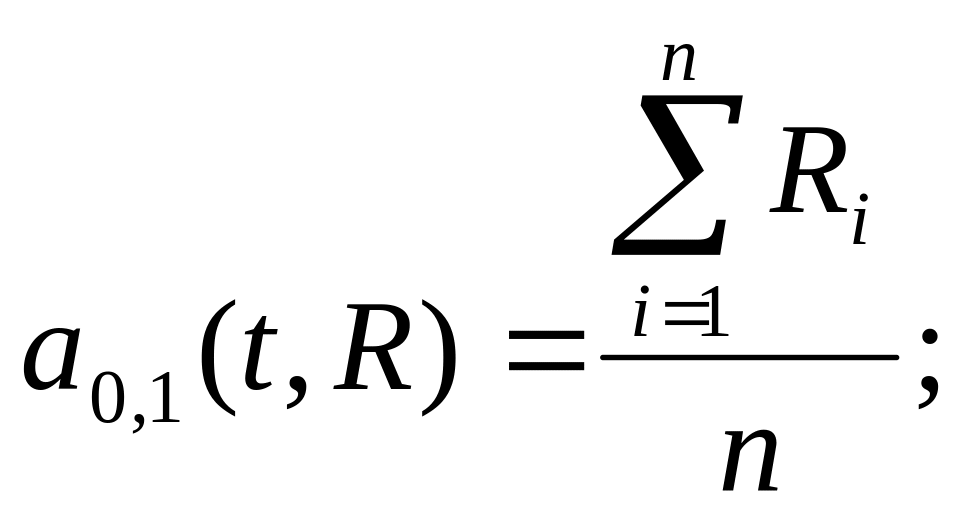
(2.9)

Система уравнений имеет вид:

(2.10)

Решая эту систему с помощью определителя или ЭВМ, находим численные значения коэффициентов a, b и c.

Для определения коэффициентов a, b и c составим определитель третьего порядка:

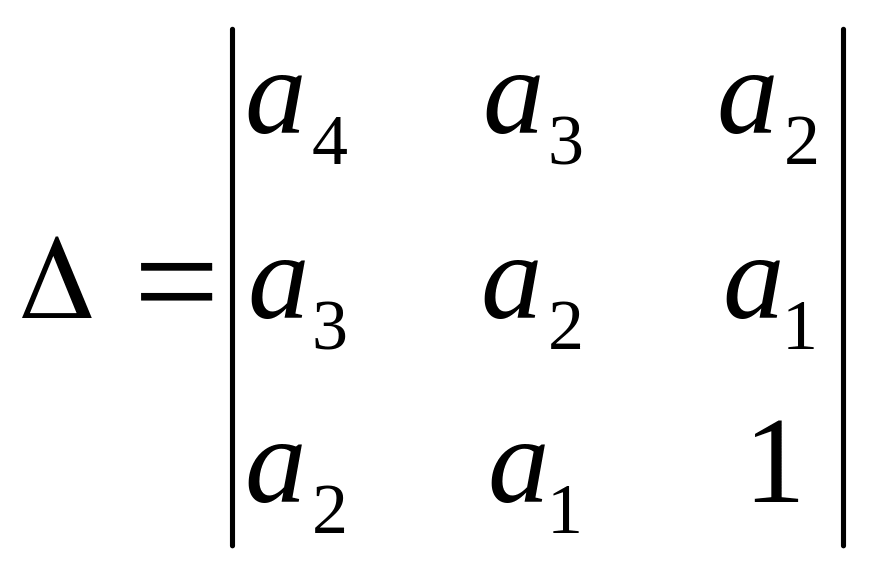
и алгебраические дополнения (миноры) элементов а₄, а₃ и а₂, заменяя соответственно элементы первого, второго, и третьего столбцов свободными членами

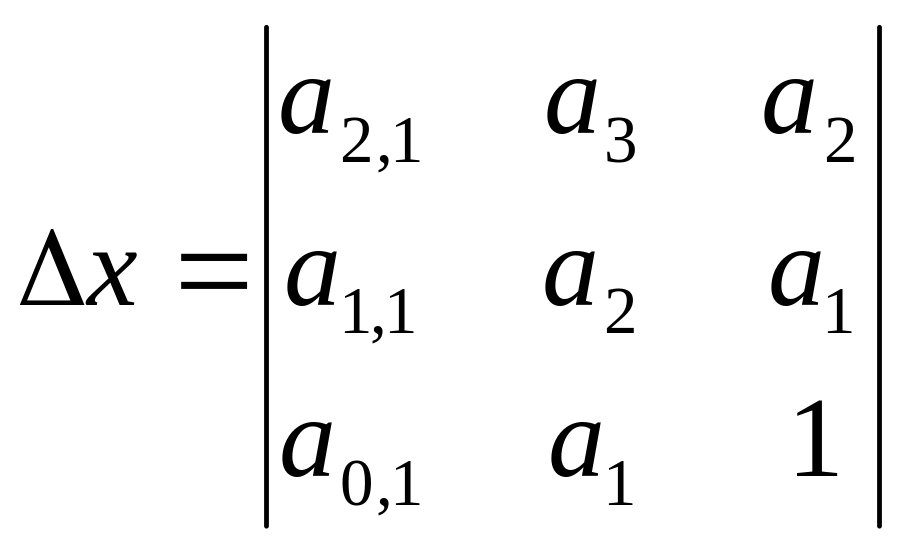
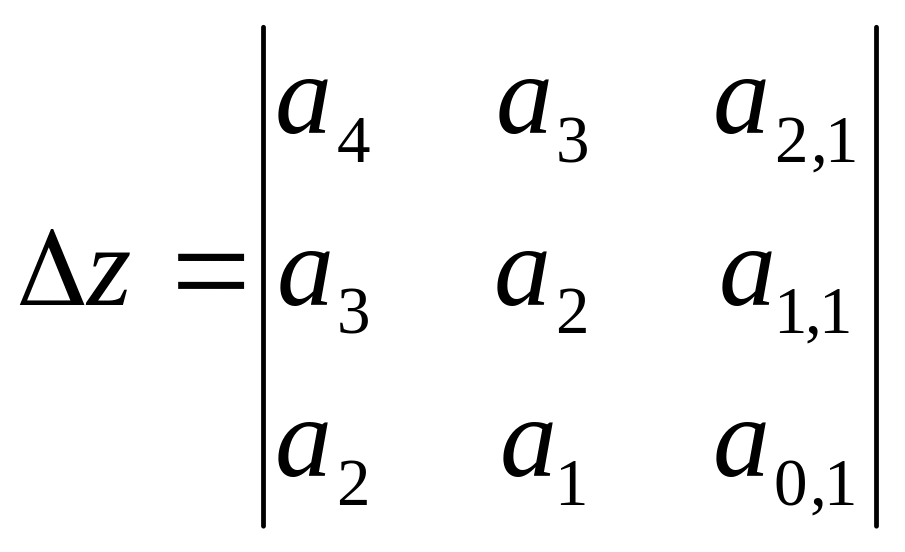
Если определитель системы не равен нулю 0, то система имеет единственное решение:

a=x/, b=y/, c=z/.

Определитель системы и соответствующие миноры определяются известным способом:

.

Для подтверждения совпадения теоретической и экспериментальной зависимостей сопротивления от температуры необходимо построить их график.

Задание №2

Описать линейной и нелинейной зависимостями соотношения между входной Х_i и выходной величиной У_i, используя метод наименьших квадратов,и построить теоретические и экспериментальные зависимости.