1. Обработка результатов измерений

При выполнении различных измерений необходимо оценить точность полученных результатов, т. е. определить погрешность измерений и вероятность их появления в определенных границах.

Наиболее достоверным значением измеряемой величины на основе ряда измерений является среднее арифметическое из полученных результатов измерений

,

где х_i – результат измерения, n – число измерений.

Разность между отдельными измерениями и средним арифметическим называется случайным отклонением результата измерения или остаточной погрешностью

(1.1)

Наиболее распространенной оценкой точности измерений является среднее квадратическое отклонение  результатов измерений, для нахождения которого необходимо знать закон распределения случайных погрешностей. В практике измерений наиболее распространен нормальный закон распределения случайных погрешностей (закон Гаусса), описываемый арифметическим выражением

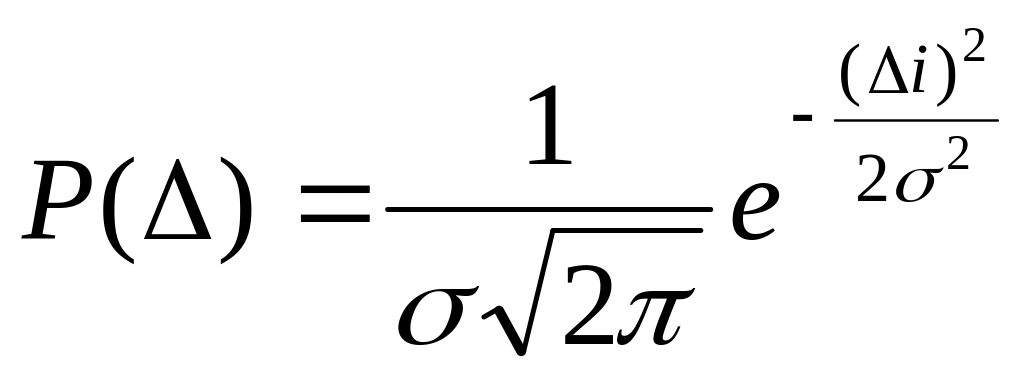, (1.2)

где

Р() – плотность вероятности случайной погрешности;

 - среднее квадратическое отклонение случайной погрешности.

Приближенно  может быть определено через остаточные погрешности.

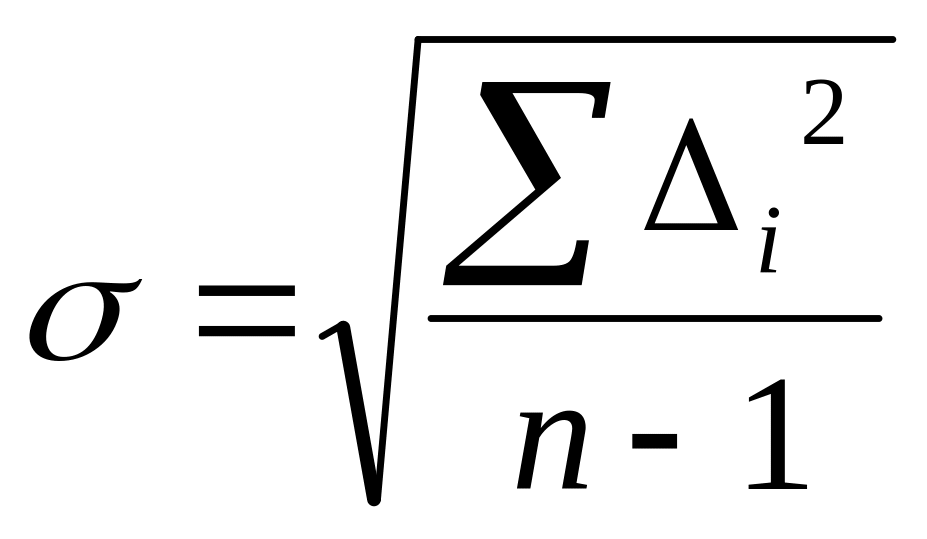(1.3)

Степень приближения среднего арифметического к истинному значению измеряемой величины характеризуется средней квадратической погрешностью _s среднего арифметического

,

Обычно при проведении измерений стремятся получить результат измерения с погрешностью, не превышающей допускаемое значение. Значение только среднего квадратического отклонения не позволяет найти максимальную погрешность, которая может встретиться при измерениях, что свидетельствует об ограниченных возможностях такой числовой характеристики погрешностей.

Максимальные значения погрешностей зависят не только от , но и от вида закона распределения. Когда распределение погрешности теоретически неограниченно, например, при нормальном законе распределения, погрешность может быть любой по значению.

В этом случае можно лишь говорить об интервале, за границы которого погрешность не выйдет с некоторой вероятностью. Этот интервал называют доверительным, характеризующую его вероятность – доверительной вероятностью, а границы этого интервала – доверительными значениями погрешности.

В практике измерений применяют различные значения доверительной вероятности, например: 0,90; 0,95; 0,98; 0,99; 0,9973; 0,999. Доверительный интервал и доверительную вероятность выбирают в зависимости от конкретных условий измерений.

Доверительная вероятность определяется из выражения

(1.4)

где

₂ - ₁ – доверительный интервал,

Р() – плотность вероятности случайной погрешности.

Оценка точности результатов измерений, основанная на нормальном законе распределения, применима к большому числу измерений (более 20).

В случае меньшего количества измерений, что часто имеет место на практике, задача определения доверительного интервала по заданной доверительной вероятности решается с помощью распределения Стьюдента, характер которого зависит от числа измерений.

В табл. 1.1 приведены значения коэффициентов t(n) этого распределения для разных величин доверительной вероятности Pg и числа измерений n.

Таблица 1.1