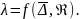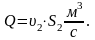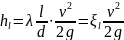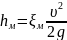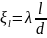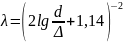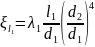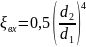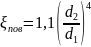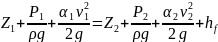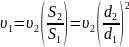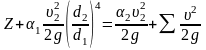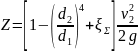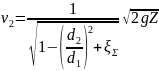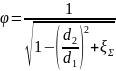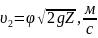- •1. Информация о дисциплине
- •1.1 Предисловие
- •1.2 Содержание дисциплины и виды учебной работы
- •1.2.1 Содержание дисциплины по гос
- •1.2.2 Объем дисциплины и виды учебной работы
- •Раздел 1
- •1.2 Статика жидкости и газа (10 часов)
- •1.3 Основы динамики жидкости и газа (10 часов)
- •1.4 Гидравлическое сопротивление и диссипация энергии потока вязкой жидкости (14 часов)
- •1.5 Гидравлический расчет трубопроводов и отверстий (12 часов)
- •1.6 Одномерные потоки газа (6 часов) (некоторые сведения из прикладной газовой динамики)
- •Раздел 2 Гидравлические объемные приводы (54 часа)
- •2.1 Общие сведения о гидроприводах (2 часа)
- •2.2 Объемные насосы и двигатели (10 часов)
- •2.3 Гидравлическая аппаратура управления (8 часов)
- •2.4 Вспомогательные устройства гидроприводов (8 часов)
- •2.5 Регулирование гидроприводов (10 часов)
- •2.6 Гидравлические следящие приводы (8 часов)
- •2.7 Основы проектирования и расчета гидроприводов (8 часов)
- •Раздел 3
- •2.2 Тематический план дисциплины для студентов заочной формы обучения
- •Раздел 3
- •Раздел 1
- •Раздел 2
- •2.4.2 Практические занятия для студентов заочной формы обучения
- •2.4.3 Лабораторные работы для студентов очно-заочной формы обучения
- •2.4.4 Лабораторные работы для студентов заочной формы обучения
- •2.5 Балльно-рейтинговая система
- •3.Информационные ресурсы дисциплины
- •3.1 Библиографический список
- •3.2 Опорный конспект Введение
- •Раздел 1 Теоретические основы Гидравлика
- •1.1 Физические свойства и энергонапряжённость жидкости и газа
- •Контрольные вопросы
- •1.2 Статика жидкостей и газов
- •Контрольные вопросы
- •1.3 Основы динамики жидкости и газа
- •Контрольные вопросы
- •1.4 Гидравлическое сопротивление и диссипация энергии потока вязкой жидкости
- •Контрольные вопросы
- •1.5 Гидравлический расчёт трубопроводов и отверстий
- •Контрольные вопросы
- •1.6 Одномерные потоки газа
- •Контрольные вопросы
- •Раздел 2 Гидравлические объемные приводы
- •2.1 Общие сведения о гидроприводах
- •Контрольные вопросы
- •2.2 Объемные насосы и гидродвигатели
- •Контрольные вопросы
- •2.3. Гидравлическая аппаратура управления
- •Контрольные вопросы
- •2.4 Вспомогательные устройства гидроприводов
- •Контрольные вопросы
- •2.5 Регулирование гидроприводов
- •Контрольные вопросы
- •2.6 Гидравлические следящие приводы
- •Контрольные вопросы
- •2.7 Основы проектирования и расчета гидроприводов
- •Контрольные вопросы
- •Раздел 3 Пневматические приводы
- •3.1. Общие сведения о пневмоприводах
- •Контрольные вопросы
- •3.2 Пневматические двигатели
- •Контрольные вопросы
- •3.3 Пневматическая аппаратура
- •Контрольные вопросы
- •3.4 Расчет пневмоприводов поступательного действия
- •Контрольные вопросы
- •3.3.1 Глоссарий-словарь терминов
- •3.3.2 Принятые обозначения на основе латинского алфавита
- •На основе греческого алфавита
- •Методические указания к решению задачи
- •Практическое занятие № 2 Расчет силового гидроцилиндра.Поступательного движения
- •Методические указания к решению задачи
- •3.5 Методические указания к выполнению лабораторных работ
- •3.5.1. Общие указания
- •Охрана труда и техника безопасности
- •III. Описание лабораторной установки
- •IV. Порядок выполнения работы
- •V. Содержание отчета
- •Вопросы для подготовки к защите отчета лабораторной работы
- •III. Описание лабораторной установки
- •IV. Порядок выполнения работы
- •V. Содержание отчета
- •Вопросы для подготовки к защите отчета лабораторной работы
- •III. Описание лабораторной установки
- •IV. Методика проведения работы
- •Энергетические испытания
- •Расчет технических параметров
- •V. Содержание отчета
- •Вопросы для подготовки к защите отчета лабораторной работы
- •III. Описание лабораторной установки
- •IV. Методика проведения работы
- •V. Содержание отчета
- •Вопросы для подготовки к защите отчета лабораторной работы
- •4. Блок контроля освоения дисциплины
- •4.1 Задания на контрольные работы и методические указания к их выполнению
- •Контрольная работа №1 задача 1 расчет напорной гидравлической системы
- •Методические указания к решению задачи 1
- •Задача 2 Определение давления в аккумуляторе в момент гидравлического удара
- •Методические указания к решению задачи
- •Методические указания к решению задачи 1
- •Задача 2 Расчет гидропривода поступательного движения с мультипликатором
- •Методические указания к решению задачи 2
- •4.2 Текущий контроль Тест №1
- •Тест №2
- •Раздел 3
- •Правильные ответы на тренировочные тесты текущего контроля
- •4.3 Итоговый контроль Вопросы к зачету
- •Содержание
- •1. Информация о дисциплине .3
Методические указания к решению задачи 1
Расход
воды Q
в системе определяется по величине
средней скорости
 потока в сечении трубопровода 3 и площади
сечения
потока в сечении трубопровода 3 и площади
сечения
|
|
((30)
|
Для определения средней скорости необходимо применить уравнение Бернулли для контрольных сечений 1-2 и 2-2 с учетом гидравлических потерь в трубопроводе.
Наметив плоскость сравнения 0-0, совпадающей с уровнем в баке 2, принять значения средних скоростей в контрольных сечениях равными нулю.
Гидравлические потери в трубопроводе состоят:
-из
потерь по длине в трубах 2 и 3 -
 ,
,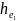 и
и 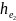
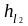 ;
;
-местных потерь:
-на
входе в трубопровод из бака 1-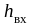 ;
;
-на
повороте трубопровода -
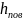 ,;
,;
-в
сужении трубопровода - 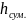
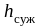 ;
;
-в
вентиле -
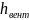
-на
выходе из трубопровода в бак 2 -

Выразив:
потери напора по длине по формуле Дарси
|
|
(31) |
местные по формуле Вессбаха
|
|
(32) |
составим
их сумму, вынося общий множитель
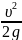 за скобки.
за скобки.
В
скобках получим коэффициент сопротивления
системы

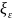 равный: сумме коэффициентов сопротивления
по длине
равный: сумме коэффициентов сопротивления
по длине
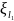 и
и

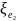 ,
коэффициентов местных сопротивлений:
на выходе из бака 1 -
,
коэффициентов местных сопротивлений:
на выходе из бака 1 -
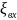 ,
на повороте трубопровода -
,
на повороте трубопровода -
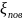 ,
на сужении трубопровода -
,
на сужении трубопровода -
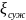
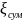 ,
в вентиле -
,
в вентиле -
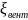 ,
на входе в бак 2 -
,
на входе в бак 2 -
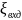 .
.
Коэффициенты
 ,
и
являются приведенными (к скорости
,
и
являются приведенными (к скорости
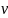 в трубе 3), т.е. умноженными на отношение
площадей сечения труб -
в трубе 3), т.е. умноженными на отношение
площадей сечения труб -
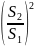 =
=
 .
.
Численные
значения коэффициентов местных
сопротивлений:
=0.5;
=1,1;
=0,5
[1-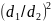 ];
];
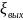 =1.
=1.
Коэффициент сопротивления по длине равен:
|
|
(33) |
где
гидравлический коэффициент трения
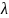 в первом приближении определяется по
формуле Прандтля – Никурадзе:
в первом приближении определяется по
формуле Прандтля – Никурадзе:
|
|
(34) |
причем эквивалентную шероховатость стенки можно считать равной 0,5 мм.
Порядок вычислений:
1.
Определяем коэффициенты гидравлического
трения
 и
и
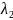 .
.
2. Вычисляем приведенные коэффициенты сопротивления:
|
|
(35) |
|
|
(36) |
|
|
(37) |
|
и . |
(38) |
3. Вычисляем коэффициент сопротивления системы :
|
|
(39) |
4. Записываем уравнение Бернулли в общем виде:
|
|
(40) |
В уравнении (40)
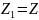 ;
;
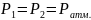 (атмосферное
давление);
(атмосферное
давление);
|
|
(41) |
(из условия неразрывности течения) ;
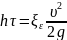
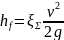 ,
- гидравлические потери.
,
- гидравлические потери.
Записываем уравнение Бернулли в преобразованном виде:
|
|
(42) |
Приняв
значения коэффициентов кинетической
энергии
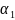 и
и
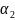 равными единице, решаем уравнение
равными единице, решаем уравнение
|
|
(43) |
Откуда
|
|
(44) |
Обозначим:- коэффициент скорости.
|
|
(45) |
Определим его численные значения и скорость
|
|
(46) |
По формуле определяется расход .
5. Проверка вычисленных значений коэффициентов и .
Коэффициенты и соответствуют так называемой квадратичной области сопротивления при турбулентном течении.
Здесь
эти коэффициенты зависят только от
относительной шероховатости стенки
трубы -
 .
Эта область находится на графике
зависимости λ=
.
Эта область находится на графике
зависимости λ=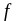 (
(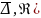 ,
приведенном в [2] в диапазоне Re
>
,
приведенном в [2] в диапазоне Re
>
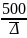 ,
где Re
- число Рейнольдса, определяемое по
формуле:
,
где Re
- число Рейнольдса, определяемое по
формуле:
|
|
(47) |
 Определив
по расходу и сечению трубы скорость и
рассчитав числа Рейнольдса
Определив
по расходу и сечению трубы скорость и
рассчитав числа Рейнольдса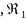 и,
и,
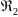 сопоставляем
эти числа с предельным значением Re>
Если полученные числа
сопоставляем
эти числа с предельным значением Re>
Если полученные числа
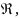 >
>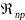 ,
то уточнений не требуется.
,
то уточнений не требуется.
В
противном случае надлежит вычислить
коэффициенты
и
по графику