1.6.6 Определение натяжений несущего троса при наибольших дополнительных нагрузках для

Наибольшими дополнительными нагрузками для контактной сети могут быть гололед с ветром и, ветер максимальной интенсивности. Для определения натяжения несущего троса, которое возникает при дополнительных нагрузках, воспользуемся уравнениями состояния в зависимости от исходного режима.

Определим натяжение несущего троса при гололеде с ветром :

(1.37)

, (1.38)

, (1.39)

. (1.40)

Входящее в выражение для определения и значение конструктивного коэффициента определяется по формуле (1.36) для .

При решении уравнений (1.37) воспользуемся методом линейной интерполяции и получим, что Н.

Проведем проверку:

,

Н,

Н/м,

,

^оС.

Проверка выполняется.

Определим натяжение несущего троса при ветре максимальной интенсивности :

. (1.41)

, (1.42)

, (1.43)

(1.44)

где - результирующая нагрузка на несущий трос при ветре максимальной интенсивности, Н/м.

Величина , входящая в формулы (1.43) и (1.44), определяется по выражению (1.36) для

При решении уравнений (1.41) воспользуемся методом линейной интерполяции и получим, что Н.

Проведем проверку:

,

Н,

Н/м,

,

^оС.

Проверка выполняется.

Значения Т_tгv и Т_tvmax наносятся на график Т_х=¦( t_х ), представленных на рисунке 1.3, в виде отдельных точек при сопутствующих температурах t_гv и t_vmax.

1.6.7 Определение стрел провеса несущего троса и контактного провода в зависимости от температуры для действительных пролетов

Вычисленные значения натяжения несущего троса для

будут соответствовать натяжениям троса для действительных пролетов, входящих в анкерный участок, но стрелы провеса несущего троса и контактного провода для различных длин пролета будут различными.

Расчет полукомпенсированной рессорной цепной подвески проводим для

длин пролета, равных l_min= 50 м, l_экв= 64 м, l_max= 70 м, для значений Т_х, изменяющегося в пределах от Т_мах до Т_min .

Стрелы провеса контактных проводов определяются по выражению:

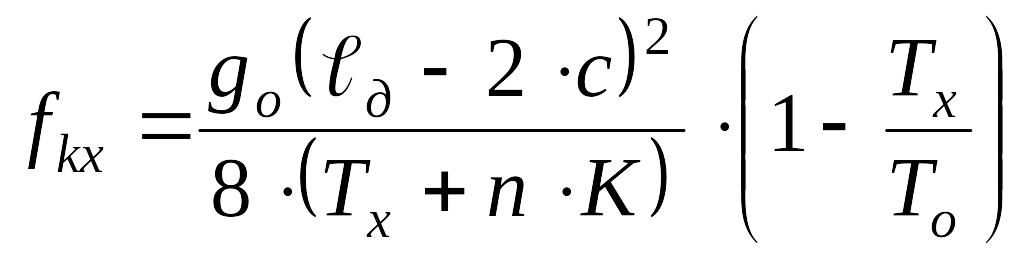, (1.45)

где - действительная длина пролета входящего в анкерный участок, м.

Стрела провеса несущего троса:

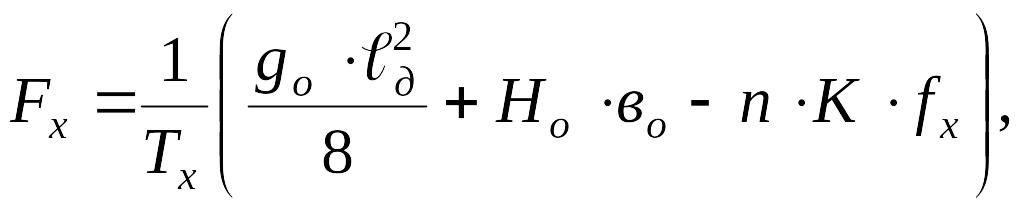(1.46)

где - натяжение рессорного троса, принимается равным 1500 Н;

- расстояние между несущим и рессорным тросами в опорном узле, м,

принимается равным м соответственно для длин пролетов от 40 до 70 м при одном контактном проводе в подвеске.

Результаты расчетов сводятся в таблицу 1.4 и отображаются на графике, представленном на рисунке 1.3.

Стрела провеса несущего троса при беспровесном положении контактного провода:

(1.47)

– для значения l_д1 = l_min : м;

– для значения l_д2 = l_экв : м;

– для значения l_д3 = l_max : м.