1.6.3 Определение температуры беспровесного положения контактного провода

Температуру беспровесного положения контактного провода можно

определить по формуле:

(1.27)

где и - соответственно максимальная и минимальная температуры, С⁰;

- при одиночных контактных проводах сечением 85 и 100 мм²_.

⁰С.

1.6.4 Определение точного значения натяжения несущего троса при беспровесном положении контактного провода То

Ранее использовалось приближенное значение . Для определения точного значения в соответствии с выбранным исходным режимом воспользуемся уравнением состояния:

. (1.28)

, (1.29)

(1.30)

, (1.31)

где - модуль упругости материала несущего троса, МПа;

- фактическая площадь сечения несущего троса, мм ;

- нагрузка от веса гололеда на цепную подвеску, Н/м.

Методом линейной интерполяции находим точное значение , соответствующее температуре :

,

,

Н/⁰С,

^оС.

1.6.5 Определение натяжения несущего троса в зависимости от температуры для эквивалентного пролета

Зависимость натяжения несущего троса от температуры определяется по уравнениям состояния:

. (1.32)

_(1.33)

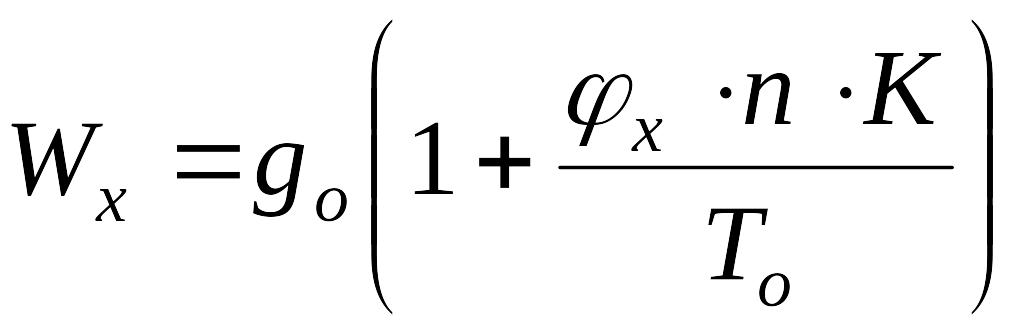, (1.34)

. (1.35)

Входящая в формулы (1.34) и (1.35) величина конструктивного коэффициента определяется по выражению:

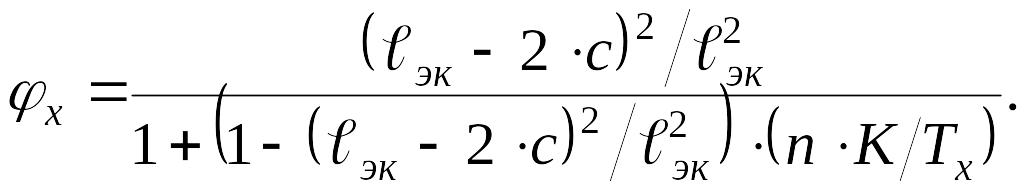_(1.36)

При решении уравнения (1.33) входящую в него величину , определяем с учетом точного значения полученного по формуле (1.28).

Задаваясь значениями с интервалами 500 или 1000 Н в диапазоне от до , находим соответствующие значения .

Приведем пример расчета для =19600 Н.

,

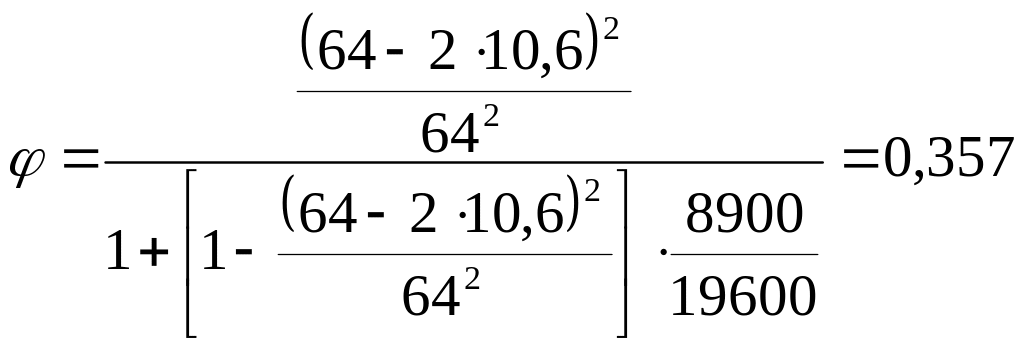Н/м,

Н,

,

⁰С.

Остальные рассчитанные значения сведены в таблицу 1.3.

Полученные результаты представляются в виде графика ,

представленного на рисунке 1.3.

Таблица 1.3 – Результаты расчетов

, Н	19600	18600	17600	16600	15600	14600	13600	12600	11600	10600	9900
	0,357	0,353	0,349	0,345	0,339	0,334	0,328	0,321	0,314	0,305	0,299
Н/м	24,94	24,88	24,83	24,77	24,69	24,63	24,55	24,45	24,36	24,24	24,15
, Н	22777	21742	20706	19670	18617	17573	16519	15457	14395	13315	12561
	6244	6214	6189	6160	6120	6090	6051	6001	5957	5899	5855
, 0С	-25	-29	-23	-17	-11	-4	3	11	19	28	40