5.4. Оцінювання рівномірності (нерівномірності) розподілу, подібності структур, структурних зрушень

Оцінка нерівномірності розподілу значень ознаки між окремими складовими сукупностей ґрунтується на порівнянні часток двох розподілів – за кількістю елементів сукупності d_j та за обсягом значень ознаки D_j. У випадку рівномірного розподілу значень ознаки d_j=D_j. Відхилення часток свідчить про певну нерівномірність розподілу, яка вимірюється коефіцієнтами:

- локалізації L_j = ;

- концентрації K =

Коефіцієнти локалізації обчислюються для кожної j-ї складової сукупності. У випадку рівномірного розподілу всі значення L_j=1. Якщо значення ознаки концентруються в j-й складовій, то L_j>1 і навпаки.

Коефіцієнт концентрації є узагальнюючою характеристикою відхилення розподілу від рівномірного. Його значення коливаються в межах від 0 до 1. У випадку рівномірного розподілу K=0. Чим помітніша концентрація, тим більше значення K відхиляється від 0.

Коефіцієнти концентрації та локалізації є ефективним засобом вимірювання диференціації сукупності за даними інтервальних рядів розподілу з нерівними інтервалами та за даними атрибутивних рядів.

Для порівняння структур двох об`єктів або одного об`єкта за двома ознаками визначають коефіцієнт подібності (схожості) структур P:

P = .

Чим більшими є відхилення структур, тим менше значення коефіцієнта P. Якщо структури однакові, то P=1.

Структура того чи іншого явища не залишається постійною ані у часі, ані у просторі. Структури однойменних явищ, що відносяться до різних просторових пунктів, підприємств тощо, як правило, не співпадають. Відмінності в структурі однойменних явищ (явищ, які порівнюються), визначаються різницею часток окремих частин сукупностей. Зміна часток окремих частин явища у часі свідчить про зміну структури, тобто структурні зрушення. Динамічний аналіз показників структури є дуже важливим для вивчення закономірностей розвитку економічних явищ у часі.

Інтенсивність структурних змін залежить від ступеню коливання показників абсолютних приростів і коефіцієнтів зростання часток окремих частин явища, що вивчається. В основу побудови узагальнюючих показників структурних зрушень покладено відповідні показники варіації.

Мірою інтенсивності структурних зрушень є середнє лінійне відхилення або середнє квадратичне відхилення часток, які називають коефіцієнтами структурних зрушень:

лінійний 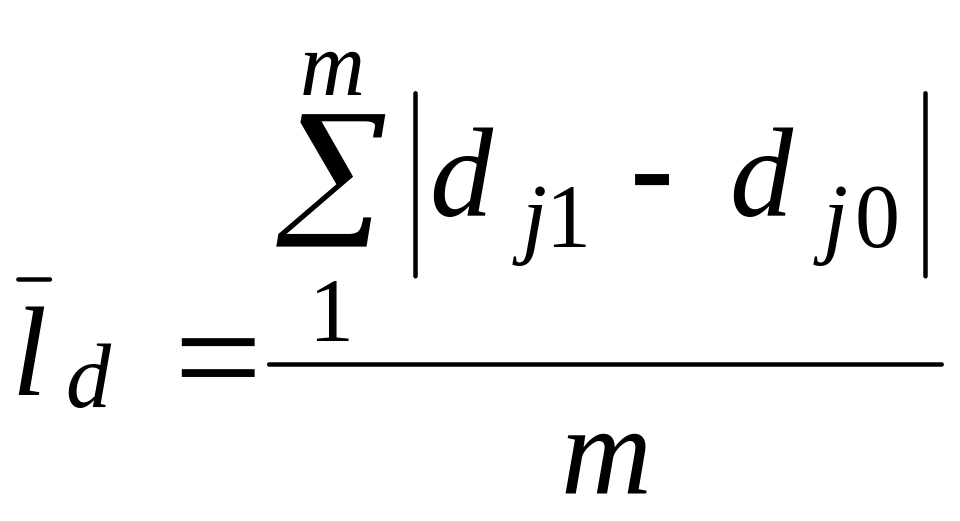; квадратичний ,

де m – кількість складових сукупності.

5.5. Правило складання (розкладання) дисперсій

При групуванні виникає варіація, зумовлена дією різних факторів, які впливають на варіацію ознаки в межах групи і між групами.

У структурованій сукупності, які поділена на групи за факторною ознакою x, дисперсія результативної ознаки y може бути розкладена на:

- дисперсію в кожній групі (внутрішньогрупову);

- дисперсію між групами (міжгрупову).

Загальна дисперсія характеризує варіацію ознаки y за рахунок впливу всіх причин (факторів).

Міжгрупова дисперсія характеризує результат впливу фактора x (групувального). Її обчислюють за формулою:

,

де та - це відповідно середня j-ї групи та загальна середня варіюючої ознаки y; - частота j-ї групи.

Внутрішньогрупові дисперсії розраховуються для кожної j-ї групи:

,

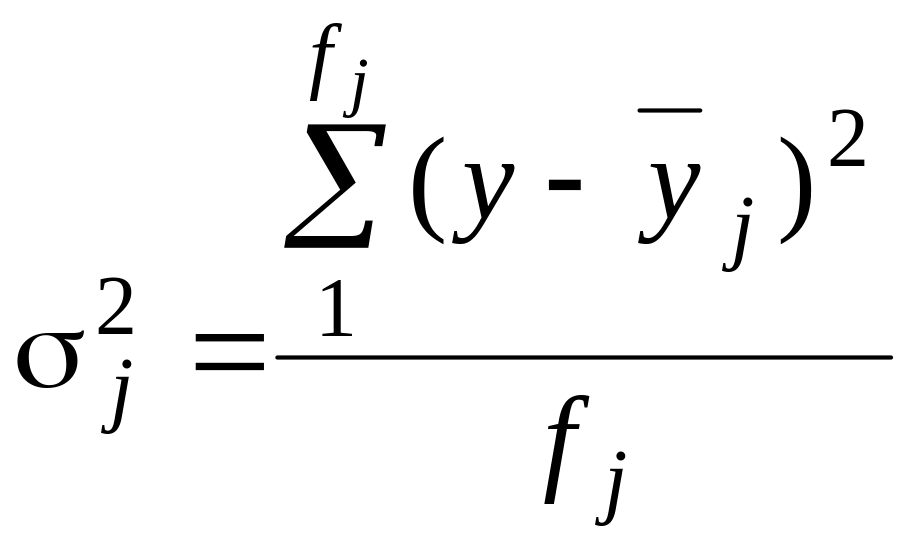де y – це значення ознаки окремих елементів сукупності.

В цілому для всіх груп визначають середню з внутрішньогрупових дисперсій, яка показує результат впливу інших факторів, що не враховані у групуванні (тобто всіх факторів, окрім фактора x). Для її розрахунку внутрішньогрупові дисперсії ( ) зважують на частоти відповідних груп ( ):

.

Взаємозв`язок між трьома дисперсіями називається правилом складання (розкладання) дисперсій:

,

тобто загальна дисперсія дорівнює сумі міжгрупової дисперсії і середньої з внутрішньогрупових дисперсій. Отже, знаючи дві будь-які дисперсії, на основі наведеної рівності завжди можна визначити третю.

Відношення міжгрупової дисперсії до загальної називається кореляційним відношенням [correlation ratio]:

.