17

Ряди розподілу. Аналіз варіацій та форми розподілу

5.1. Сутність та види рядів розподілу

5.2. Характеристики центру розподілу

5.3. Характеристики варіації

5.4. Оцінювання рівномірності (нерівномірності) розподілу, подібності структур, структурних зрушень

5.5. Правило складання (розкладання) дисперсій

5.1. Сутність та види рядів розподілу

Після оброблення та систематизації первинних статистичних матеріалів одержують ряди показників, які характеризують окремі аспекти явищ та процесів, що досліджуються. Такі статистичні ряди за своїм змістом поділяються на ряди розподілу та ряди динаміки.

Ряд розподілу характеризує склад, структуру сукупності за певною ознакою. Елементами ряду розподілу є варіанти x_j та частоти f_j. Варіантами називають окремі значення ознаки групування. Частоти показують, як часто зустрічаються в ряду розподілу ті чи інші варіанти.

Наприклад, маємо ряд розподілу студентів-заочників однієї групи за віком (табл.5.1):

Таблиця 5.1

Розподіл студентів за віком

Групи студентів за віком, років	До 20	20-25	25-30	30 і старші
Кількість студентів	8	10	4	2

В цьому випадку варіантами виступають значення віку студентів, а частотами – кількість студентів різних вікових груп.

Залежно від статистичної природи варіантів ряди розподілу поділяються на атрибутивні (в їх основу покладено якісні ознаки) та варіаційні (за ознаками, які мають кількісний вираз).

У співвідношенні варіантів і частот проявляється закономірність розподіл. Вона описується такими статистичними характеристиками як:

- частотні характеристики;

- характеристики центру розподілу;

- характеристики варіації;

- характеристики нерівномірності розподілу, концентрації, асиметрії.

Частотні характеристики – це абсолютна чисельність j-ї групи – частота f_j та відносна частота – частка d_j.

Додатковою характеристикою варіаційних рядів є кумулятивні (накопичені) частоти (частки ), які утворюються послідовним підсумовуванням абсолютних ( ) або відносних ( ) частот. Наведемо приклад визначення кумулятивних частот (табл.5.2).

Таблиця 5.2

Розподіл студентів за віком

Групи студентів за віком, років	xj	До 20	20-25	25-30	30 і старші	Разом
Кількість студентів	fj	8	10	4	2	24
Кумулятивні частоти		8	8+10=18	18+4=22	22+2=24	Х

Отже, = f₁ =8; =f₁+f₂=8+10=18; =f₁+f₂+f₃= + f₃=18+4=22; = f₁+f₂+f₃+f₄ = + f₄=22+2=24.

5.2. Характеристики центру розподілу

До характеристик центру розподілу відносять середню величину, моду та медіану. Середня величина характеризує типовий рівень ознаки в сукупності. За даними ряду розподілу середня визначається як середня арифметична зважена:

- на основі частот ;

- на основі часток ,

де m – число груп; x_j – середини інтервалів.

В інтервальних рядах розподілу, припускаючи рівномірний розподіл в межах j-го інтервалу, як варіант x_j використовують середину інтервалу. При цьому ширина відкритого інтервалу умовно вважається такою ж, як і найближчого закритого інтервалу. Так, перший інтервал (відкритий) умовно прирівнюється по ширині до другого (закритого), а останній (відкритий) - до передостаннього (закритого).

Найпоширеніше значення ознаки або значення ознаки, яке зустрічається в ряду розподілу найчастіше, називається модою (Mo).

В дискретних рядах розподілу моду визначають візуально, без додаткових розрахунків, як значення ознаки з найбільшою частотою (часткою). Найчастіше зустрічаються ряди розподілу з одним модальним значенням ознаки. Ряди, що мають дві моди, називаються бімодальними; ряди, що мають декілька мод – полімодальними.

Приклад. В новобудові пропонуються квартири з різною кількістю кімнат (табл.5.3):

Таблиця 5.3

Розподіл квартир в новобудові за кількістю кімнат

Кількість кімнат	1	2	3	4	5	Разом
У % до загальної кількості квартир	28,8	32,8	21,1	12,2	5,1	100,0

Визначимо модальне значення кількості кімнат в новобудові. Даний ряд розподілу є дискретним, отже моду визначають візуально. Найбільша частка квартир в новобудові (32,8%) – це 2-кімнатні квартири. Отже, Mo=2 кімнати. Таким чином, найчастіше в новобудові зустрічаються 2-кімнатні квартири.

В інтервальних рядах розподілу за найбільшою частотою (часткою) визначають спочатку модальний інтервал. В межах цього інтервалу знаходять значення так званої точкової моди:

Mo= ,

де x₀ – нижня межа модального інтервалу; h – його ширина;

f – частоти (частки): f_Mo-1 – передмодального інтервалу, f_Mo – модального інтервалу, f_Mo+1 – післямодального інтервалу.

Медіана (Me) – це варіанта, яка припадає на середину упорядкованого ряду розподілу і ділить його на дві рівні за обсягом частини – зі значеннями ознаки менше медіани і зі значеннями ознаки більше медіани.

Медіана не залежить від крайніх значень ознаки. Через це вона застосовується для характеристики центру в ряду розподілу з невизначеними межами. Для визначення медіани використовують кумулятивні (накопичені) частоти (частки).

Медіана ділить ряд розподілу навпіл, отже, в дискретному ряду розподілу вона знаходиться там, де накопичена частота складає половину або більше половини всієї суми частот, а попередня накопичена частота – менше половини обсягу сукупності.

В інтервальному варіаційному ряду таким чином визначається медіанний інтервал. А значення медіани обчислюється за формулою:

Me= ,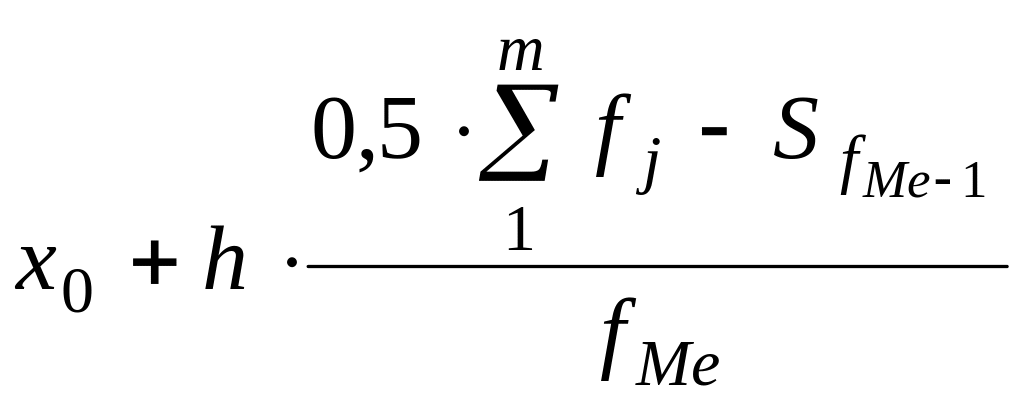

де x₀ та h – це нижня межа та ширина медіанного інтервалу;

- частота медіанного інтервалу; - кумулятивна частота передмедіанного інтервалу.

Якщо значення середньої величини, моди і медіани співпадають ( ), то даний ряд розподілу є симетричним. Для правосторонньої асиметрії ; для лівосторонньої - . Для помірно асиметричних розподілів справедливою є рівність: .

Кількісні зміни значень ознаки при переході від однієї одиниці сукупності до іншої називаються варіацією. Чим меншою є варіація, тим більш надійними й типовими є характеристики центру розподілу, насамперед, середня величина.