1.1Нули передаточной функции это …

только неустойчивые корни числителя

корни числителя

корни знаменателя

только неустойчивые корни знаменателя

1.2 Дифференциальным уравнением соответствующим передаточной функции вида:

является …

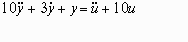
1.3 Для построения амплитудно-частотной характеристики необходимо найти …

ВАРИАНТЫ ОТВЕТОВ: 1)  амплитуду и фазу выходного сигнала    2)  амплитуду выходного сигнала 3)  модуль частотной передаточной функции    4)  аргумент  частотной передаточной функции

1.4 Наклон асимптотической ЛАЧХ на частоте 25 1/с звена с передаточной функцией вида:

равен ______ дБ/дек.

40

0

20

-20

2.5 Установите соответствие между видом дифференциального уравнения и названием типового динамического звена

1.

2.

3.

4.

консервативное звено

апериодическое звено первого порядка

апериодическое звено второго порядка

дифференцирующее звено

2.6 Переходная функция звена с передаточной функцией

2.7Аналитическое выражение для мнимой части частотной передаточной функции апериодического звена 1-го порядка имеет вид …

2.8 При параллельном соединении двух звеньев с передаточными функциями H(s)=2/s и H(s)=3/(s+1) результирующая передаточная функция будет иметь вид

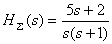
3.9 Устойчивость линейной динамической системы может быть определена по характеру …

свободного движения

вынужденного движения

установившегося движения

возмущенного движения

3.10 Матрица Гурвица М для системы:

равна …

3.11 Замкнутая система с передаточной функцией разомкнутого контура

будет устойчива при значении К …

2<K<4

K>0,75

K<0,75

K=0,75

3.12 Логарифическая амплитудно-фазо-частотная характеристика системы приведена на рисунке.

Запас устойчивости по фазе данной системы равен …

90°

180°

60,5°

119,5°

4.13 При заданных гармоническом входном воздействии амплитудой G и частотой ω_к, и допустимой ошибке системы е_доп, ордината контрольной точки низкочастотного участка логарифмическая амплитудная характеристика определяется, как …

20 lg( G )

20 lg(G/ е_доп )

20 lg( е_доп / G )

20 lg( е_доп )

4.14 Увеличение протяженности среднечастотной части логарифмической амплитудной характеристики с наклоном – 20 дБ/декаду …

приводит к увеличению запаса устойчивости по фазе

приводит к уменьшению запаса устойчивости по фазе

не влияет на запас устойчивости по фазе

делает его равным π

4.15 ЛАХ последовательного корректирующего L_кз звена вычисляется по располагаемой L_р и желаемой L_ж логарифмической амплитудной характеристики системы, как …

L_кз = L_ж * L_р

L_кз = L_р + L_ж

L_кз = L_ж / L_р

L_кз = L_ж - L_р

4.16 Для увеличения запаса устойчивости по фазе при последовательной коррекции может быть применено ______________ звено.

безынерционное

интегрирующее

дифференцирующее

апериодическое первого порядка.

4.17 Значение фазовой характеристики разомкнутой системы с передаточной функцией W(s) = 100/s(0,1s+1) на частоте ω=10 1/c равно …

-3π/4

-π/4

-2π/3

-π

4.18 Логарифмическая амплитудная характеристика разомкнутой системы с передаточной функцией W(s) = 100/s(0,1s+1)(0,5s+1) на частоте ω = 1 1/c имеет наклон _________ дБ/декаду.

-20

0

-40

-60

1.1Передаточная функция это …

отношение изображения Лапласа выходного сигнала к изображению Лапласа входного сигнала, вычисленное при нулевых начальных условиях

отношение выходного сигнала к входному сигналу

отношение изображения Лапласа входного сигнала к изображению Лапласа выходного сигнала, вычисленное при нулевых начальных условиях

отношение амплитуды выходного сигнала к амплитуде входного сигнала

1.2Дифференциальным уравнением соответствующим передаточной функции вида:

является …

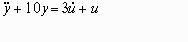
1.3Для построения амплитудно-частотной характеристики необходимо найти …

ВАРИАНТЫ ОТВЕТОВ: 1)  амплитуду и фазу выходного сигнала    2)  амплитуду выходного сигнала 3)  модуль частотной передаточной функции    4)  аргумент  частотной передаточной функции

1.4 Наклон ЛАЧХ, соответствующей передаточной функции вида

на частоте =150[1/c] равен ______ дБ/дек.

-40

0

20

-20

2.5 Установите соответствие между видом дифференциального уравнения и названием типового динамического звена

1.

2.

3.

4.

апериодическое звено первого порядка.

реальное дифференцирующее звено.

дифференцирующее звено.

интегрирующее звено

2.6 Реакцией звена с передаточной функцией 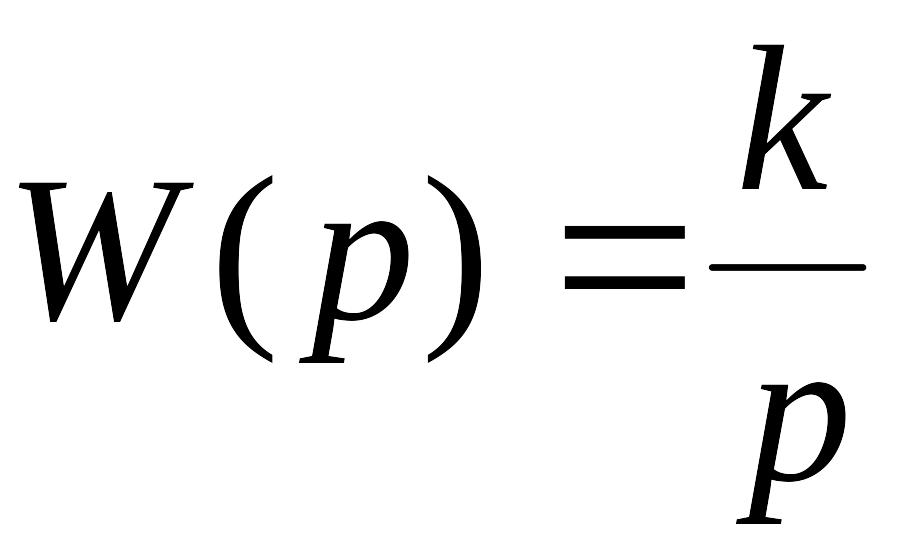на единичное ступенчатое входное воздействие является …

линейно нарастающий сигнал

затухающие гармонические колебания

экспонента

гармонические колебания постоянной амплитуды

2.7 Постоянная времени звена, переходная функция которого представлена на следующем рисунке:

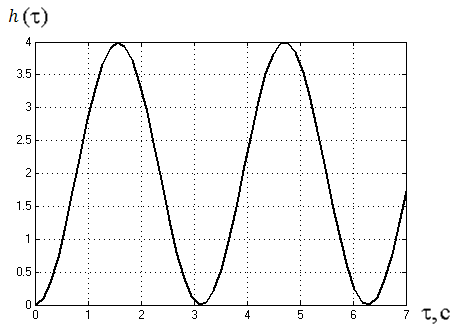
равен:

2.8 Если H1(s)=2 - передаточная функция прямой связи, а H2(s)=1/s+1 - передаточная функция отрицательной обратной связи, то результирующая передаточная функция будет определяться выражением …

3.9 Переходная составляющая решения дифференциального уравнения, описывающего поведение линейной системы, имеет вид

у_п(t) = C₁exp(α₁t) + C₂exp(α₂t) +...+ C_kexp(α_kt),

где: С_i, α_i - вещественные числа, i = 1...k; t - время. Необходимым и достаточным условием устойчивости такой системы является условие

|α_i| <1, i = 0,...,k

α_i<0, i = 0,...,k

C_i<0, i = 0,...,k

|C_i| <1, i = 0,...,k

3.10 Для устойчивости системы с характеристическим полиномом

D(p) = T₁T₂p³ + (T₁+T₂)p² + p + K

при положительных значениях параметров T₁ , T₂ и К, необходимо и достаточно выполнение условия …

T₁ + T₂ - T₁ T₂ > 0

K T₁ T₂ - T₁ - T₂ > 0

T₁ + T₂ - K T₁ T₂ > 0

К - T₁ T₂ > 0

3.11 Границы устойчивости для замкнутой системы, заданной передаточной функцией разомкнутой системы вида

,

может быть задана уравнением …

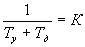
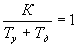
3.12 Логарифическая амплитудно-фазо-частотная характеристика системы приведена на рисунке.

Запас устойчивости по фазе данной системы …

86°

Отсутствует, система неустойчива

176°

4°

4.13 При заданных гармоническом входном воздействии амплитудой G и частотой ω_к, и допустимой ошибке системы е_доп, абсцисса контрольной точки низкочастотного участка логарифмической амплитудной характеристики равна …

20 lg(ω_к)

lg(ω_к / е_доп)

lg(1) = 0

lg(ω_к)

4.14 Увеличение протяженности среднечастотной части логарифмической амплитудной характеристики с наклоном – 20 дБ/декаду …

приводит к увеличению запаса устойчивости по фазе

приводит к уменьшению запаса устойчивости по фазе

не влияет на запас устойчивости по фазе

делает его равным π

4.15 На рисунке показаны логарифмические амплитудные характеристики для двух систем. Система 2 будет …

иметь больше запас устойчивости по фазе

более точной при отработке постоянных по величине воздействий

более быстродействующей

более точной при отработке линейно изменяющихся воздействий

4.16 Фазовая характеристика разомкнутой системы с передаточной функцией W(s) = 100/s(0,1s+1)(s+1) при увеличении частоты ω→ стремится к асимптоте …

-π/4

-2π/3

-3π/2

-π

4.17Логарифмическая амплитудная характеристика разомкнутой системы с передаточной функцией W(s) = 100/s(0,1s+1)(0,5s+1) на частоте ω = 1 1/c имеет наклон _________ дБ/декаду.

-20

0

-40

-60