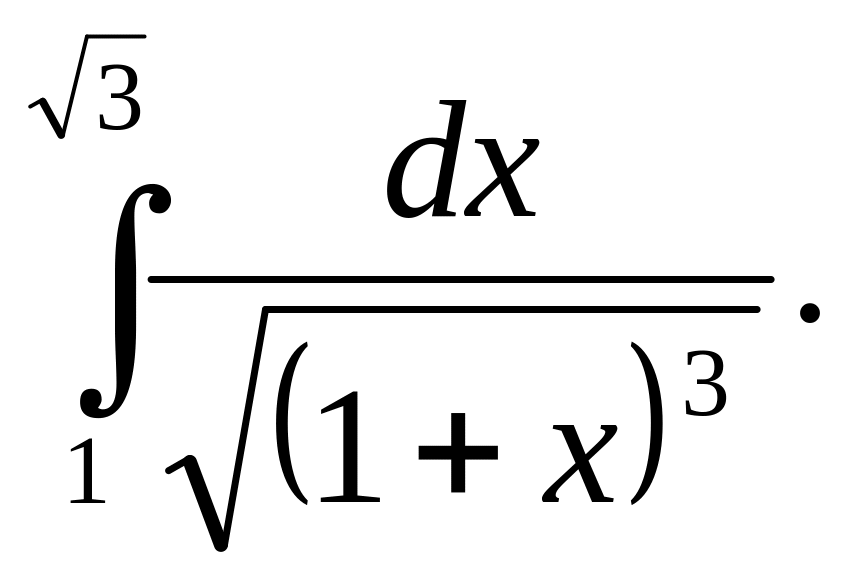- •17. Изменить порядок интегрирования в двойном интеграле:
- •17. Изменить порядок интегрирования в двойном интеграле:
- •19. Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями: .
- •21. Найти общее решение дифференциального уравнения:
- •17. Изменить порядок интегрирования в двойном интеграле:
- •19. Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями: .
- •21. Найти общее решение дифференциального уравнения:
- •17. Изменить порядок интегрирования в двойном интеграле:
- •19. Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями: .
- •21. Найти общее решение дифференциального уравнения:
- •17. Изменить порядок интегрирования в двойном интеграле:
- •19. Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями: .
- •21. . Найти общее решение дифференциального уравнения:
- •17. Изменить порядок интегрирования в двойном интеграле:
- •19. Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями: .
- •21. Найти общее решение дифференциального уравнения:
- •17. Изменить порядок интегрирования в двойном интеграле:
- •19. Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями: .
- •21. Найти общее решение дифференциального уравнения:
- •17. Изменить порядок интегрирования в двойном интеграле:
- •19. Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями: .
- •21. Найти общее решение дифференциального уравнения:
- •17. Изменить порядок интегрирования в двойном интеграле:
- •19. Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями: .
- •21. Найти общее решение дифференциального уравнения:
- •17. Изменить порядок интегрирования в двойном интеграле:
- •21. Найти общее решение дифференциального уравнения:
- •17. Изменить порядок интегрирования в двойном интеграле:
- •19. Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями: .
- •21. Найти общее решение дифференциального уравнения:
- •17. Изменить порядок интегрирования в двойном интеграле:
- •19. Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями: .
- •21. Найти общее решение дифференциального уравнения:
- •17. Изменить порядок интегрирования в двойном интеграле:
- •19. Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями: .
- •21. Найти общее решение дифференциального уравнения:
- •17. Изменить порядок интегрирования в двойном интеграле:
- •21. Найти общее решение дифференциального уравнения:
- •17. Изменить порядок интегрирования в двойном интеграле:
- •21. Найти общее решение дифференциального уравнения:
- •17. Изменить порядок интегрирования в двойном интеграле:
- •21. Найти общее решение дифференциального уравнения:
- •17. Изменить порядок интегрирования в двойном интеграле:
- •19. Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями: .
- •21. Найти общее решение дифференциального уравнения:
- •17. Изменить порядок интегрирования в двойном интеграле:
- •19. Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями: .
- •21. Найти общее решение дифференциального уравнения:
- •17. Изменить порядок интегрирования в двойном интеграле:
- •19. Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями: .
- •21. Найти общее решение дифференциального уравнения:
- •17. Изменить порядок интегрирования в двойном интеграле:
- •19. Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями: .
- •21. Найти общее решение дифференциального уравнения:
- •17. Изменить порядок интегрирования в двойном интеграле:
- •19. Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями: .
- •21. Найти общее решение дифференциального уравнения:
- •17. Изменить порядок интегрирования в двойном интеграле:
- •19. Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями: .
- •21. Найти общее решение дифференциального уравнения:
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА № 2
для студентов 1 курса ДО
филиала ФГБОУ ВПО УГАТУ в г. Стерлитамаке
специальностей: 150700.62 - «Машиностроение», 151900.62 – «Конструкторско-технологическое обеспечение машиностроительных производств»,
221000.62 - «Мехатроника и робототехника»
2семестр
Темы: «Интегральное исчисление», «Кратные интегралы»
«Дифференциальные уравнения»
Составитель: к ф.-м. н. Г.Ф. Ефимова
Вариант – 1
Найти интегралы:
1.
2.
3.
4.
5.
|
6.
7.
8.
9.
10.
|
Вычислить несобственные интегралы или доказать их расходимость:
11.
|
12.
|
Найти площадь фигуры, ограниченной линиями:
13.
|
14.
|
Вычислить длину дуги, заданной уравнением:
15.
|
16.
|
17. Изменить порядок интегрирования в
двойном интеграле:
![]()
18. Вычислить площадь части поверхности
![]() ,
лежащей в I октанте.
,
лежащей в I октанте.
19. Вычислить с помощью тройного интеграла
объем тела, ограниченного указанными
поверхностями:
![]() .
.
20. Найти координаты центра тяжести
однородного тела, ограниченного
параболоидом
![]() и плоскостью
и плоскостью
![]() .
.
21. Найти общее решение дифференциального уравнения:
1)
![]() ;
;
2)
![]() .
.
Вариант – 2
Найти интегралы:
1.
2.
3.
4.
5.
|
6.
7.
8.
9.
10.
|
Вычислить несобственные интегралы или доказать их расходимость:
11.
|
12.
|
Найти площадь фигуры, ограниченной линиями:
13.
|
14.
|
Вычислить длину дуги, заданной уравнением:
15.
|
16.
|
17. Изменить порядок интегрирования в двойном интеграле:
18. Вычислить площадь части поверхности
![]() ,
отсеченной плоскостями
,
отсеченной плоскостями
![]() .
.
19. Тело ограничено параболоидом
![]() и сферой
и сферой
![]() .
Вычислить его объем, внутренний по
отношению к параболоиду.
.
Вычислить его объем, внутренний по
отношению к параболоиду.
20. Найти момент инерции однородного шара (плотность равна 1) радиуса 2 относительно его центра.
21. Найти общее решение дифференциального уравнения:
1)
![]() ;
;
2)
![]() .
.
Вариант – 3
Найти интегралы:
1.
2.
3.
4.
5.
|
6.
7.
8.
9.
10.
|
Вычислить несобственные интегралы или доказать их расходимость:
11.
|
12.
|
Найти площадь фигуры, ограниченной линиями:
13.
|
14.
|
Вычислить длину дуги, заданной уравнениями:
15.
|
16.
|
17. Изменить порядок интегрирования в двойном интеграле:
18. Вычислить площадь части поверхности
полусферы![]() ,
вырезанной цилиндром
,
вырезанной цилиндром
![]() .
.
19. Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями: .
20. Найти массу куба
![]() ,
если плотность его в каждой точке
,
если плотность его в каждой точке
![]() равна
равна
![]() .
.
21. Найти общее решение дифференциального уравнения:
1)
![]() ;
;
2)
![]() .
.
Вариант – 4
Найти интегралы:
1.
2.
3.
4.
5.
|
6.
7.
8.
9.
10.
|
Вычислить несобственные интегралы или доказать их расходимость:
11.
|
12.
|
Найти площадь фигуры, ограниченной линиями:
13.
|
14.
|
Вычислить длину дуги, заданной уравнением:
15.
|
16.
|
17. Изменить порядок интегрирования в двойном интеграле:
18. Найти площадь части плоскости
![]() ,
заключенной между координатными
плоскостями.
,
заключенной между координатными
плоскостями.
19. Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями: .
20. Найти массу тела, ограниченного
цилиндрической поверхностью
![]() и плоскостями
и плоскостями
![]() ,
если в каждой его точке плотность
численно равна ординате этой точки.
,
если в каждой его точке плотность
численно равна ординате этой точки.
21. Найти общее решение дифференциального уравнения:
1)
![]() ;
;
2)
![]() .
.
Вариант – 5
Найти интегралы:
1.
2.
3.
4.
5.
|
6.
7.
8.
9.
10.
|
Вычислить несобственные интегралы или доказать их расходимость:
11.
|
12.
|
Найти площадь фигуры, ограниченной линиями:
13.
|
14.
|
Вычислить длину дуги, заданной уравнением:
15.
|
16.
|
17. Изменить порядок интегрирования в двойном интеграле:
18. Найти площадь поверхности цилиндра
![]() ,
содержащуюся между плоскостями
,
содержащуюся между плоскостями
![]() .
.
19. Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями: .
20. Найти массу цилиндра
![]() ,
если плотность в любой его точке
пропорциональна квадрату расстояния
этой точки от оси цилиндра.
,
если плотность в любой его точке
пропорциональна квадрату расстояния
этой точки от оси цилиндра.
21. Найти общее решение дифференциального уравнения:
1)
![]() ;
;
2)
![]() .
.
Вариант – 6
Найти интегралы:
1.
2.
3.
4.
5.
|
6.
7.
8.
9.
10.
|
Вычислить несобственные интегралы или доказать их расходимость:
11.
|
12.
|
Найти площадь фигуры, ограниченной линиями:
13.
|
14.
|
Вычислить длину дуги, заданной уравнением:
15.
|
16.
|