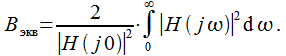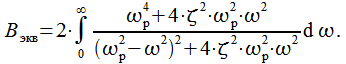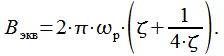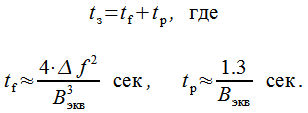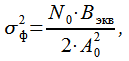Эквивалентная шумовая полоса контура фапч
Для
анализа качества работы контура ФАПЧ
при воздействии аддитивного белого
гауссова шума (AWGN) на входе используют
понятие эквивалентной шумовой полосы
,
определяемой выражением:
|
(25) |
Поясним физический и геометрический смысл эквивалентной шумовой полосы.
Пусть
на входе нашего контура ФАПЧ, который
по сути фильтр с передаточной
характеристикой
действует
AWGN со спектральной плотностью мощности
(СПМ)
.
При прохождении шума через наш фильтр
он изменит свои характеристики и на
выходе будет иметь дисперсию равную
.
Поскольку АЧХ фильтра может сильно
меняться в зависимости от параметров,
то и дисперсия шума на выходе тоже будет
меняться, хотя полоса пропускания
фильтра по уровню -3 дБ остается постоянной,
как и спектральная плотность мощности
шума на входе
.
В нашем случае при фиксированной
резонансной частоте мы можем менять
демпинг фактор
и
получать различные АЧХ при одной полосе
контура ФАПЧ по уровню -3 дБ. Но мы знаем,
что если взять идеальный ФНЧ, то при
фиксированной СПМ
шума
на входе фильтра, дисперсия шума на
выходе будет зависеть только от полосы
идеального ФНЧ. Таким образом эквивалентная
шумовая полоса фильтра
показывает
какую двустороннюю полосу идеального
ФНЧ надо взять, чтобы получить такую же
дисперсию на выходе
,
что и при прохождении через наш фильтр.
В этом физический смысл эквивалентной
шумовой полосы.
Рассмотрим теперь геометрическую трактовку, для этого обратим внимание на рисунок 8.
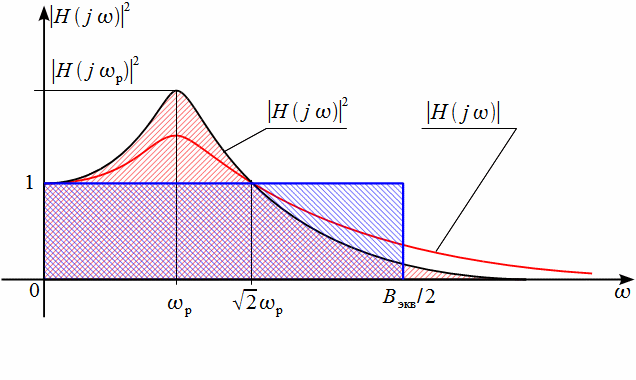Рисунок
8: Геометрическая трактовка эквивалентной
шумовой полосы
На
рисунке 8 красным графиком показана АЧХ
контура ФАПЧ
.
Возводя
в
квадрат получим квадрат АЧХ контура
ФАПЧ
,
площадь под которым заштрихована
красным. Синим показан идеальный ФНЧ,
площадь под квадратом АЧХ которого
(синяя штриховка) равна площади под
квадратом АЧХ контура ФАПЧ. Основание
этого прямоугольника есть половина
эквивалентной шумовой полосы (так как
мы рассмотрели только в одну сторону
положительных частот). В этом геометрическая
трактовка эквивалентной шумовой полосы.
Для расчета эквивалентной шумовой полосы необходимо вычислить интеграл:
|
(26) |
Интеграл можно вычислить численно, или аналитически. Мы не будем этим заниматься, а приведем следующую формулу для эквивалентной шумовой полосы [N1]:
|
(27) |
Интересующийся читатель может самостоятельно проверить результаты расчета эквивалентной шумовой полосы по формулам (26) и (27).
Динамические характеристики контура фапч
Пусть
контур ФАПЧ производит захват
синусоидального сигнала амплитуды
при
начальном частотном рассогласовании
в
условиях действия аддитивного белого
гауссова шума AWGN со спектральной
плотностью мощности
.
В [N1] приведены формулы для оценки поведения контура ФАПЧ при захвате и сопровождении этого сигнала.
Время
захвата
данного
сигнала складывается из захвата по
частоте
и
по фазе
:
|
(28) |
В выражении (28) эквивалентная шумовая полоса выражена в герцах.
Максимальное
частотное рассогласование
,
при котором возможен захват сигнала
должно быть:
|
(29) |
где – демпинг фактор, а эквивалентная шумовая полоса выражена в герцах.
Дисперсия шума оценки фазы на выходе контура ФАПЧ (фазовый шум):
|
(30) |
–
эквивалентная
шумовая полоса (двусторонняя в Гц),
–
амплитуда сигнала в вольтах,
–
СПМ шума имеет размерность Вт/Гц. Таким
образом
–
безразмерная величина.
Выводы
В данной статье мы рассмотрели принцип работы и основные свойства контура ФАПЧ. Были введены понятия статической и астатической ошибки следящей системы, а также порядок астатизма контура ФАПЧ. Установлено, что для сопровождения сигнала по частоте и по фазе требуется контур ФАПЧ 2-го порядка астатизма. Также была получена передаточная характеристика контура ФАПЧ 2-го порядка и рассмотрены ее основные характеристики. Было введено понятие эквивалентной шумовой полосы, и приведена формула ее расчета для контура ФАПЧ 2-го порядка. Кроме того приведены выражения для расчета основных динамических характеристик контура ФАПЧ. В следующей статье мы рассмотрим цифровой контур ФАПЧ и его основные свойства, а также приведем пример моделирования цифрового контура ФАПЧ.