
- •Контур фазовой автоподстройки частоты и его основные свойства
- •Анализ структурной схемы контура фапч
- •Статические и астатические ошибки при работе контура фапч. Порядок астатизма
- •Линеаризованная модель контура фапч
- •Эквивалентная шумовая полоса контура фапч
- •Динамические характеристики контура фапч
Линеаризованная модель контура фапч
Построим
модель контура ФАПЧ, а также рассмотрим
его передаточную характеристику
![]() .
Для начала вспомним, что ГУН интегрирует
сигнал ошибки
,
согласно (2), значит его передаточная
характеристика равна
.
Для начала вспомним, что ГУН интегрирует
сигнал ошибки
,
согласно (2), значит его передаточная
характеристика равна
![]() ,
вместе с тем сам сигнал ошибки выражается
как синус разности фаз согласно (4). Тогда
можно представить модель контура ФАПЧ
как это показано на рисунке 4.
,
вместе с тем сам сигнал ошибки выражается
как синус разности фаз согласно (4). Тогда
можно представить модель контура ФАПЧ
как это показано на рисунке 4.
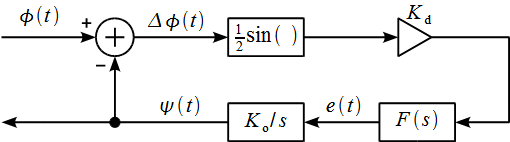 Рисунок
4: Модель контура ФАПЧ
Рисунок
4: Модель контура ФАПЧ
В
модель на рисунке 4 входит нелинейный
элемент вычисляющий синус разности фаз
принятого и опорного колебания, что
существенно затрудняет аналитический
анализ передаточной характеристики
контура ФАПЧ. Однако можно обратить
внимание, что в установившемся режиме
слежения за фазой когда
![]() стремится
сравняться с
,
их разность стремится к нулю, т.е.
стремится
сравняться с
,
их разность стремится к нулю, т.е.
![]() ,
тогда
,
тогда
![]() ,
причем коэффициент 1/2 может быть учтен
в коэффициенте
передаточной
функции ГУН. Таким образом в установившемся
режиме, нелинейный элемент может быть
исключен, и модель контура ФАПЧ показана
на рисунке 5.
,
причем коэффициент 1/2 может быть учтен
в коэффициенте
передаточной
функции ГУН. Таким образом в установившемся
режиме, нелинейный элемент может быть
исключен, и модель контура ФАПЧ показана
на рисунке 5.
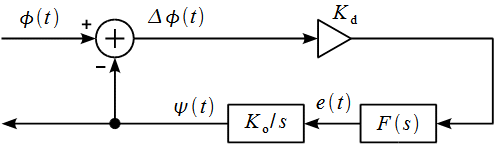 Рисунок
5: Линеаризованная модель контура ФАПЧ
Рисунок
5: Линеаризованная модель контура ФАПЧ
Обозначим
как
![]() и
и
![]() образы
по Лапласу
и
соответственно,
тогда можно записать следующее операторное
уравнение линеаризованного контура
ФАПЧ:
образы
по Лапласу
и
соответственно,
тогда можно записать следующее операторное
уравнение линеаризованного контура
ФАПЧ:
|
(10) |
Раскроем скобки:
|
(11) |
откуда можно выразить передаточную характеристику контура ФАПЧ:
|
(12) |
До текущего момента мы не обсуждали свойства передаточной характеристики петлевого фильтра , однако мы говорили, что нам требуется порядок астатизма контура равный двум, а значит должна содержать полиномы второй степени. Таким образом должна иметь первый порядок. Зададим в виде:
|
(13) |
где
![]() и
и
![]() –
пропорциональный и интегральный
коэффициенты. Сигнал ошибки в этом
случае
можно
выразить, если вспомнить, что
–
пропорциональный и интегральный
коэффициенты. Сигнал ошибки в этом
случае
можно
выразить, если вспомнить, что
![]() в
операторном виде соответствует
интегратору, тогда:
в
операторном виде соответствует
интегратору, тогда:
|
(14) |
Подставив (13) в (12) получим передаточную характеристику линеаризованного контура ФАПЧ:
|
(15) |
Для упрощения введем следующие обозначения:
|
(16) |
тогда
|
(17) |
Получили,
что линеаризованный контур ФАПЧ
представляет собой фильтр второго
порядка с резонансной частотой
![]() и
коэффициентом затухания (демпинг
фактором damping factor)
и
коэффициентом затухания (демпинг
фактором damping factor)
![]()
Комплексный коэффициент передачи линеаризованного контура ФАПЧ равен:
|
(18) |
АЧХ линеаризованного контура ФАПЧ равна:
|
(19) |
Рассмотрим основные частотные соотношения в линеаризованном контуре ФАПЧ.
При
![]() АЧХ
линеаризованного контура ФАПЧ равна
АЧХ
линеаризованного контура ФАПЧ равна
![]() .
.
При
![]() получим:
получим:
|
(20) |
На
резонансной частоте АЧХ линеаризованного
контура ФАПЧ всегда больше единицы,
причем при устремлении
к
нулю
![]() стремится
к бесконечности.
стремится
к бесконечности.
При
![]() получим:
получим:
|
(21) |
Таким
образом АЧХ контура ФАПЧ убывает как
![]() (20
дБ/декада).
(20
дБ/декада).
Рассмотрим
частоту при которых
![]() .
Для этого необходимо решить уравнение
(19) при
относительно
частоты
.
Для этого необходимо решить уравнение
(19) при
относительно
частоты
![]() .
Возводя в квадрат и перенося знаменатель
в левую часть получим:
.
Возводя в квадрат и перенося знаменатель
в левую часть получим:
|
(22) |
Раскрывая скобки и приводя подобные получим:
|
(23) |
Основные частотные соотношения АЧХ линеаризованного контура ФАПЧ показаны на рисунке 6.
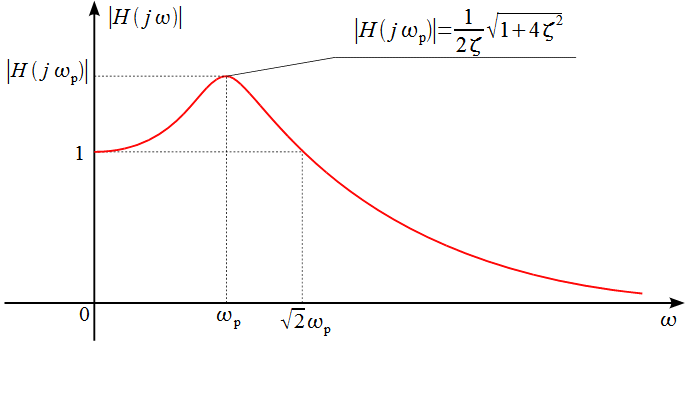 Рисунок
6: Основные частотные соотношения АЧХ
линеаризованного контура ФАПЧ
Рисунок
6: Основные частотные соотношения АЧХ
линеаризованного контура ФАПЧ
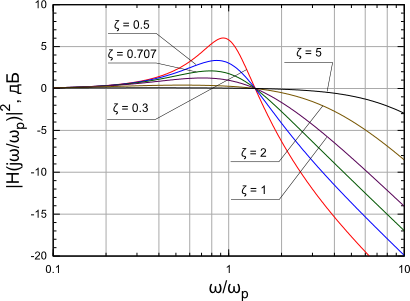
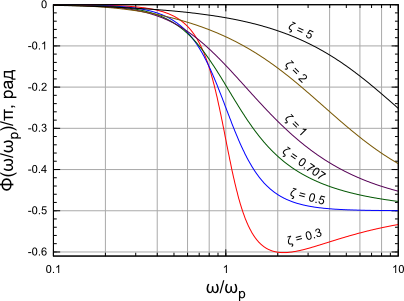
На рисунке 7 показаны логарифмические АЧХ
|
(24) |
и ФЧХ линеаризованного контура ФАПЧ, от частоты, нормированной к резонансной частоте при различных параметрах .
|
|
Рисунок 7: Логарифмические АЧХ и ФЧХ

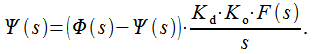
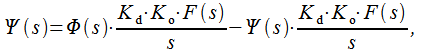
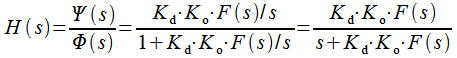
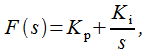
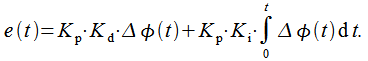
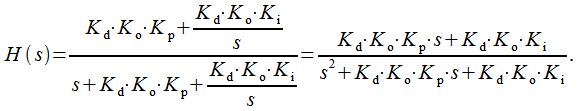
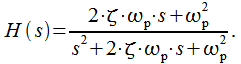
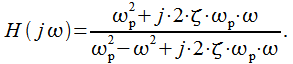
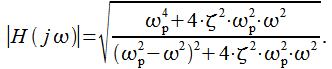
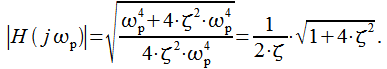
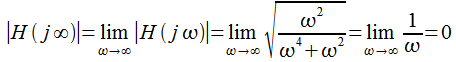
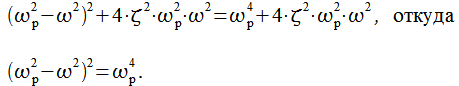
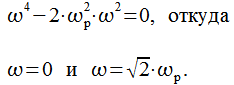
 Для
просмотра SVG графики Вам необходимо
обновить браузер
Для
просмотра SVG графики Вам необходимо
обновить браузер
 Для
просмотра SVG графики Вам необходимо
обновить браузер
Для
просмотра SVG графики Вам необходимо
обновить браузер